每一个维度上的值都属于一个高斯分布, 不同维度之间有相互联系(通过kernel/协方差来表示). 一个数据就是此高斯过程的一次采样.

高斯过程也可以理解为插值:
- 对于函数$f(x)$, 每一次从不同$x$处观察$f(x)$都可以作为一个随机变量来看待, 它们都服从和一个$x$无关的高斯噪声分布.
- 对于任意两个$x, x'$, 我们认为$x$和$x'$的距离决定了他们之间的相关性.
从而, 例如
我们从最简单最常见的一元高斯分布开始,其概率密度函数为 $$ p(x) = \frac{1}{\sigma\sqrt{2\pi}}\mathrm{exp}(-\frac{(x-\mu)^2}{2\sigma^2}) \tag{1} $$
其中
从一元高斯分布推广到多元高斯分布,假设各维度之间相互独立
其中
则
代入上式得到
$$
p(\boldsymbol{x}) = (2\pi)^{-\frac{n}{2}}|K|^{-\frac{1}{2}}\mathrm{exp}\left( -\frac{1}{2}(\boldsymbol{x-\mu})^TK^{-1}(\boldsymbol{x-\mu}) \right) \tag{3}
$$
其中 $ \boldsymbol{\mu} \in \mathbb{R}^n $ 是均值向量, $ K \in \mathbb{R}^{n \times n} $ 为协方差矩阵,由于我们假设了各维度直接相互独立,因此 $ K $ 是一个对角矩阵。在各维度变量相关时,上式的形式仍然一致,但此时协方差矩阵
在多元高斯分布的基础上进一步扩展,假设有无限多维呢?我们用一个例子来展示这个扩展的过程(来源:MLSS 2012: J. Cunningham - Gaussian Processes for Machine Learning)。
假设我们在周一到周四每天的 7:00 测试了 4 次心率,如图中 4 个点,可能的高斯分布如图所示(高瘦的曲线)。这是一个一元高斯分布,只有每天 7: 00 心率这个维度。
现在考虑不仅在每天的 7: 00 测心率,在 8:00 时也进行测量,这个时候变成两个维度(二元高斯分布),如图所示
如果我们在每天的无限个时间点都进行测量,则变成了下图的情况。注意下图中把测量时间作为横轴,则每个颜色的一条线代表一个(无限个时间点的测量)无限维的采样。当对无限维进行采样得到无限多个点时,其实可以理解为对函数进行采样。
当从函数的视角去看待采样,理解了每次采样无限维相当于采样一个函数之后,原本的概率密度函数不再是点的分布 ,而变成了函数的分布。这个无限元高斯分布即称为高斯过程。高斯过程正式地定义为:对于所有
都服从多元高斯分布,则称
这里
核函数是一个高斯过程的核心,核函数决定了一个高斯过程的性质。核函数在高斯过程中起的作用是生成一个协方差矩阵(相关系数矩阵),衡量任意两个点之间的“距离”。最常用的一个核函数为高斯核函数,也成为径向基函数 RBF。其基本形式如下。其中 $ \sigma$和
以上高斯核函数的 python 实现如下
import numpy as np
def gaussian_kernel(x1, x2, l=1.0, sigma_f=1.0):
"""Easy to understand but inefficient."""
m, n = x1.shape[0], x2.shape[0]
dist_matrix = np.zeros((m, n), dtype=float)
for i in range(m):
for j in range(n):
dist_matrix[i][j] = np.sum((x1[i] - x2[j]) ** 2)
return sigma_f ** 2 * np.exp(- 0.5 / l ** 2 * dist_matrix)
def gaussian_kernel_vectorization(x1, x2, l=1.0, sigma_f=1.0):
"""More efficient approach."""
dist_matrix = np.sum(x1**2, 1).reshape(-1, 1) + np.sum(x2**2, 1) - 2 * np.dot(x1, x2.T)
return sigma_f ** 2 * np.exp(-0.5 / l ** 2 * dist_matrix)
x = np.array([700, 800, 1029]).reshape(-1, 1)
print(gaussian_kernel_vectorization(x, x, l=500, sigma=10))输出的协方差矩阵为
[[100. 98.02 80.53]
[ 98.02 100. 90.04]
[ 80.53 90.04 100. ]]
下图是高斯过程的可视化,其中蓝线是高斯过程的均值,浅蓝色区域 95% 置信区间(由协方差矩阵的对角线得到),每条虚线代表一个函数采样(这里用了 100 维模拟连续无限维)。左上角第一幅图是高斯过程的先验(这里用了零均值作为先验),后面几幅图展示了当观测到新的数据点的时候,高斯过程如何更新自身的均值函数和协方差函数。
接下来我们用公式推导上图的过程。将高斯过程的先验表示为$f(\boldsymbol{x}) \sim \mathcal{N}(\boldsymbol{\mu}{f}, K{ff})$,对应左上角第一幅图,如果现在我们观测到一些数据 $ (\boldsymbol{x^{}}, \boldsymbol{y^{}}) $ ,并且假设 $ \boldsymbol{y^{}} $ 与 $ f(\boldsymbol{x}) $ 服从联合高斯分布 $$ \begin{bmatrix} f(\boldsymbol{x})\ \boldsymbol{y^{}}\ \end{bmatrix} \sim \mathcal{N} \left( \begin{bmatrix} \boldsymbol{\mu_f}\ \boldsymbol{\mu_y}\ \end{bmatrix}, \begin{bmatrix} K_{ff} & K_{fy}\ K_{fy}^T & K_{yy}\ \end{bmatrix} \right) $$
其中 $ K_{ff} = \kappa(\boldsymbol{x}, \boldsymbol{x}) $ ,$$ K_{fy}=\kappa(\boldsymbol{x}, \boldsymbol{x^{}}) $,$ K_{yy} = \kappa(\boldsymbol{x^{}}, \boldsymbol{x^{*}}) $ ,则有 $$ f \sim \mathcal{N}(K_{fy}^{T}K_{ff}^{-1}\boldsymbol{y}+\boldsymbol{\mu_f},K_{yy}-K_{fy}^{T}K_{ff}^{-1}K_{fy}) \tag{5} $$
公式(5)表明了给定数据$(\boldsymbol{x^{}}, \boldsymbol{y^{}})$ 之后函数的分布 $ f $ 仍然是一个高斯过程,具体的推导可见 Gaussian Processes for Machine Learning。这个式子可以看出一些有趣的性质,均值
上式其实就是高斯过程回归的基本公式,首先有一个高斯过程先验分布,观测到一些数据(机器学习中的训练数据),基于先验和一定的假设(联合高斯分布)计算得到高斯过程后验分布的均值和协方差。
考虑代码实现一个高斯过程回归,API 接口风格采用 sciki-learn fit-predict 风格。由于高斯过程回归是一种非参数化的方法,每次的 inference 都需要利用所有的训练数据进行计算得到结果,因此并没有一个显式的训练模型参数的过程,所以 fit 方法只需要将训练数据记录下来,实际的 inference 在 predict 方法中进行。Python 代码如下
from scipy.optimize import minimize
class GPR:
def __init__(self, optimize=True):
self.is_fit = False
self.train_X, self.train_y = None, None
self.params = {"l": 0.5, "sigma_f": 0.2}
self.optimize = optimize
def fit(self, X, y):
# store train data
self.train_X = np.asarray(X)
self.train_y = np.asarray(y)
self.is_fit = True
def predict(self, X):
if not self.is_fit:
print("GPR Model not fit yet.")
return
X = np.asarray(X)
Kff = self.kernel(self.train_X, self.train_X) # (N, N)
Kyy = self.kernel(X, X) # (k, k)
Kfy = self.kernel(self.train_X, X) # (N, k)
Kff_inv = np.linalg.inv(Kff + 1e-8 * np.eye(len(self.train_X))) # (N, N)
mu = Kfy.T.dot(Kff_inv).dot(self.train_y)
cov = Kyy - Kfy.T.dot(Kff_inv).dot(Kfy)
return mu, cov
def kernel(self, x1, x2):
dist_matrix = np.sum(x1**2, 1).reshape(-1, 1) + np.sum(x2**2, 1) - 2 * np.dot(x1, x2.T)
return self.params["sigma_f"] ** 2 * np.exp(-0.5 / self.params["l"] ** 2 * dist_matrix)def y(x, noise_sigma=0.0):
x = np.asarray(x)
y = np.cos(x) + np.random.normal(0, noise_sigma, size=x.shape)
return y.tolist()
train_X = np.array([3, 1, 4, 5, 9]).reshape(-1, 1)
train_y = y(train_X, noise_sigma=1e-4)
test_X = np.arange(0, 10, 0.1).reshape(-1, 1)
gpr = GPR()
gpr.fit(train_X, train_y)
mu, cov = gpr.predict(test_X)
test_y = mu.ravel()
uncertainty = 1.96 * np.sqrt(np.diag(cov))
plt.figure()
plt.title("l=%.2f sigma_f=%.2f" % (gpr.params["l"], gpr.params["sigma_f"]))
plt.fill_between(test_X.ravel(), test_y + uncertainty, test_y - uncertainty, alpha=0.1)
plt.plot(test_X, test_y, label="predict")
plt.scatter(train_X, train_y, label="train", c="red", marker="x")
plt.legend()结果如下图,红点是训练数据,蓝线是预测值,浅蓝色区域是 95% 置信区间。真实的函数是一个 cosine 函数,可以看到在训练数据点较为密集的地方,模型预测的不确定性较低,而在训练数据点比较稀疏的区域,模型预测不确定性较高。
上文提到高斯过程是一种非参数模型,没有训练模型参数的过程,一旦核函数、训练数据给定,则模型就被唯一地确定下来。但是核函数本身是有参数的,比如高斯核的参数 $ \sigma $ 和 $ l $ ,我们称为这种参数为模型的超参数(类似于 k-NN 模型中 k 的取值)。
核函数本质上决定了样本点相似性的度量方法,进行影响到了整个函数的概率分布的形状。上面的高斯过程回归的例子中使用了 $ \sigma=0.2 $ 和 $ l=0.5 $ 的超参数,我们可以选取不同的超参数看看回归出来的效果。
从上图可以看出,$ l $ 越大函数更加平滑,同时训练数据点之间的预测方差更小,反之 $ l $ 越小则函数倾向于更加“曲折”,训练数据点之间的预测方差更大;$ \sigma $ 则直接控制方差大小,$ \sigma $ 越大方差越大,反之亦然。
如何选择最优的核函数参数 $ \sigma $ 和 $ l $ 呢?答案最大化在这两个超参数下 $ \boldsymbol{y} $ 出现的概率,通过最大化边缘对数似然(Marginal Log-likelihood)来找到最优的参数,边缘对数似然表示为 $$ \mathrm{log}\ p(\boldsymbol{y}|\sigma, l) = \mathrm{log} \ \mathcal{N}(\boldsymbol{0}, K_{yy}(\sigma, l)) = -\frac{1}{2}\boldsymbol{y}^T K_{yy}^{-1}\boldsymbol{y} - \frac{1}{2}\mathrm{log}\ |K_{yy}| - \frac{N}{2}\mathrm{log} \ (2\pi) \tag{6} $$ 具体的实现中,我们在 fit 方法中增加超参数优化这部分的代码,最小化负边缘对数似然。
from scipy.optimize import minimize
class GPR:
def __init__(self, optimize=True):
self.is_fit = False
self.train_X, self.train_y = None, None
self.params = {"l": 0.5, "sigma_f": 0.2}
self.optimize = optimize
def fit(self, X, y):
# store train data
self.train_X = np.asarray(X)
self.train_y = np.asarray(y)
# hyper parameters optimization
def negative_log_likelihood_loss(params):
self.params["l"], self.params["sigma_f"] = params[0], params[1]
Kyy = self.kernel(self.train_X, self.train_X) + 1e-8 * np.eye(len(self.train_X))
return 0.5 * self.train_y.T.dot(np.linalg.inv(Kyy)).dot(self.train_y) + 0.5 * np.linalg.slogdet(Kyy)[1] + 0.5 * len(self.train_X) * np.log(2 * np.pi)
if self.optimize:
res = minimize(negative_log_likelihood_loss, [self.params["l"], self.params["sigma_f"]],
bounds=((1e-4, 1e4), (1e-4, 1e4)),
method='L-BFGS-B')
self.params["l"], self.params["sigma_f"] = res.x[0], res.x[1]
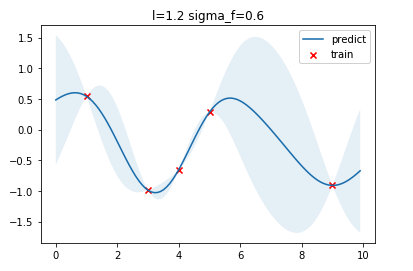
self.is_fit = True将训练、优化得到的超参数、预测结果可视化如下图,可以看到最优的 $ l=1.2
这里用 scikit-learn 的 GaussianProcessRegressor 接口进行对比
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import ConstantKernel, RBF
# fit GPR
kernel = ConstantKernel(constant_value=0.2, constant_value_bounds=(1e-4, 1e4)) * RBF(length_scale=0.5, length_scale_bounds=(1e-4, 1e4))
gpr = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=2)
gpr.fit(train_X, train_y)
mu, cov = gpr.predict(test_X, return_cov=True)
test_y = mu.ravel()
uncertainty = 1.96 * np.sqrt(np.diag(cov))
# plotting
plt.figure()
plt.title("l=%.1f sigma_f=%.1f" % (gpr.kernel_.k2.length_scale, gpr.kernel_.k1.constant_value))
plt.fill_between(test_X.ravel(), test_y + uncertainty, test_y - uncertainty, alpha=0.1)
plt.plot(test_X, test_y, label="predict")
plt.scatter(train_X, train_y, label="train", c="red", marker="x")
plt.legend()得到结果为 $ l=1.2, \sigma_f=0.6 $,这个与我们实现的优化得到的超参数有一点点不同,可能是实现的细节有所不同导致。
我们上面讨论的训练数据都是一维的,高斯过程直接可以扩展于多维输入的情况,直接将输入维度增加即可。
def y_2d(x, noise_sigma=0.0):
x = np.asarray(x)
y = np.sin(0.5 * np.linalg.norm(x, axis=1))
y += np.random.normal(0, noise_sigma, size=y.shape)
return y
train_X = np.random.uniform(-4, 4, (100, 2)).tolist()
train_y = y_2d(train_X, noise_sigma=1e-4)
test_d1 = np.arange(-5, 5, 0.2)
test_d2 = np.arange(-5, 5, 0.2)
test_d1, test_d2 = np.meshgrid(test_d1, test_d2)
test_X = [[d1, d2] for d1, d2 in zip(test_d1.ravel(), test_d2.ravel())]
gpr = GPR(optimize=True)
gpr.fit(train_X, train_y)
mu, cov = gpr.predict(test_X)
z = mu.reshape(test_d1.shape)
fig = plt.figure(figsize=(7, 5))
ax = Axes3D(fig)
ax.plot_surface(test_d1, test_d2, z, cmap=cm.coolwarm, linewidth=0, alpha=0.2, antialiased=False)
ax.scatter(np.asarray(train_X)[:,0], np.asarray(train_X)[:,1], train_y, c=train_y, cmap=cm.coolwarm)
ax.contourf(test_d1, test_d2, z, zdir='z', offset=0, cmap=cm.coolwarm, alpha=0.6)
ax.set_title("l=%.2f sigma_f=%.2f" % (gpr.params["l"], gpr.params["sigma_f"]))下面是一个二维输入数据的告你过程回归,左图是没有经过超参优化的拟合效果,右图是经过超参优化的拟合效果。
以上完整的的代码放在 toys/GP。
-
优点
- (采用 RBF 作为协方差函数)具有平滑性质,能够拟合非线性数据
- 高斯过程回归天然支持得到模型关于预测的不确定性(置信区间),直接输出关于预测点值的概率分布
- 通过最大化边缘似然这一简洁的方式,高斯过程回归可以在不需要交叉验证的情况下给出比较好的正则化效果
-
缺点
- 高斯过程是一个非参数模型,每次的 inference 都需要对所有的数据点进行(矩阵求逆)。对于没有经过任何优化的高斯过程回归,n个样本点时间复杂度大概是
$\mathcal{O}(n^3)$ ,空间复杂度是$\mathcal{O}(n^2)$ ,在数据量大的时候高斯过程变得 intractable - 高斯过程回归中,先验是一个高斯过程,likelihood 也是高斯的,因此得到的后验仍是高斯过程。在 likelihood 不服从高斯分布的问题中(如分类),需要对得到的后验进行 approximate 使其仍为高斯过程
- RBF 是最常用的协方差函数,但在实际中通常需要根据问题和数据的性质选择恰当的协方差函数
- 高斯过程是一个非参数模型,每次的 inference 都需要对所有的数据点进行(矩阵求逆)。对于没有经过任何优化的高斯过程回归,n个样本点时间复杂度大概是
这里简单介绍: 利用高斯过程分离地面, 该论文中的高斯过程的使用. 我们知道, 对于平坦的地面length-scal
这里, M是扇区的数量, N是每个扇区bin的数量,
在wavelib的实现中, 并没有为每一个$r_i$单独计算$l_i$, 而是将$l$作为一个输入参数. 当然, hyper-parameters和$\sigma_n^2$, 也作为输入参数. 该代码基本实现该算法, 其中的INSAC(Incremental Sample Consensus)值得借鉴.
简化后的公式:
$$
\begin{aligned}
k(r_i, r_j) &= \sigma_f^2 \exp(-\frac{(r_i - r_j)^2}{2l^2})\
K &= k + \sigma_n^2 \mathbf{I}
\end{aligned}
$$
各参数的直观理解:
-
参考了..根据梯度选取种子点
-
insac过程中, 判断点是否是inlier的方法优化 原实现认为
$\frac{|y_{test} - y_{predict}|}{\sigma} < th$ 则为inlier, 由上面的图可以看出, 当距离越远,$\sigma$ 越大(不确定度也越大), 这样的判断是不准确的. 原方法代码:double met = (sig_points[k].height - f_s(k)) / (sqrt(this->params.p_sn + vf * vf)); if (vf < this->params.p_tmodel & std::abs(met) < this->params.p_tdata) { // we have an inlier! ... }在进行一次拟合后, 我们得到了测试点的预测分布$\mathcal{N}(y_{predict}, \sigma_{predict})$, 按照此分布, 我们要求在
$[y_{test} - th, y_{test}+th_{height}]$ 区间内的概率超过$th_{probility}$ . 这里$th_{height} = 0.1, th_{probility}=0.8$, 即 我们有80%的概率, 真实的地面高度与测试值相差在0.1米以内.简化积分的计算, 使用 $(P(y_{test} - th) + P(y_{test} + th))0.5th$来近似.
-
TODO 超参数优化
Code:
- 高斯过程 Gaussian Processes 原理、可视化及代码实现
- 通俗易懂地介绍Gaussian Process
- 高斯过程的基本原理
- 机器学习中的高斯过程
- Gaussian Process 理论
- Matlab GP example 代码
- GP Ground Segmentation
- GP Ground Segmentation Code Wavelib
- Carl Edward Rasmussen - Gaussian Processes for Machine Learning
- MLSS 2012 J. Cunningham - Gaussian Processes for Machine Learning
- Martin Krasser's blog- Gaussian Processes
- scikit-learn GaussianProcessRegressor