cpp_matrix: C++ implementation of a matrix class and linear solvers

(For code description see bottom)

This project's purpose was to analyze the different scaling patterns of commonly used Linear solvers. The algorithms implemented here are: LU, QR (implicit and explicit), SD, CG, CG with Jacobi pre-conditioning, Sucessive-overrelaxation, Jacobi, Gauss-Seidel.

Linear Systems

What are they?

Linear systems have the shape Ax = b with a known matrix A and known vector b. Essentially all we're trying to do is x=A\b, in Matlab notation. Note also that these solvers can be used for finding an x that minimizes || Ax - b ||. This is done by solving the symmetric system A'Ax = A'b (note however that the condition number will be squared).

Quick overview of when which solver can be used.

Any A

LU, QR, SD, (if you take the squared system: CG)

Symmetric A

LU, QR, SD, CG.

Strictly-row/column-diagonally-dominant (SRDD) A

LU, QR, SD, CG, Sucessive-overrelaxation (includes Jacobi and Gauss-Seidel)

Generating random linear systems

Steps for generating random matrices of size N with desired condition numbers κ:

1. We generate random matrix Q of size NxN
2. We orthonormalize the columns via modified Gram-Schmidt
3. We let D = diag(linspace(1,...,κ))
4. A = QD or if we want a symmetric system: A = QDQ'
5. Generate random vector x and let b = Ax.

Steps for generating SRDD matrices with size N and approximately κ = 2N

1. Generate random matrix A of size NxN
2. Set diagonal entries of A to linspace(N,...,2N)
3. Generate random vector x and let b = Ax. By Gershogorin discs the matrix has approximately the eigenvalues (N,...,2N) and thus κ = 2.

Results

Same condition number κ, varying size N, non-symmetric A

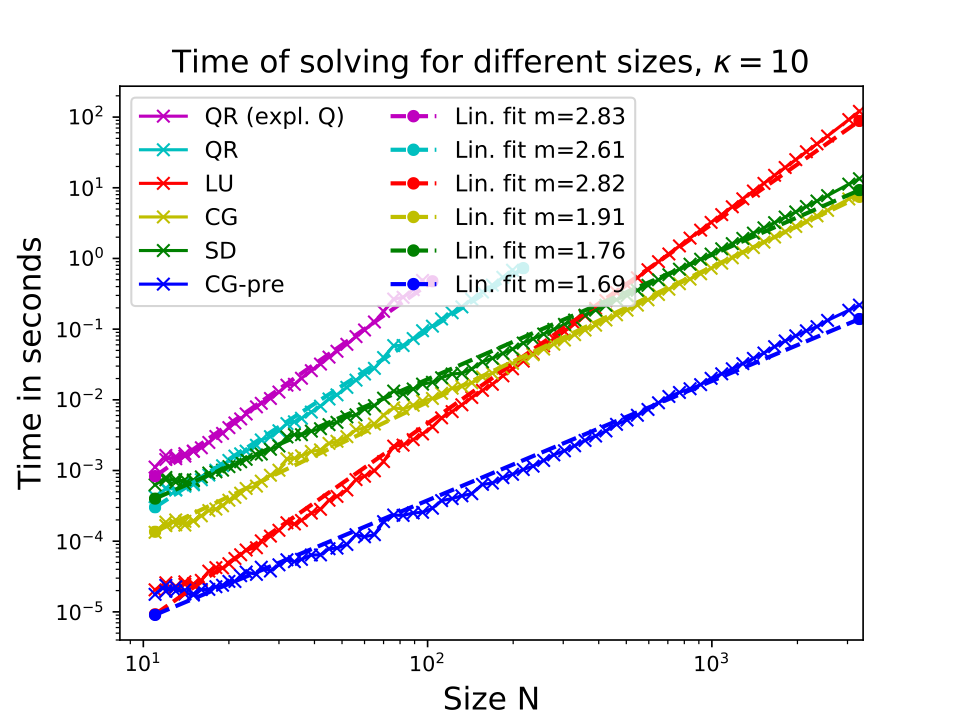
In the above figure we use the normal system for the CG solvers.

Same condition number κ, varying size N, symmetric A

Same size N, varying condition number κ, symmetric A

SRDD with condition number κ=2 and varying size N

Some results

• symmetric matrices with low condition number are easiest to solve
• iterative methods can outperform decomposition methods even for modest problem sizes
• the algorithms scale very differently, though consistently faster then their theoretical prediction
• pre-conditioning improves convergences of the CG algorithm
• which algorithm is the fastest depends crucially on the problem size and the condition number, though CG-pre and LU among the fastest implemented here

Critical remarks

• Definitely easier to implement in Matlab, Python.. there are definitely still some bugs in my code
• Matrices were too easy for my solvers in some cases by construction (CG with pre-conditioning converges in 1-step for A = QDQ')
• Writing everything in C++ was instructive but one should really use proper templates like Eigen

Code

• vary_N.cpp: implements the above procedure for symmetric A system with 10 iterations at every size. Sizes grow exponentially.
• vary_kappa.cpp: same as vary_N except that now we vary κ at every iteration and keep N = 100
• SRDD.cpp: Generates SRDD matrix as above and solves it, also 10 iterations at every size that grows exponentially.
• Matrix.cpp: Includes the matrix class and all methods and the solvers
• Vector.cpp: A vector class, as from introductory C++ course of Joe Pit-Francis