dagilim-olculeri.md

Dağılım Ölçüleri

İstatistik konuları ve daha fazlası yeni sitemize taşınmıştır.

Veri Bilimi ve Veri Analizi | İstatistik için tıklayınız.

Yayılım ya da Değişkenlik Ölçüleri olarak da adlandırılan Dağılım Ölçüleri (measure of dispersion)¹ veri birimlerinin genelinin ortalamadan ne kadar uzak ya da ortalamaya ne kadar yakın olduğunu gösteren temel ölçülerden biridir. Merkezî eğilim ölçülerinden olan aritmetik ortalama, mod ve medyan her zaman serinin heterojen ya da homojen dağıldığını göstermemektedir. Bu sebeple serinin dağılımı hakkında merkezî eğilim ölçülerine göre daha anlamlı sonuçlar veren standart sapma ve değişim katsayısı gibi dağılım ölçüleri kullanılır.

Yukarıdaki grafikte kişi başına günlük harcama tutarlarını gösteren iki gruba ait veriler dağılım grafiğinde gösterilmiştir. İki grubun da kişi başına günlük ortalama harcaması 100 TL olmasına rağmen kırmızı grubun standart sapması² 10 TL iken mavi grubun standart sapması 50 TL’dir. Bu sebeple iki grubun da aynı karakteristik özelliklere sahip olduğunu söyleyemeyiz. İki grubu birbiri ile karşılaştırmak için dağılım ölçülerinden yararlanırız.

Dağılım Ölçüleri

İstatistik konuları ve daha fazlası yeni sitemize taşınmıştır.

Veri Bilimi ve Veri Analizi | İstatistik için tıklayınız.

Değişim Aralığı (Range)

Kartiller Arası Fark (IQR)

Ortalama Mutlak Sapma (MAD)

Standart Sapma (SD) ve Varyans

Sheppard Düzeltmesi

Standart Hata (SE)

Değişim Katsayısı (CV)

SPSS'te Dağılım Ölçüleri

Kutu Diyagramı (Box-Plot)

SPSS'te Kutu Diyagramı

Değişim Aralığı

Değişim Aralığı ya da Ranj (Range), en kolay anlaşılan dağılım ölçüsü olmakla birlikte uygulaması da en kolay yayılım ölçüsüdür. Aykırı değerlerden hemen etkilenir ve açık uçlu dağılımlar için hesaplanamaz.

Anakütle Değişim Aralığı

Tüm Serilerde

$$ R = X_{max} - X_{min} $$

Örneklem Değişim Aralığı

Tüm Serilerde

$$ R = x_{max} - x_{min} $$

R: Range, Değişim Aralığı, X_max: Serinin en büyük değeri, X_min: Serinin en küçük değeri

Excel’de değişim aralığını bulmak için =MAK()-MİN() formülünü kullanabiliriz.

Uygulama: Bir sınıftan seçilen 10 öğrencinin sınav notları aşağıda verilmiştir.

$$ x = 40, 55, 60, 60, 65, 70, 75, 80, 85, 90 $$

Notların değişim aralığını bulunuz.

$$ R = x_{max} - x_{min} = 90 - 40 = 50 $$

Serinin en büyük değeri 90, en küçük değeri 40’tır. İki değer arasındaki mesafe (range), değişim aralığını vermektedir.

---

İstatistik konuları ve daha fazlası yeni sitemize taşınmıştır.

Veri Bilimi ve Veri Analizi | İstatistik için tıklayınız.

Kartiller Arası Fark (IQR)

Kartiller Arası Fark (Interquartile Range, IQR)³ ya da Çeyrekler Arası Açıklığı serinin %75. dilimine denk gelen Q₃ kartili ve %25. dilime denk gelen Q₁ kartili arasındaki farkı belirtmektedir.

Anakütle ve Örneklem Kartiller Arası Farkı

Tüm Serilerde

$$ IQR = Q_3 - Q_1 $$

Kartiller Arası Fark (IQR) çoğunlukla kutu grafiklerinde⁴ yoğun olarak kullanılmakla birlikte olasılık yoğunluk fonkisyonu ve standart normal dağılım grafiklerinde dağılımın %50’sini oluşturmaktadır.

Excel’de Kartiller Arası Fark almak için =DÖRTTEBİRLİK(seri;3)-DÖRTTEBİRLİK(seri;1) hesaplamasını yapabiliriz.

Uygulama: X₁ = 12, 14, 14, 16, 18, 18, 18, 18, 18, 20, 24 serisinin kartiller arası farkını (IQR'ını) bulunuz.

n: 11’dir. Gözlem sayısı tek sayı olduğu için

$$ Q_1 = { X_{ { N+2 } \over 4 } } = { X_{ { 11+2 } \over 4 } } = X_{3.25} \approx X_3 = 14 $$

$$ Q_3 = { X_{ { 3N+2 } \over 4 } } = { X_{ { 3(11)+2 } \over 4 } } = X_{8.75} \approx X_9 = 18 $$

$$ IQR = Q_3 - Q_1 = 18 - 14 = 4 $$

---

Ortalama Mutlak Sapma (MAD)

Ortalama Mutlak Sapma (Mean Absolute Deviation, MAD), verilerin ortalamadan sapmalarının mutlak değerlerinin ortalamasıdır. Bu dağılım ölçüsünde her gözlemin sapmasına eşit ağırlık tanınır ve standart sapma kadar aykırı değerlerden etkilenmez. Kimi durumlarda ortalama yerine medyan da kullanılabilmektedir.

Anakütle Ortalama Mutlak Sapması

Basit Serilerde

$$ MAD = { { \Sigma|X_i - \mu| } \over N } $$

Frekans Serilerinde

$$ MAD = { { \Sigma f_i|X_i - \mu| } \over \Sigma f_i } $$

Gruplandırılmış Serilerde

$$ MAD = { { \Sigma f_i|m_i - \mu| } \over \Sigma f_i } $$

Örneklem Ortalama Mutlak Sapması

Basit Serilerde

$$ MAD = { { \Sigma|x_i - \bar x| } \over n } $$

Frekans Serilerinde

$$ MAD = { { \Sigma f_i|x_i - \bar x| } \over \Sigma f_i } $$

Gruplandırılmış Serilerde

$$ MAD = { { \Sigma f_i|m_i - \bar x| } \over \Sigma f_i } $$

m: Sınıf Orta Sayısı, f: Frekans

Excel’de ortalama mutlak sapmanın formülü bulunmamaktadır. Buna rağmen mutlak değerleri hesaplarken =MUTLAK() formülünü kullanabiliriz.

Uygulama: Bir sınıftan seçilen 10 öğrencinin sınav notları aşağıda verilmiştir.

$$ x = 40, 55, 60, 60, 65, 70, 75, 80, 85, 90 $$

Notların ortalama mutlak sapmasını (MAD’ini) bulunuz.

Öncelikle aritmetik ortalamayı buluruz.

$$ \bar x = { { \Sigma x_i } \over n } $$

$$ \bar x = { { 40+55+60+60+65+70+75+80+85+90 } \over 10 } = 68 $$

Ardından ortalama mutlak sapmayı (MAD’i) hesaplarız.

$$ MAD = { { \Sigma|x_i - \bar x| } \over n } $$

$$ MAD = { { |40 - 68| + |55 - 68| \ + ... + \ |85 - 68| + |90 - 68| } \over 10 } $$

$$ MAD = { { 23 + 13 + ... +\ 17 + 22 } \over 10 } = 12 \text{ puan} $$

Uygulama: Bir sınıftaki tüm öğrencilerin boy uzunlukları tabloda listelenmiştir.

Boy Uzunluğu	Öğrenci Sayısı
155 cm	1
160 cm	2
165 cm	7
170 cm	16
175 cm	18
180 cm	6
185 cm	4
190 cm	1
Toplam (Σ)	55

Boy uzunluklarının ortalama mutlak sapmasını (MAD’ini) bulunuz.

Öncelikle aritmetik ortalamayı buluruz.

Boy Uzunluğu (Xi)	Öğrenci Sayısı (fi)	Xifi
155 cm	1	155
160 cm	2	320
165 cm	7	1155
170 cm	16	2720
175 cm	18	3150
180 cm	6	1080
185 cm	4	740
190 cm	1	190
Toplam (Σ)	55	9510

$$ \mu = {\Sigma X_i f_i \over N} $$

$$ \mu = {155 + 320 + 1155 + 2720 + 3150 + 180 + 740 + 190 \over 55} = 172.91 \approx 173 \text{ cm} $$

Ardından ortalama mutlak sapmayı (MAD’i) hesaplarız.

Boy Uzunluğu (Xi)	Öğrenci Sayısı (fi)	fi|Xi-µ|
155 cm	1	1|155-173|
160 cm	2	2|160-173|
165 cm	7	7|165-173|
170 cm	16	16|170-173|
175 cm	18	18|175-173|
180 cm	6	6|180-173|
185 cm	4	4|185-173|
190 cm	1	1|190-173|
Toplam (Σ)	55	351

$$ MAD = { { \Sigma f_i|X_i - \mu| } \over \Sigma f_i } = { 351 \over 55 } = 6.38 \approx 6 \text{ cm} $$

Uygulama: Bir sınıftaki tüm öğrencilerin boy uzunlukları tabloda listelenmiştir.

Boy Uzunluğu	Öğrenci Sayısı
150 – 159 cm	4
160 – 169 cm	12
170 – 179 cm	36
180 – 189 cm	8
190 – 200 cm	2
Toplam (Σ)	62

Boy uzunluklarının ortalama mutlak sapmasını (MAD’ini) bulunuz.

Öncelikle ortalamayı buluruz.

Boy Uzunluğu	mi	Öğrenci Sayısı (fi)	mifi
150 – 159 cm	155 cm	4	620
160 – 169 cm	165 cm	12	1980
170 – 179 cm	175 cm	36	6300
180 – 189 cm	185 cm	8	1480
190 – 200 cm	195 cm	2	390
Toplam (Σ)		62	10770

$$ \mu = {\Sigma m_i f_i \over N} $$

$$ \mu = {(155 \times 4) + (165 \times 2) + (175 \times 36) + (185 \times 8) + (195 \times 2) \over 62} = 173.71 \approx 174 \text{ cm} $$

Ardından ortalama mutlak sapmayı (MAD’i) hesaplarız.

Boy Uzunluğu	mi	Öğrenci Sayısı (fi)	fi|mi-µ|
150 – 159 cm	155 cm	4	4|155 – 174|
160 – 169 cm	165 cm	12	12|165 – 174|
170 – 179 cm	175	36	36|175 – 174|
180 – 189 cm	185 cm	8	8|185 – 174|
190 – 200 cm	195 cm	2	2|195 – 174|
Toplam (Σ)		62	350

$$ MAD = { { \Sigma f_i|m_i - \mu| } \over \Sigma f_i } = { 350 \over 62 } = 5.65 \approx 6 \text{ cm} $$

---

Standart Sapma (SD) ve Varyans

Standart Sapma (Standart Deviation, SD, STDEV) gözlem değerlerinin aritmetik ortalamadan sapmalarının kareli ortalamasıdır. Standart sapmanın karesi ise Varyans (Variance, VAR) olarak adlandırılır.

En çok kullanılan ve en önemli dağılım ölçüsüdür. Açık uçlu dağılımlar için hesaplanamaz.

Anakütle için σ (küçük sigma), örneklem için s notasyonu ile gösterilir.

Anakütle Standart Sapması

Basit Serilerde

$$ \sigma = \sqrt{ { \Sigma (X_i - \mu)^2 } \over N } $$

Frekans Serilerinde

$$ \sigma = \sqrt{ { \Sigma f_i(X_i - \mu)^2 } \over N } $$

Gruplandırılmış Serilerde

$$ \sigma = \sqrt{ { \Sigma f_i(m_i - \mu)^2 } \over N } $$

Örneklem Standart Sapması

Basit Serilerde

$$ s = \sqrt{ { \Sigma (x_i - \bar x)^2 } \over n } $$

Frekans Serilerinde

$$ s = \sqrt{ { \Sigma f_i(x_i - \bar x)^2 } \over n } $$

Gruplandırılmış Serilerde

$$ s = \sqrt{ { \Sigma f_i(m_i - \bar x)^2 } \over n } $$

m: Sınıf Orta Sayısı, f: Frekans, σ: Anakütle Standart Sapması, s: Örneklem Standart Sapması

Formüller biraz daha detaylı yazılırsa…

Anakütle Standart Sapması

Basit Serilerde

$$ \sigma = \sqrt{ { \Sigma (X_i - { {\Sigma X_i } \over N })^2 } \over N } $$

Frekans Serilerinde

$$ \sigma = \sqrt{ { \Sigma (X_i - { {\Sigma X_i f_i } \over N })^2 } \over N } $$

Gruplandırılmış Serilerde

$$ \sigma = \sqrt{ { \Sigma (X_i - { {\Sigma m_i f_i } \over N })^2 } \over N } $$

Örneklem Standart Sapması

Basit Serilerde

$$ s = \sqrt{ { \Sigma (x_i - { {\Sigma x_i } \over n })^2 } \over n } $$

Frekans Serilerinde

$$ s = \sqrt{ { \Sigma (x_i - { {\Sigma x_i f_i } \over n })^2 } \over n } $$

Gruplandırılmış Serilerde

$$ s = \sqrt{ { \Sigma (x_i - { {\Sigma m_i f_i } \over n })^2 } \over n } $$

Normal dağılım grafikleri⁵ standart sapma ile hesaplanmaktadır. Ortalamanın 0 (sıfır) alınması durumunda “standart normal dağılım” olarak adlandırılmaktadır. Normal dağılımda 68-95-99.7 Kuralı adlı verilen özel bir kural geçerlidir. Bu kurala göre ortalamadan ±1σ (artı eksi 1 standart sapma) uzaklığa kadar olan alan, tüm olasılıkların %68.2’sini, ±2σ uzaklığa kadar olan alan %95.4’ünü, ±3σ uzaklığa kadar olan alan ise %99.6’sını kapsamaktadır. İlerleyen konularda normal dağılım detaylıca anlatılacak olup standart sapmanın tüm dağılım ölçüleri içerisinde neden en önemli ölçü olduğu dağılımı grafiklerinden de anlaşılabilir.

Varyans, standart sapmanın karesi olmakla birlikte anakütle için σ², örneklem içinse s² notasyonu ile gösterilir. Basit serilerde varyansı formülize etmek istersek

Anakütle için

$$ \sigma^2 = { { \Sigma(X_i - \mu)^2 } \over N } $$

Örneklem için

$$ s^2 = { { \Sigma(x_i - \bar x)^2 } \over n } $$

şeklinde gösterebiliriz. Örneklem hacminin 40’tan küçük olduğu serilerde n yerine (n-1) kullanılmalıdır.⁶

n ≤ 40 ise standart sapmanın formülü şu şekilde olmaktadır:

$$ s = \sqrt{ { \Sigma(x_i - \bar x)^2 } \over n - 1 } $$

Excel’de anakütle standart sapmasını hesaplamak için =STDSAPMA.P(), örneklem standart sapmasını hesaplamak içinse =STDSAPMA.S() formüllerini kullanabiliriz.

Uygulama: Bir sınıftan seçilen 10 öğrencinin sınav notları aşağıda verilmiştir.

$$ x = 40, 55, 60, 60, 65, 70, 75, 80, 85, 90 $$

Notların standart sapmasını bulunuz.

Standart sapmayı bulmak için öncelikle ortalamayı bulmalıyız.

$$ \bar x = {\Sigma x_i \over n} $$

$$ \bar x = {40 + 55 + 60 + 60 + 65 + 70 + 75 + 80 + 85 + 90 \over 10} = 68 $$

Standart sapmayı hesapladığımızda

$$ s = \sqrt{ { \Sigma(x_i - \bar x)^2 } \over n - 1 } $$

$$ s = \sqrt{ { (40-68)^2 + (55-68)^2 + ... + (85-68)^2 + (90-68)^2 } \over 10 - 1 } $$

$$ s = \sqrt{ 2090 \over 9 } = \sqrt{228.89} = 15.13 \approx 15 \text{ puan} $$

sonucunu elde ederiz. Dikkat ederseniz gözlem değerlerimiz 40’tan küçüktür. n ≤ 40 olduğu için payda kısmını n yerine n – 1 aldık.

Uygulama: Bir sınıftaki tüm öğrencilerin boy uzunlukları tabloda listelenmiştir.

Boy Uzunluğu	Öğrenci Sayısı
155 cm	1
160 cm	2
165 cm	7
170 cm	16
175 cm	18
180 cm	6
185 cm	4
190 cm	1
Toplam (Σ)	55

Boy uzunluklarının standart sapmasını bulunuz.

Öncelikle aritmetik ortalamayı buluruz.

Boy Uzunluğu (Xi)	Öğrenci Sayısı (fi)	Xifi
155 cm	1	155
160 cm	2	320
165 cm	7	1155
170 cm	16	2720
175 cm	18	3150
180 cm	6	1080
185 cm	4	740
190 cm	1	190
Toplam (Σ)	55	9510

$$ \mu = {\Sigma X_i f_i \over N} $$

$$ \mu = {155 + 320 + 1155 + 2720 + 3150 + 180 + 740 + 190 \over 55} = 172.91 \approx 173 \text{ cm} $$

Ardından standart sapmayı hesaplarız.

Boy Uzunluğu (Xi)	Öğrenci Sayısı (fi)	fi(Xi-µ)2
155 cm	1	1(155-173)2
160 cm	2	2(160-173)2
165 cm	7	7(165-173)2
170 cm	16	16(170-173)2
175 cm	18	18(175-173)2
180 cm	6	6(180-173)2
185 cm	4	4(185-173)2
190 cm	1	1(190-173)2
Toplam (Σ)	55	2485

$$ \sigma = \sqrt{ { \Sigma f_i(X_i - \mu)^2 } \over N } = \sqrt{2485 \over 55} = \sqrt{45.15} = 6.72 \approx 7 \text{ cm} $$

Uygulama: Bir sınıftaki tüm öğrencilerin boy uzunlukları tabloda listelenmiştir.

Boy Uzunluğu	Öğrenci Sayısı
150 – 159 cm	4
160 – 169 cm	12
170 – 179 cm	36
180 – 189 cm	8
190 – 200 cm	2
Toplam (Σ)	62

Boy uzunluklarının standart sapmasını bulunuz.

Öncelikle ortalamayı buluruz.

Boy Uzunluğu	mi	Öğrenci Sayısı (fi)	mifi
150 – 159 cm	155 cm	4	620
160 – 169 cm	165 cm	12	1980
170 – 179 cm	175 cm	36	6300
180 – 189 cm	185 cm	8	1480
190 – 200 cm	195 cm	2	390
Toplam (Σ)		62	10770

m_i sınıf orta sayısını belirtmektedir. (150 + 160) / 2 = 155 cm

$$ \mu = {\Sigma m_i f_i \over N} $$

$$ \mu = {(155 \times 4) + (165 \times 2) + (175 \times 36) + (185 \times 8) + (195 \times 2) \over 62} = 173.71 \approx 174 cm $$

Ardından standart sapmayı hesaplarız.

Boy Uzunluğu	mi	Öğrenci Sayısı (fi)	fi(mi-µ)2
150 – 159 cm	155 cm	4	4(155 – 174)2
160 – 169 cm	165 cm	12	12(165 – 174)2
170 – 179 cm	175	36	36(175 – 174)2
180 – 189 cm	185 cm	8	8(185 – 174)2
190 – 200 cm	195 cm	2	2(195 – 174)2
Toplam (Σ)		62	4302

$$ \sigma = \sqrt{ { \Sigma f_i(m_i - \mu)^2 } \over N } = \sqrt{4302 \over 62} = \sqrt{69.39} = 8.33 \approx 8 \text{ cm} $$

---

İstatistik konuları ve daha fazlası yeni sitemize taşınmıştır.

Veri Bilimi ve Veri Analizi | İstatistik için tıklayınız.

Sheppard Düzeltmesi

Düzeltilmiş Standart Sapma ya da Sheppard Düzeltmesi (Sheppard’s Correction) sınıflandırılmış (gruplandırılmış) serilerde standart sapmanın hatalı hesaplanması sonucu William Fleetwood Sheppard⁷ tarafından geliştirilen standart sapmadır.

$$ \sigma^* = \sqrt{ \sigma^2 - { c^2 \over 12} } $$

σ^*: Sheppard Düzeltmesi (Düzeltilmiş Standart Sapma), c: Sınıf Aralığı

Uygulama: Bir önceki örneğimizde standart sapmayı 8.3299 (8.33) bulmuştuk. Sınıf aralığı (c) 10’dur.

Düzeltilmiş standart sapmayı aşağıdaki gibi hesaplarız.

$$ \sigma^* = \sqrt{ \sigma^2 - { c^2 \over 12} } = \sqrt{ 8.3299^2 - { 10^2 \over 12} } = \sqrt{ 69.3871 - { 100 \over 12} } $$

$$ = \sqrt{69.3871 - 8.33} = \sqrt{61.0538} = 7.81 \approx 8 \text{ cm} $$

Sheppard düzeltmesi yapılabilmesi için serinin normal ya da normale yakın dağılması, frekansların büyük ve serinin iki ucunun da asimptotik sıfıra yaklaşması gerekmektedir.

---

Standart Hata (SE)

Standart sapmadan farklı olarak Standart Hata (Standart Error, SE)⁸ aynı anakütleden seçilen örneklemlerin standart sapmalarını karşılaştıran ölçü birimidir. Standart hata ne kadar küçükse anakütleye ait tahmin değerlerinin o kadar isabetli olduğu söylenebilir.

Anakütle için Standart Hata

$$ SE = { \sigma \over \sqrt N } $$

Örneklem için Standart Hata

$$ SE = { s \over \sqrt n } $$

Uygulama: 4000 birimlik anakütlenin standart sapması 8.42, bu anakütleden seçilen 40 birimlik örneklemin standart sapması ise 6.43’tür. Anakütle ve örneklem standart hatalarını karşılaştırınız.

Anakütle için Standart Hata

$$ SE = { \sigma \over \sqrt N } = { 8.42 \over \sqrt {4000} } = 0.1331 $$

Örneklem için Standart Hata

$$ SE = { s \over \sqrt n } = { 6.43 \over \sqrt {40} } = 1.0167 $$

Örneklem standart hatası (1.02), anakütle standart hatasından (0.13) çok büyük olduğu için seçilen örneklem uygun bir örneklem değildir.

---

Değişim Katsayısı (CV)

Değişim Katsayısı ya da Varyasyon Katsayısı (Coefficient of Variation, CV) bir serinin standart sapmasının aritmetik ortalamasına bölünüp 100 ile çarpılmasıyla elde edilir.

Anakütle için Değişim Katsayısı

$$ CV = { \sigma \over \mu } * 100 $$

Örneklem için Değişim Katsayısı

$$ CV = { s \over \bar x } * 100 $$

Uygulama: Aşağıda iki farklı semtin kira fiyatları listelenmiştir. Hangi semtin kira fiyatları daha ucuzdur?

A Semti	B Semti
4000	2600
4000	2800
4200	3000
4400	3200
4400	3200
4500	3400
4500	3500
4500	3500
4800	3600
5000	24000

İki semtin kira fiyatı ortalamaları ve standart sapmaları aşağıdaki gibidir:

A Semti Ort=4430 | s=316.40

B Semti Ort=5280 | s=6585.47

Verilere baktığımızda A semtinde kiraların B semtine göre daha yüksek olduğu görülmesine rağmen ortalamalar yanıltıcıdır. Bunun sebebi B semtinde 24000 TL gibi aykırı değere sahip bir kiranın olmasıdır. Bu sebeple değişim katsayılarını kullanmalıyız.

$$ CV_A = { s \over \bar x } * 100 = { 316.40 \over 4430 } * 100 = 7.14 $$

$$ CV_B = { s \over \bar x } * 100 = { 6585.47 \over 5280 } * 100 = 124.72 $$

A semtinin değişim katsayısı (7.14), B semtine göre (124.72) daha düşük olduğu için A semtinde kira fiyatları daha homojen dağılmıştır sonucuna varılabilir. B semtindeki aykırı değer, seriden çıkarıldığında B semtinin varyasyon katsayısı

$$ CV_B^* = { s \over \bar x } * 100 = { 342.78 \over 3200 } * 100 = 10.71 $$

hesaplanacaktır. Bu şekilde B semtinde ortalama kiraların (3200) A semtine göre (4430) daha ucuz olduğu sonucuna varılabilir.

---

SPSS'te Dağılım Ölçüleri

Değişim Aralığı, Standart Sapma, Varyans ve Standart Hata

İstatistik konuları ve daha fazlası yeni sitemize taşınmıştır.

Veri Bilimi ve Veri Analizi | İstatistik için tıklayınız.

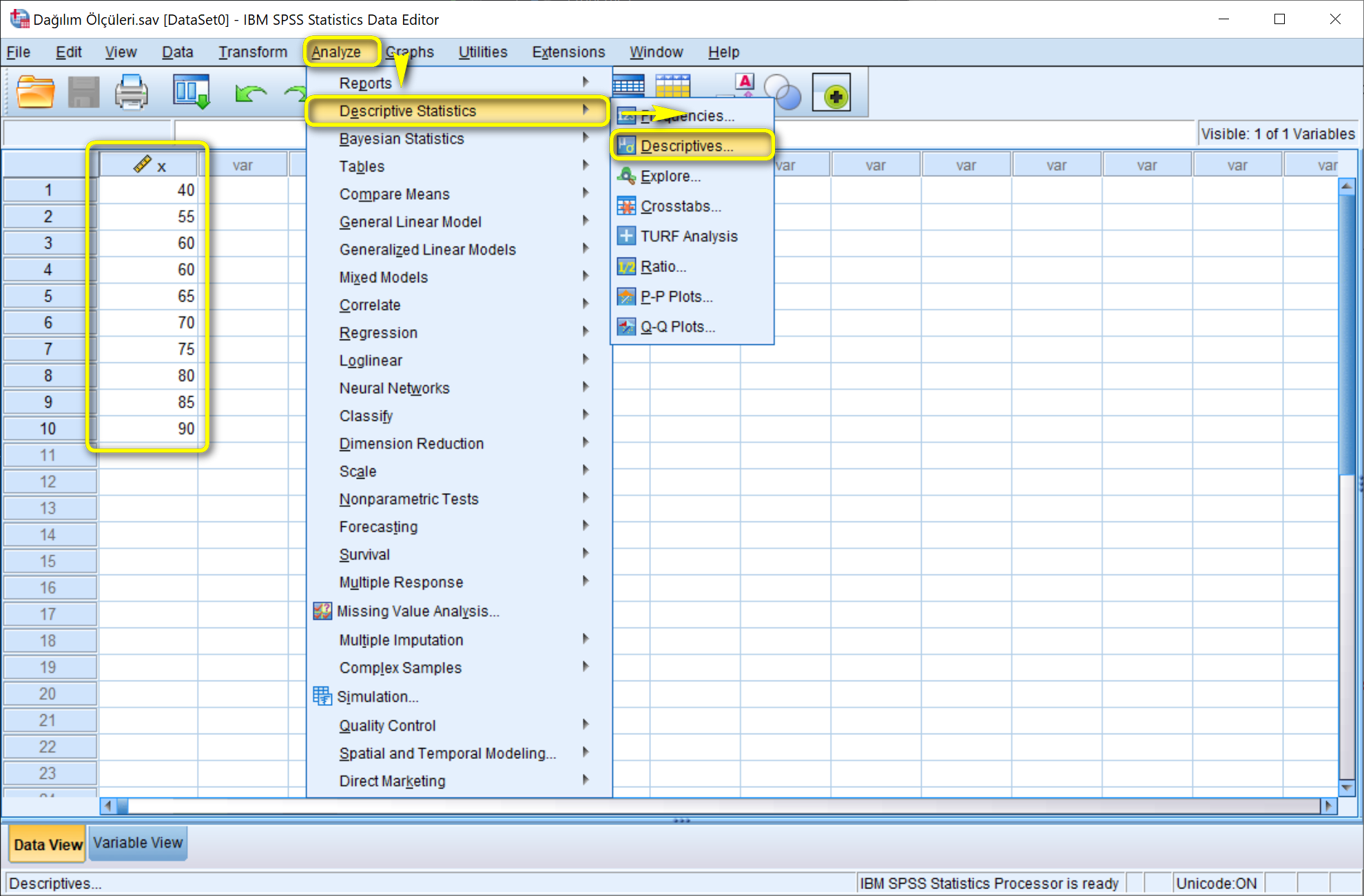
SPSS'te çok hızlı bir şekilde değişim aralığı, standart sapma, varyans ve standart hata değerleri hesaplanabilir.

Analyze > Descrpitive Statistics > Descriptives... yolu izlenir.

Descriptives penceresinde ilgili değişken Variable(s) alanına aktarılır ve ardından Options...'a tıklanır.

Açılan Descrpitives: Options penceresinde ilgili dağılım ölçüleri seçilir ve Continue'ya tıklanıldıktan sonra Descriptives penceresinde OK'a tıklanır.

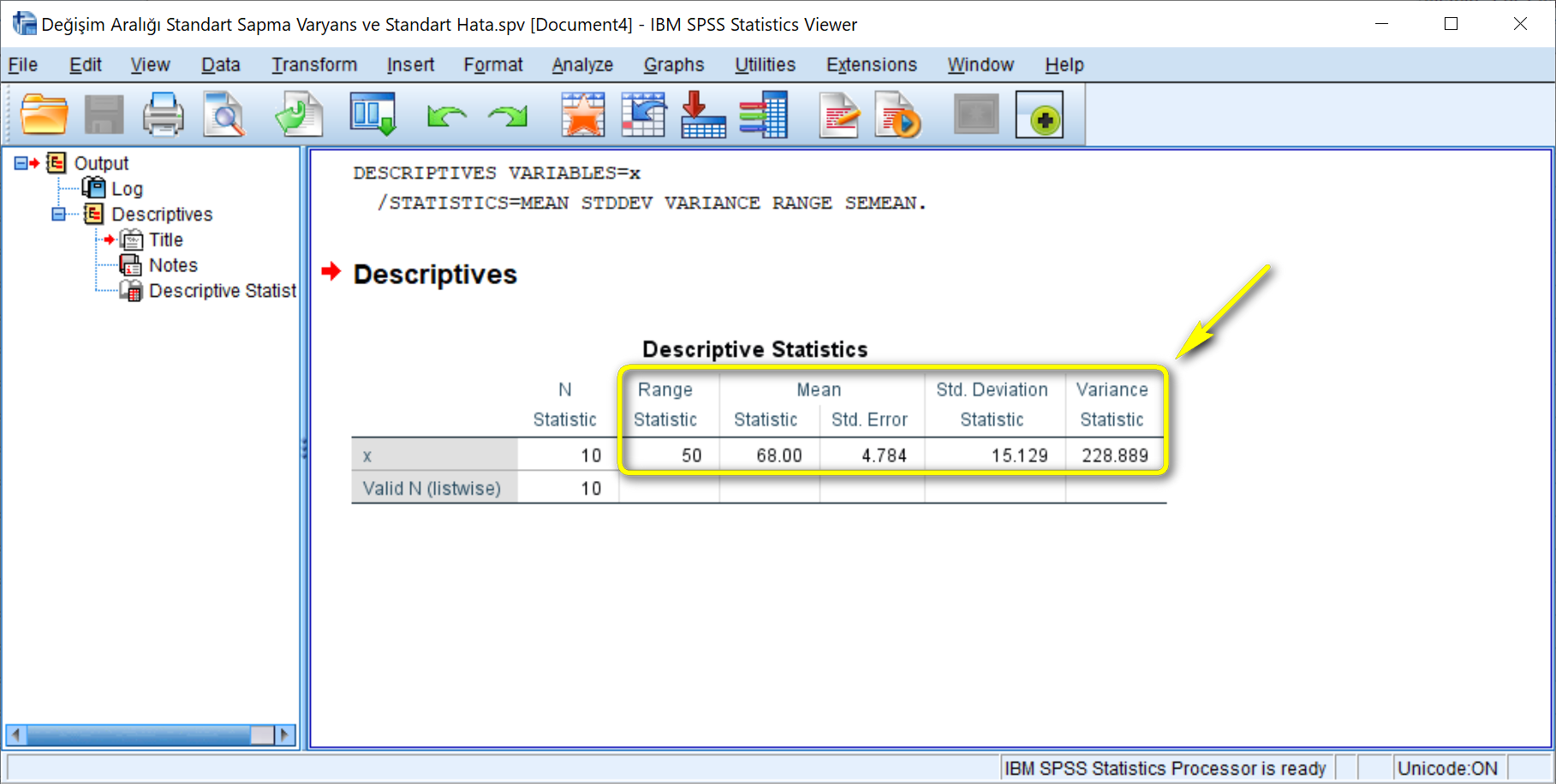
Sonuçlar Output (Çıktı) penceresinde görseldeki gibi listelenecektir.

Değişim Aralığı, Standart Sapma, Varyans ve Kartiller Arası Fark

SPSS'te değişim aralığı, standart sapma, varyans ve kartilleri arası farkı hesaplamak için aşağıdaki adımlar uygulanır.

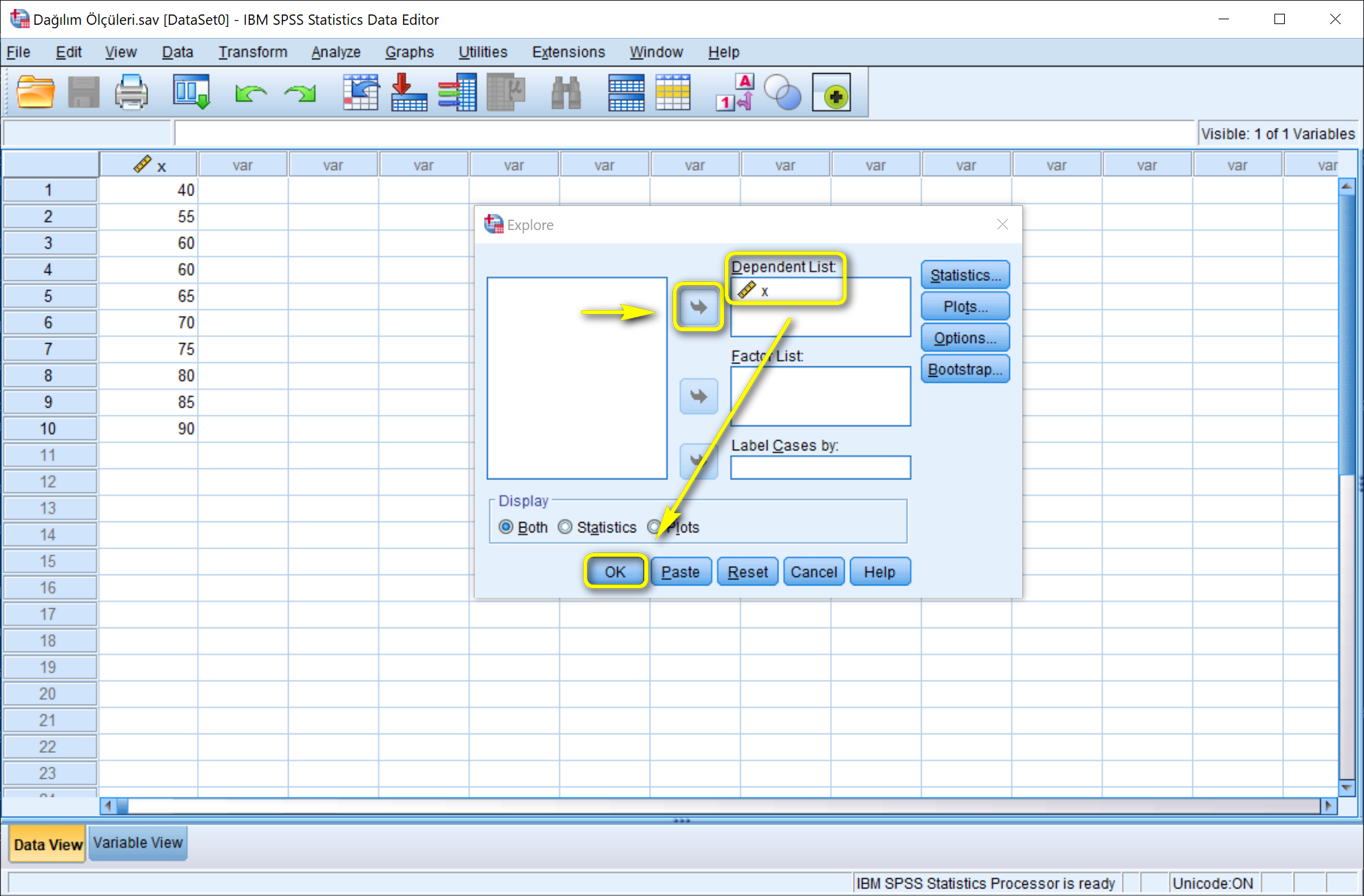
Analyze > Descrpitive Statistics > Explore... yolu izlenir.

Açılan Explore penceresinde x değişkeni Dependent List alanına aktarılır ve herhangi bir değişiklik yapılmadan OK'a tıklanır.

Output penceresinde ilgili dağılım ölçüleri görülebilir. Interquartile Range (IQR) kartiller arası farkı belirtmektedir.

---

Kutu Diyagramı (Box-Plot)

Kutu Diyagramı (Box Plot yada Boxplot) seri karşılaştırmalarında en sık kullanılan istatistik göstergelerinden biridir.

Öncelikle Q₁, Q₂ (medyan) ve Q₃ kartilleri bulunur. IQR (Kartiller Arası Fark) Q₃ ve Q₁ kartillerinin farkı ile hesaplanır. Serinin minimum değeri Q₁ kartilinden 1.5 IQR'ın çıkarılmasıyla, maksimum değeri ise Q₃ kartiline 1.5 IQR eklenmesiyle bulunur. Minimum ve maksimum dışında kalan tüm değerler aykırı değer (outlier) olarak adlandırılır.

Uygulama: x = 2, 22, 24, 24, 26, 28, 28, 28, 30, 98, 122 serisinin kutu diyagramını çiziniz.

Kutu diyagramını çizebilmek için Q₁, Q₂ ve Q₃ değerlerini bulmamız yeterlidir.

n: 11’dir. Gözlem sayısı tek sayı olduğu için

$$ Q_1 = { x_{ { n+2 } \over 4 } } = { x_{ { 11+2 } \over 4 } } = x_{3.25} \approx x_3 = 24 $$

$$ Q_2 = \tilde x = x_{ {n+1} \over 2} = { x_{ {11+1} \over 2} } = x_6 = 28 $$

$$ Q_3 = { x_{ { 3n+2 } \over 4 } } = { x_{ { 3(11)+2 } \over 4 } } = x_{8.75} \approx x_9 = 30 $$

Q₁ ve Q₃ kartilleri bulunduktan sonra IQR (Kartiller Arası Fark) hesaplanır.

$$ IQR = Q_3 - Q_1 = 30 - 24 = 6 $$

Son olarak Min ve Max değerlerinin hesaplanması yeterlidir.

$$ Min = Q_1 - 1.5(IQR) = 24 - 1.5(6) = 24 - 9 = 15 $$

$$ Max = Q_3 + 1.5(IQR) = 30 - 1.5(6) = 30 + 9 = 39 $$

Bulunan değerler diyagramın üzerine yerleştirilirse kutu diyagramı (boxplot) oluşacaktır. Diyagramdan da görüleceği üzere 2, 98 ve 122 değerleri aykırı değerlerdir. Bu değerler aynı zamanda seride yaklaşık %99 oranda normal dağılan değerlerin dışında yer almaktadır. Bu yüzden aykırı değer olarak adlandırılır.

Kutu diyagramları çoğunlukla seri karşılaştırmalarında kullanılır. Serilerin birbirlerinden farkını ayırt etmek için kullanılabilecek en iyi veri görselleştirme uygulamalarından biridir. Diyagramlar yatay çizilebileceği gibi yukarıdaki örnekte olduğu gibi dikey de çizilebilmektedir.

---

SPSS'te Kutu Diyagramı

SPSS'te kutu diyagramı (boxplot) çizmek oldukça basittir.

Seri değerleri girildikten sonra menüden Graphs > Legacy Dialogs > Boxplot... yolu izlenir.

Simple seçilir. Tek bir serinin kutu diyagramı çizilmek isteniyorsa "Summaries of seperate variables" seçimi yapılır ve Define'a tıklanır.

Değişken Boxes Represent alanına aktarılır ve OK'a tıklanır.

Kutu diyagramı görseldeki gibi oluşturulacaktır.

---

Sıra Sizde

Uygulama: Bir sınıftan seçilen 8 öğrencinin sınav notları aşağıda verilmiştir.

$$ x = 55, 60, 70, 75, 80, 85, 85, 90 $$

Serinin Değişim Aralığı'nı (Range'ini) bulunuz.

Yanıt: Değişim aralığını bulmak için seriden maksimum ve minimum değerleri çıkarmak yeterlidir.

$$ R = x_{max} - x_{min} $$

$$ R = 90 - 55 $$

$$ R = 35 $$

Değişim Aralığı (Range) 35 bulunur.

Uygulama: Aşağıda 9 birimden oluşan seri verilmiştir.

$$ x = 24, 26, 26, 28, 30, 32, 36, 38, 40 $$

Serinin Kartiller Arası Fark'ını (IQR'ını) bulunuz.

Yanıt: Kartiller Arası Farkı bulabilmek için Q₁ ve Q₃ kartillerini bulmamız yeterlidir.

$$ Q_1 = { x_{ { n+2 } \over 4 } } = { x_{ { 9+2 } \over 4 } } = x_{2.75} \approx x_3 = 26 $$

$$ Q_3 = { x_{ { 3n+2 } \over 4 } } = { x_{ { 3(9)+2 } \over 4 } } = x_{7.25} \approx x_8 = 38 $$

Q₃ ve Q₁ arasındaki fark Kartiller Arası Fark'ı verecektir.

$$ IQR = Q_3 - Q_1 = 38 - 26 = 12 $$

Kartiller Arası Fark 12 bulunur.

Uygulama: Aşağıda 5 değerden oluşan bir seri verilmiştir.

$$ x = 4, 8, 12, 16, 20 $$

Serinin standart sapmasını bulunuz.

Yanıt: Standart sapmayı bulmak için öncelikle ortalamayı bulmalıyız.

$$ \bar x = {\Sigma x_i \over n} $$

$$ \bar x = {4 + 8 + 12 + 16 + 20 \over 5} = 12 $$

Standart sapmayı hesapladığımızda

$$ s = \sqrt{ { \Sigma(x_i - \bar x)^2 } \over n - 1 } $$

$$ s = \sqrt{ { (4-12)^2 + (8-12)^2 + (12-12)^2 + (16-12)^2 + (20-12)^2 } \over 5 - 1 } $$

$$ s = \sqrt{ 160 \over 4 } = \sqrt{40} = 6.32 \approx 6 $$

6 olarak buluruz. Dikkat ederseniz gözlem değerlerimiz 40’tan küçüktür. n ≤ 40 olduğu için payda kısmını n yerine n – 1 aldık.

Uygulama: Aşağıda 5 değerden oluşan bir seri verilmiştir.

$$ x = 12, 12, 12, 12, 12 $$

Serinin standart sapmasını bulunuz.

Yanıt: Aslında bu soruda hesap yapmamıza bile gerek yok. Serideki tüm değerler birbirine eşitse serinin standart sapması daima 0 (sıfırdır).

Yine de bunu kanıtlamak istersek öncelikle ortalamayı bulmakla işe başlamalıyız.

$$ \bar x = {\Sigma x_i \over n} $$

$$ \bar x = {12 + 12 + 12 + 12 + 12 \over 5} = 12 $$

Standart sapmayı hesapladığımızda

$$ s = \sqrt{ { \Sigma(x_i - \bar x)^2 } \over n - 1 } $$

$$ s = \sqrt{ { (12-12)^2 + (12-12)^2 + (12-12)^2 + (12-12)^2 + (12-12)^2 } \over 5 - 1 } $$

$$ s = \sqrt{ 0 \over 4 } = \sqrt{0} = 0 $$

Görüleceği üzere standart sapma sıfırdır. Standart sapma değerlerin ortalamadan uzaklıklarının ölçüsüdür. Serideki hiçbir değer ortalamadan uzaklaşmamıştır. Bu sebeple standart sapma 0 bulunmuştur.

Uygulama: Aynı sayıda öğrenciden oluşan iki farklı sınıfın sınav puanlarına ait ortalama ve standart sapma değerleri aşağıda listelenmiştir.

$$ A Sınıfı: { \mu = 65, \sigma = 10 } $$

$$ B Sınıfı: { \mu = 70, \sigma = 25 } $$

Hangi sınıftaki notlar daha homojen dağılmıştır?

Yanıt: İki seri arasında homojenlik karşılaştırması yapılmak isteniyorsa daima Değişim Katsayısından (Varyasyon Katsayısından) faydalanırız.

$$ CV_A = { \sigma \over \mu } * 100 = { 10 \over 65 } * 100 \approx 15.38 $$

$$ CV_B = { \sigma \over \mu } * 100 = { 25 \over 70 } * 100 \approx 35.71 $$

A sınıfının Değişim Katsayısı (CV'si) sıfıra daha yakın olduğu için A sınıfındaki notlar B sınıfına göre daha homojen dağılmıştır diyebiliriz.

İstatistik konuları ve daha fazlası yeni sitemize taşınmıştır.

Veri Bilimi ve Veri Analizi | İstatistik için tıklayınız.

Navigasyon
<<< Önceki Konu	İçindekiler	Sonraki Konu >>>

Footnotes

1. Statistical Dispersion olarak da bilinir. ↩

2. Standart sapma kavramına birazdan değinilecektir. ↩

3. IQR için yabancı kaynaklarda midspread, middle 50%, H‑spread terimleri de kullanılmaktadır. ↩

4. Boxplot ↩

5. Normal distribution diagram ↩

6. Kimi kaynaklarda 30’dan küçük olması şartı aranmaktadır. ↩

7. 20 Kasım 1863 – 12 Ekim 1936 tarihleri arasında yaşayan Avustralyalı – İngiliz istatistikçi ↩

8. IBM SPSS Statistics’te standart sapma ile karışmaması için “Standart Error of The Mean” (SEM) terimi kullanılmaktadır. ↩