-
Notifications
You must be signed in to change notification settings - Fork 2
Sparse Matrix Storage Technology and Conjugate Gradient Method Report
- 稀疏矩阵存贮技术与共轭梯度法探究报告
-
格式定义:每一个非零元素用一个三元组表示,分别是(行号,列号,数值),以行号数组 Row[ ],列号数组 Column[ ],数值数组Data[ ]配合存储;
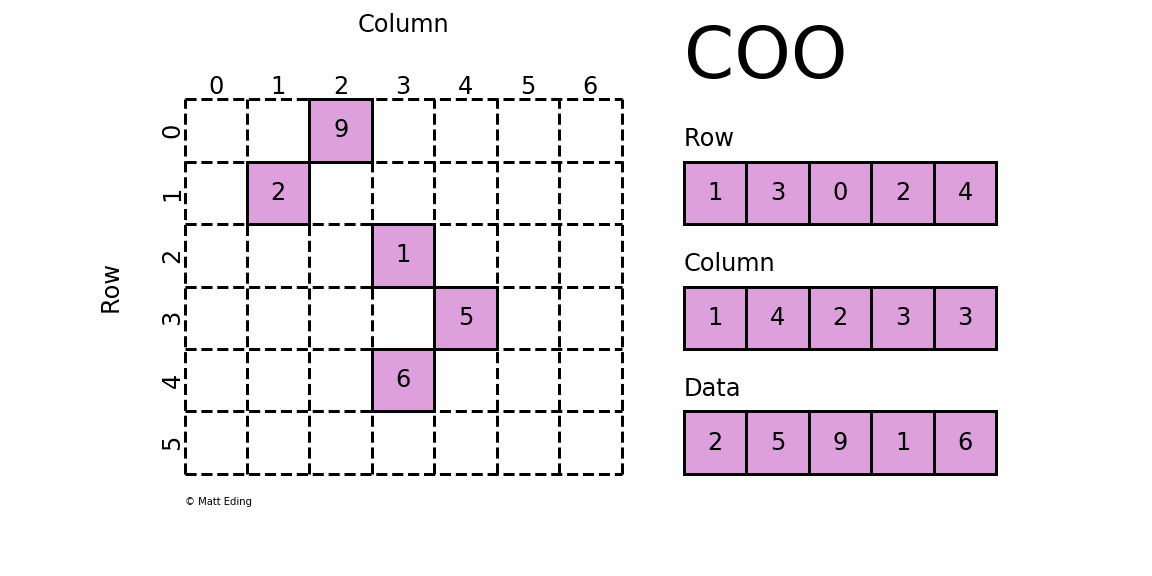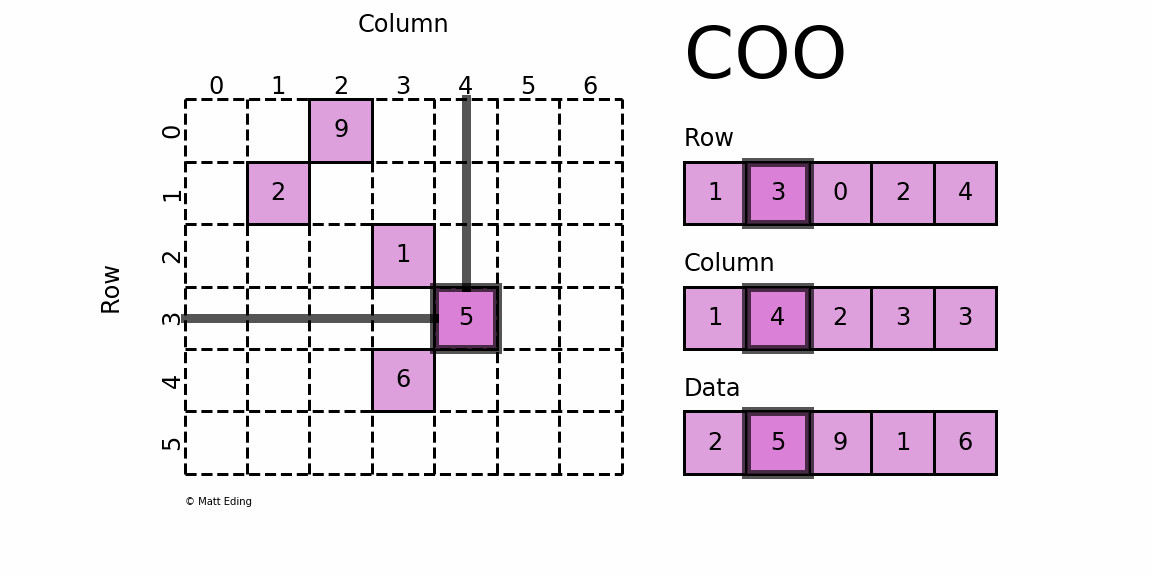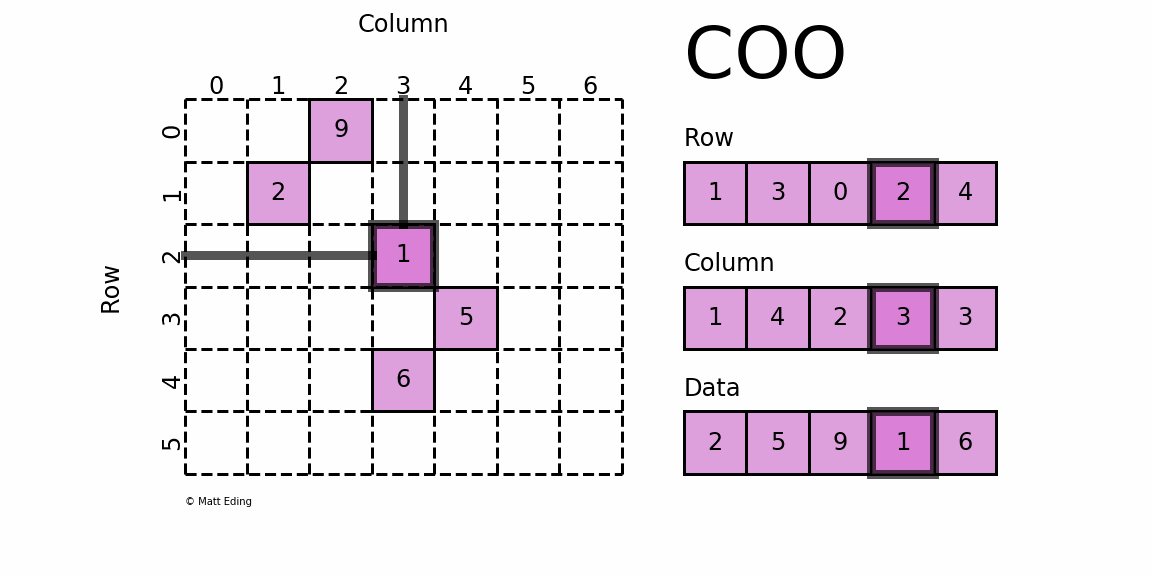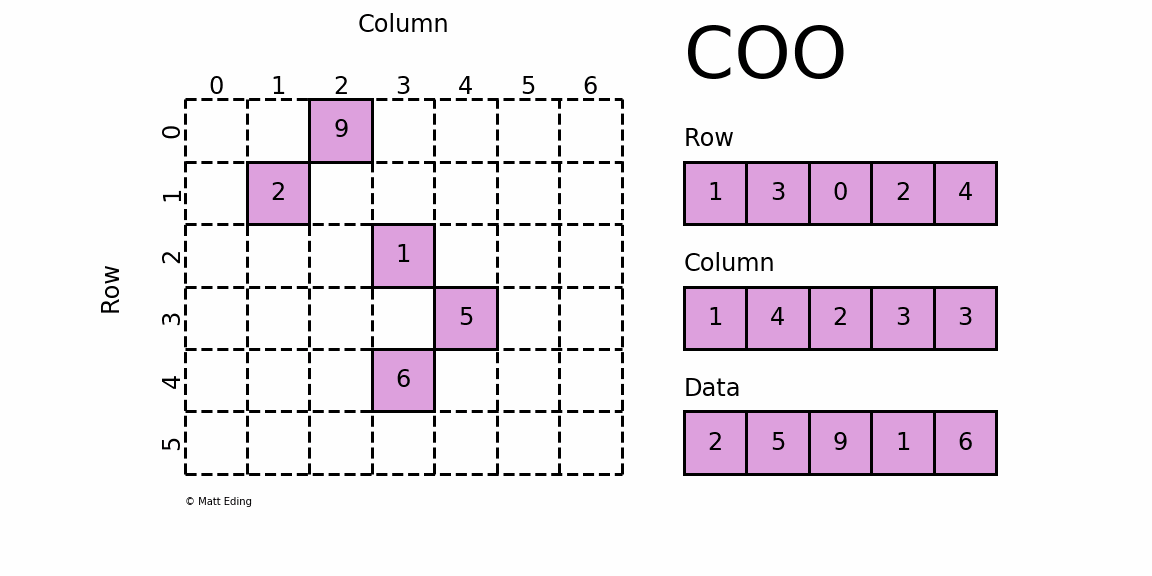
-
效率分析:
- 内存开销与非零元素数据量成正比;
- 随着数据量增加、稀疏程度提高,内存节省相当可观;
- 以 COO 格式管理数据,行指针与列指针被显示存储,管理数据的开销为固定成本,随着数据量增长,管理子阵列的开销小;
- 以 COO 格式存储数据,矩阵稀疏程度需要满足一定的条件才能节省内存,主要与元素类型和缩影数据类型有关:比如,一个存储32-bit的浮点类型数据的稀疏矩阵,索引使用32-bit的整型格式,那么只有当非零数据少于于矩阵的三分之一的时候才会节约存储空间。
-
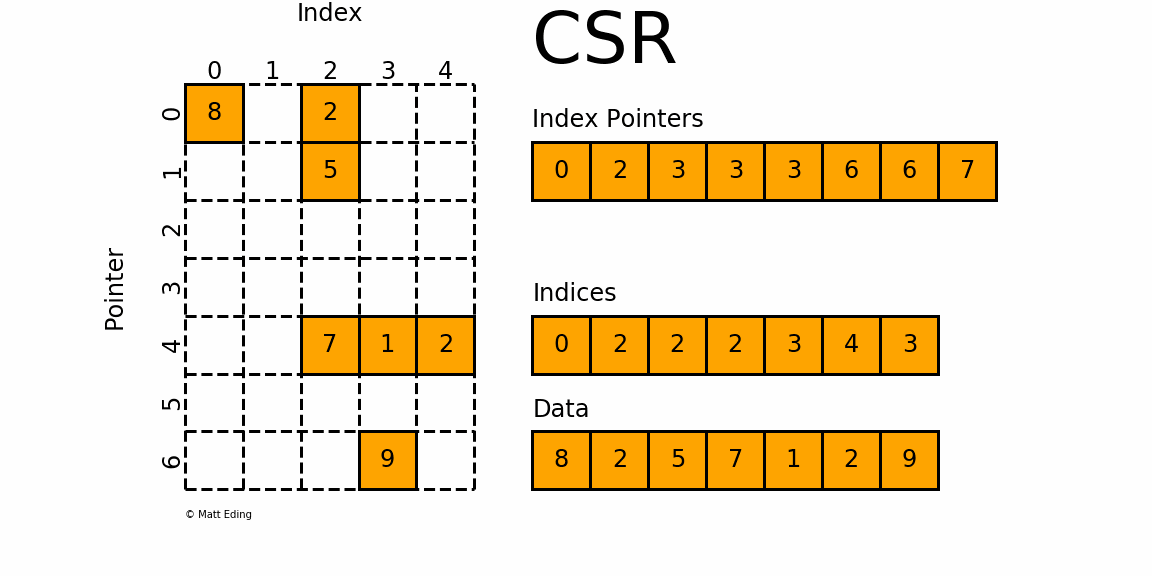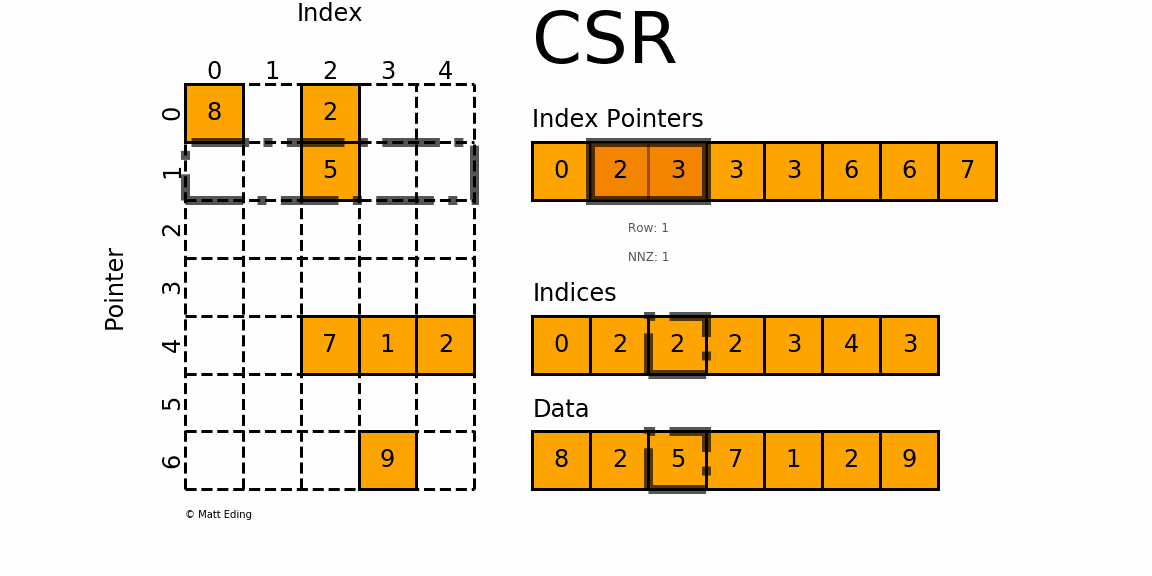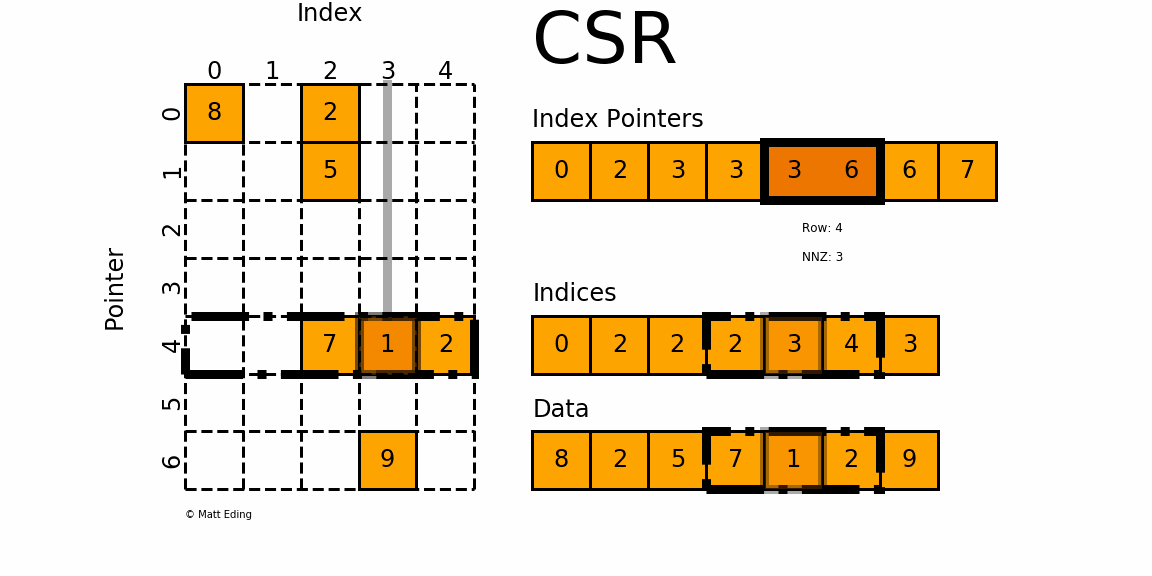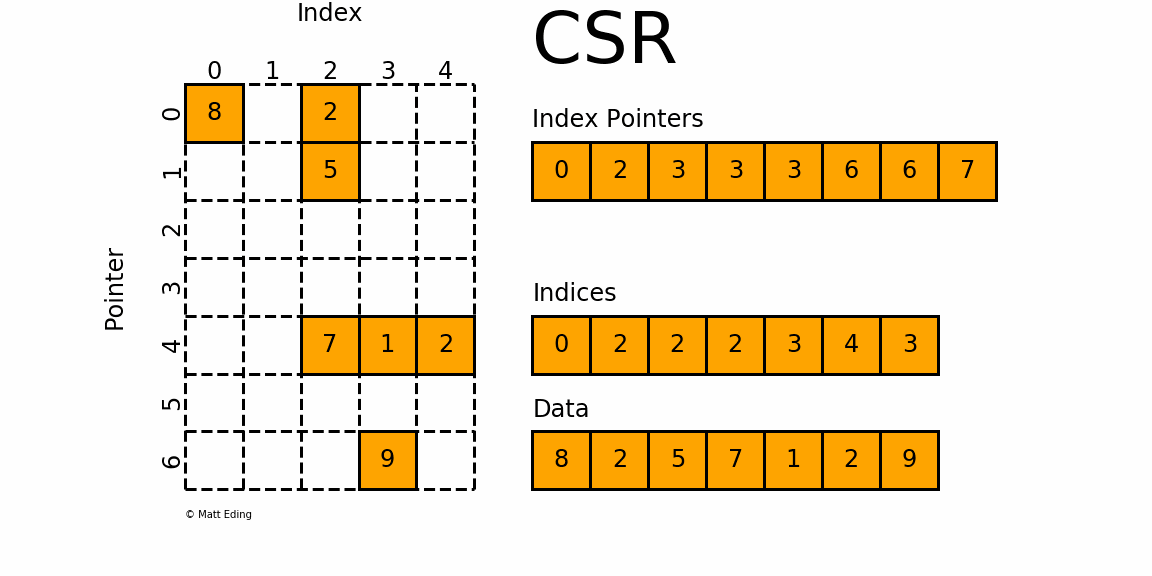
格式定义:非零元素以索引指针数组 Index_Pointers[ ]、索引数组 Indices[ ]、数值数组 Data[ ] 配合存储:
- 索引指针数组 Index_Pointers[ ] 存储每一行第一个非零元素的偏移量;
- 索引数组 Indices[ ] 标识非零元素对应的列值;
- 数值数组 Data[ ] 存储非零元素;
- 相邻两指针 Index_Pointers[n] 和 Index_Pointers[n+1] 表示当前元素位于矩阵的第 n 行,第 n 行的元素有 Data[Index_Pointers[n] : Index_Pointers[n+1]],对应的列号分别为 Indices[Index_Pointers[n] : Index_Pointers[n+1]];
-
效率分析:
- 内存开销与非零元素数据量成正比;
- 随着数据量增加、稀疏程度提高,内存节省相当可观;
- 以 CSR 格式存储数据,相较于 COO 格式进行了行压缩,改行号数组为偏移数组,存储数据量从非零数据数量减少到行数加一。
-
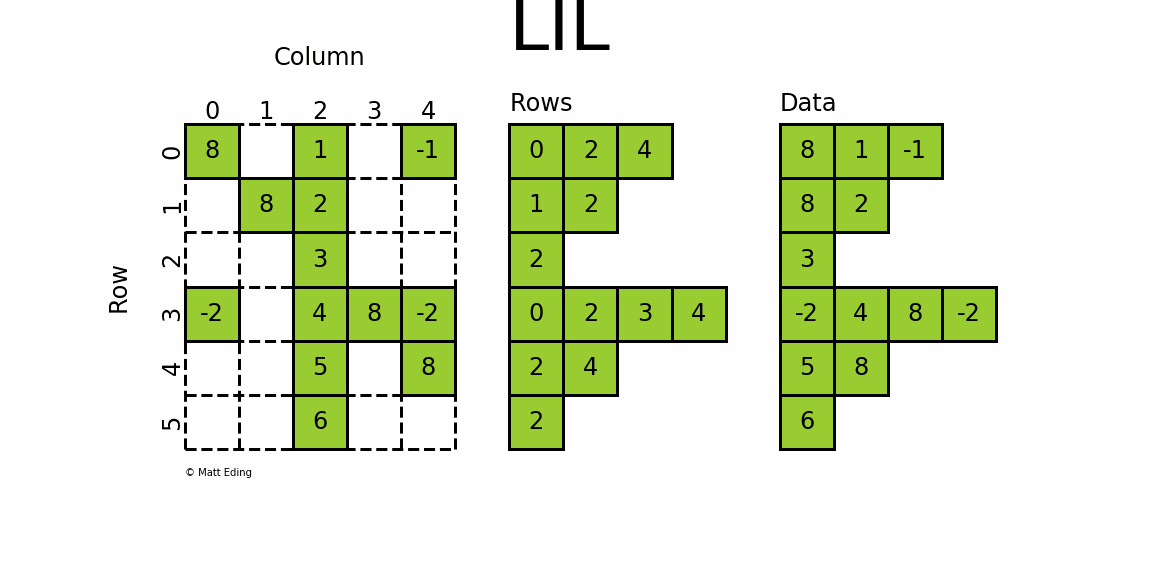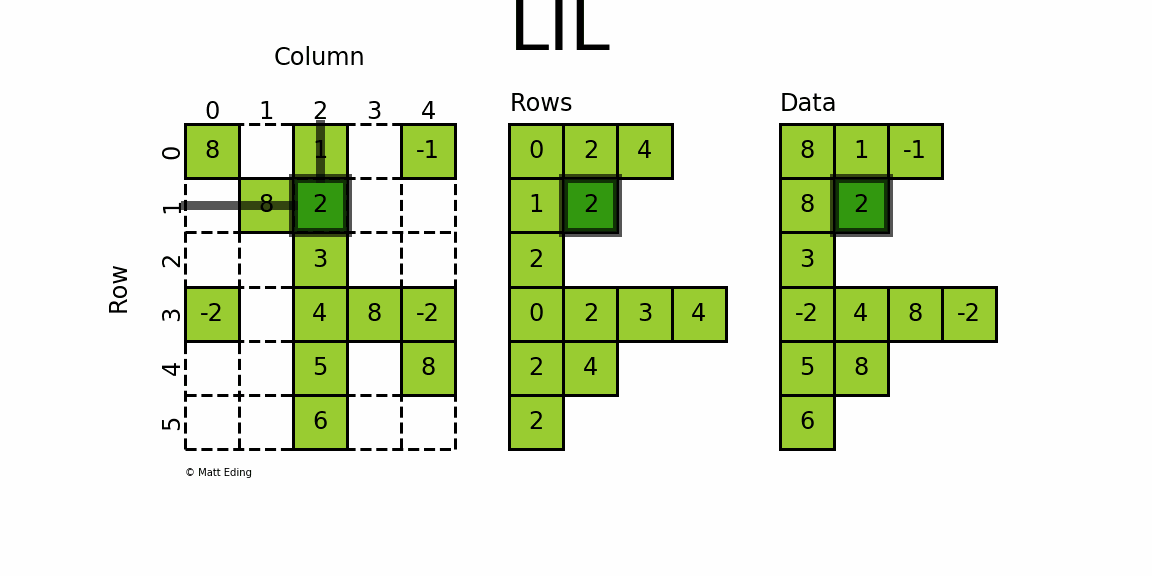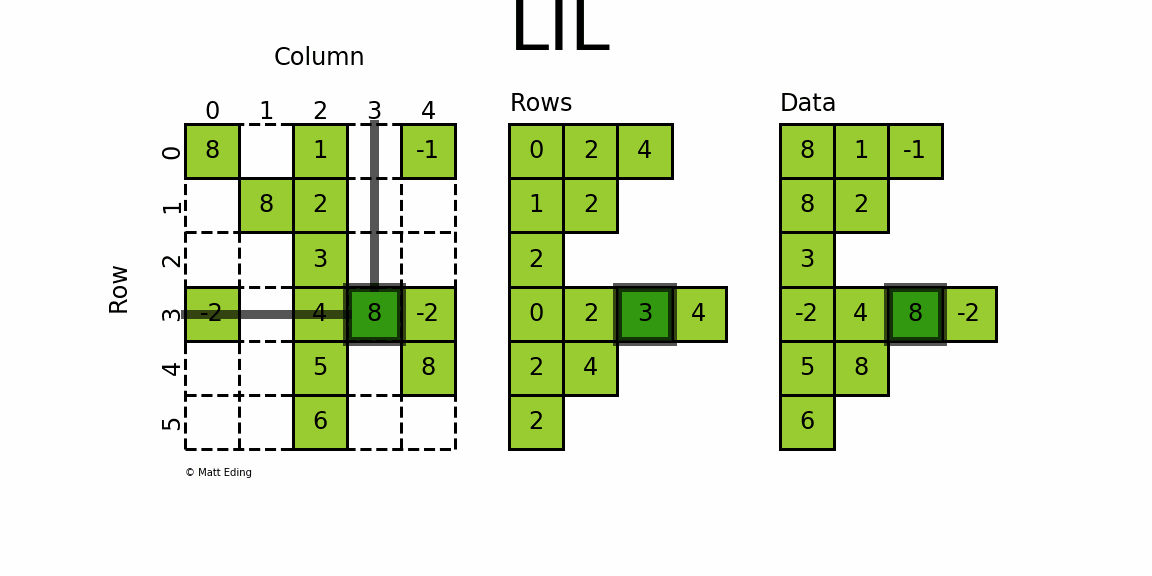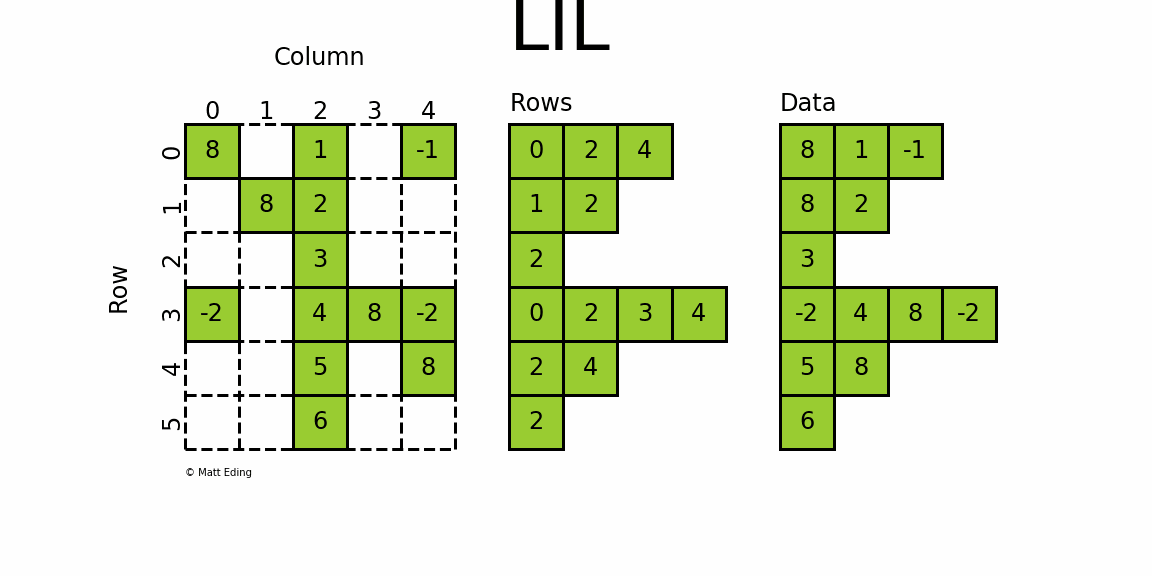
格式定义:将一个矩阵分为 Rows 和 Data 两个部分,按照 Rows 和 Data 对应位置进行一一存储,对应位置表示矩阵当中的一个元素
- Rows 的 每一行和原矩阵每一行对应,每一行元素个数等于矩阵该行个数。存储每个非零元的列号;
- Datas 的 形状和Rows一样。
-
效率分析:
- 内存开销与非零元素数据量成正比(两倍关系);
- 随着数据量增加、稀疏程度提高,内存节省相当可观;
- 由于Rows和Datas的形状一致,可以看出这个算法易于理解和实现。
-
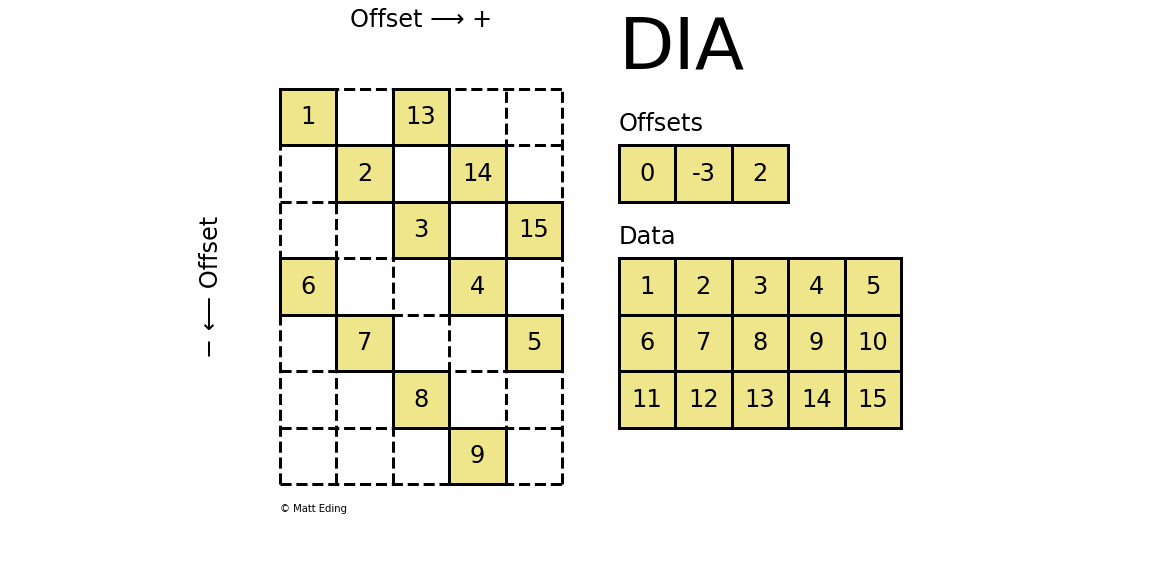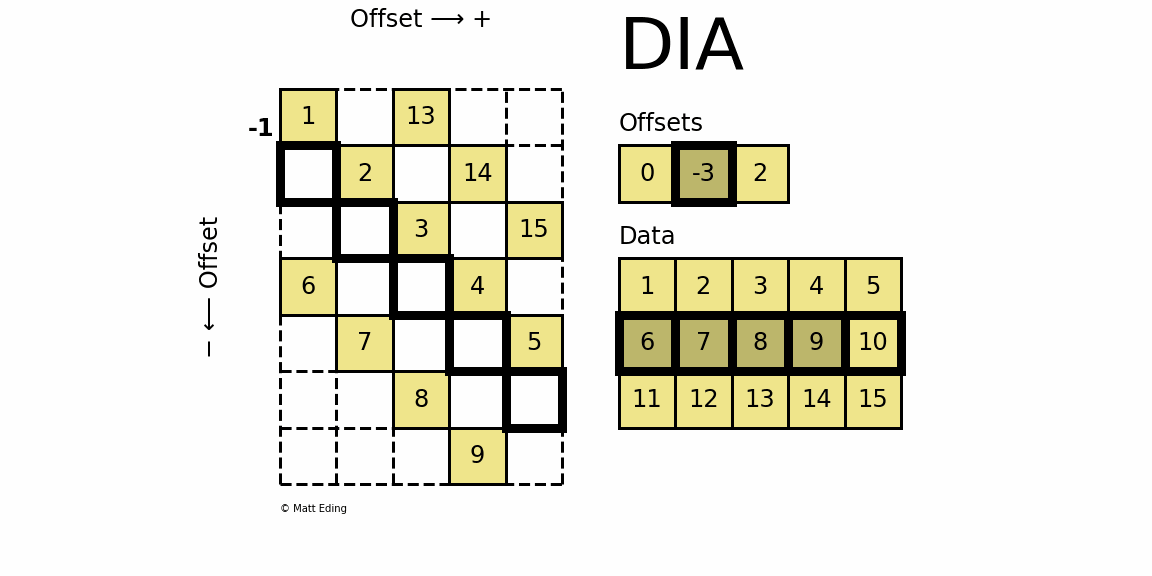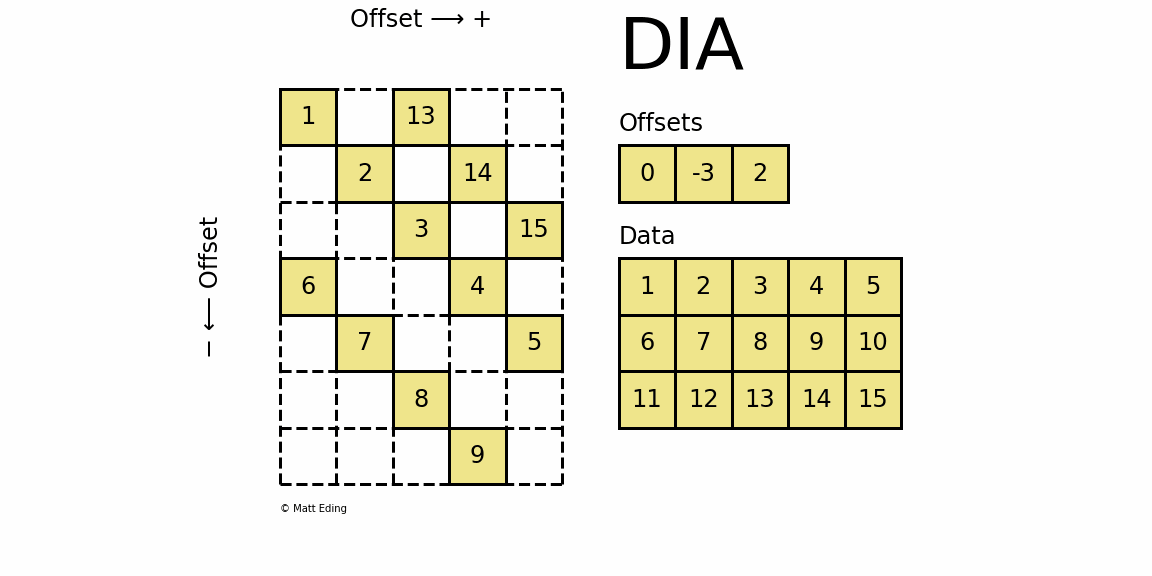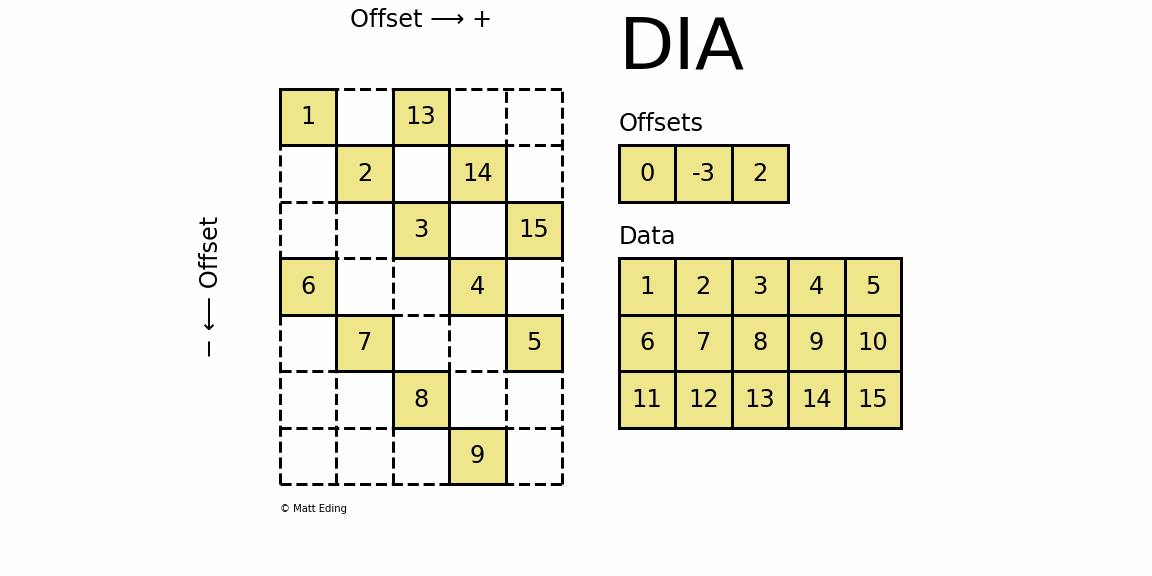
格式定义:将一个矩阵以对角线为Data的每一行为单位存储,Offset存储每一个对角行相对于起始对角行的偏移量,适合对角性强的稀疏矩阵。
- Offset用于定位对角行位置,每一位是每一个对角行相对于起始对角行的偏移。从左上的元素的对角行开始,其偏移量为0,在该对角行上方的对角行Offests值为正,反之为负。
- Data每一行与Offsets标识出的对角行对应,存储非零元。其中第一行每一个都是有效的,对于其余行中在原矩阵中未出现的对角行元素,用无效数(占位符标志)。
-
效率分析
- 所以如果原始矩阵就是一个对角性很好的矩阵那压缩率会非常高。
- 但是如果是随机的那效率会非常糟糕。Data的行数会非常多,可能出现Data的元素个数超过元素矩阵元素个数。
CUDA 为我们提供了较为高层的稀疏矩阵的库 cuSPARSE,它封装了三层 API,可以简便地支持密集矩阵和七种稀疏矩阵格式 (COO, CSR, CSC, ELL, HYB, BSR, BSRX) 的相互转换,同时提供了如 analysis(), solve()等运算接口。cuSOLVER 是基于 cuBLAS 和 cuSPARSE 库的一个对稀疏/稠密矩阵操作的库,包括矩阵分解和求解方程等内容,是个更高层的 API。结合 cuBLAS, cuSPARSE 和 cuSOLVER 三个稠密/稀疏矩阵的计算库可以写出高效的矩阵运算的程序。
虽然我们的代码实现尽量通过底层函数实现,但在一些诸如稀疏矩阵格式转化、矩阵压缩,分析稀疏矩阵元素依赖性等方面可以使用这些封装好的 API。通过学习这些高层 API 的用法也能为我们自己实现这些算法提供一些思路。
(* 本部分的内容只涉及该库的一些核心内容,大多翻译自NVIDIA Toolkit Documentation: cuSPARSE)
cuSPARSE 库包含一组用于处理稀疏矩阵的基本线性代数子例程。 它是在 NVIDIA$^®$ CUDA™ 运行时(它是 CUDA Toolkit 的一部分)之上实现的,旨在通过 C 和 C++ 进行调用。 库例程可以分为四类:
- 级别1:稀疏格式的向量和密集格式的向量之间的操作;
- 级别2:稀疏格式的矩阵与密集格式的向量之间的运算;
- 级别3:在稀疏格式的矩阵和一组密集格式的向量之间进行运算(通常也可以将其视为高密集矩阵);
- 转换:允许在不同矩阵格式之间进行转换以及对 CSR 矩阵进行压缩的操作。
下图展示了不同 Level 下 cuSPARSE 的一些函数调用。
如上面的介绍所说,cuSPARSE 支持七种稀疏矩阵格式,大多都在上一节中介绍过了,这里就来探究一下这些类型都是如何在 cuSPARSE 库中具体存储的。这里只介绍其中三种。
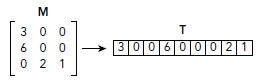 Fig 2-1. Dense Format Fig 2-1. Dense Format
|
 Fig 2-2. Coordinate (COO) Fig 2-2. Coordinate (COO)
|
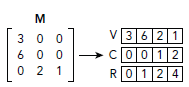 Fig 2-3. Compressed Sparse Row (CSR) Fig 2-3. Compressed Sparse Row (CSR)
|
假设密集矩阵
| 变量 | 类型 | 描述 |
|---|---|---|
m |
(integer) | 矩阵的行数。 |
n |
(integer) | 矩阵的列数。 |
ldX |
(integer) |
|
X |
(pointer) | 指向包含矩阵元素的数据数组。 假定为 |
例如,具有前导维 ldX 的
| 变量 | 类型 | 说明 |
|---|---|---|
nnz |
(integer) | 矩阵中非零元素的个数。 |
cooValA |
(pointer) | 指向长度为 nnz 的数据数组,该数据数组以行为主格式保存 |
cooRowIndA |
(pointer) | 指向长度为 nnz 的整数数组,该整数数组包含数组 cooValA 中相应元素的行索引 |
cooColIndA |
(pointer) | 指向长度为 nnz 的整数数组,该整数数组包含数组 cooValA 中相应元素的列索引 |
例如,考虑下面的

CSR 与 COO 格式的唯一不同之处在于,包含行索引的数组被压缩为 CSR 格式。$m \times n$ 稀疏矩阵
| 变量 | 类型 | 描述 |
|---|---|---|
nnz |
(integer) | 矩阵中非零元素的个数。 |
csrValA |
(pointer) | 指向长度为 nnz 的数据数组,该数据数组以行为主格式保存 |
csrRowPtrA |
(pointer) | 指向长度为 |
csrColIndA |
(pointer) | 指向长度为 nnz 的整数数组,该整数数组包含数组 csrValA 中相应元素的列索引 |
再次考虑下面的

上述三种(包括稠密矩阵)数据格式各有各擅长的方面。下图列出了 cuSPARSE 支持的一些数据格式以及各自的最佳使用场景:
从前文可知,这个数据转换的过程应该尽量避免,转换不仅需要有计算的开销,还有额外存储的空间浪费。还有就是在使用 cuSPARSE 也应该尽量发挥其在稀疏矩阵存储上的优势。因为 cuSPARSE 的数据格式众多,其用来转换的API也不少,下图列出了这些转换API。左边那一列是要转换的目标格式,为空表示不支持两种数据格式的转换,尽管如此,用户还可以通过多次转换来实现未显示支持的转换 API,比如 dense2bsr 没有被支持,但是我们可以使用 dense2csr 和 csr2bsr 两个过程来达到目的。
(* 本部分的内容是 NVIDIA Toolkit Documentation: cuSOLVER 的与线性矩阵求解内容的概括)
cuSolver 库是一个基于 cuBLAS 和 cuSPARSE 库的高级包。它由两个对应于两套 API 的模块组成:
- 单 GPU 上的 cuSolver API
- 多 GPU 单节点的 cuSolverMG API
cuSolver 的目的是提供有用的类似于 LAPACK 的功能,例如用于稠密矩阵的通用矩阵分解和三角求解例程,稀疏最小二乘法求解器和特征值求解器。 此外,cuSolver 还提供了一个新的重构库,可用于求解具有共享稀疏模式的矩阵序列。
cuSolver 将三个独立的组件结合在一起,分别为 cuSolverDN, cuSolverSP 和 cuSolverRF。cuSolverDN 提供了一些列如求解线性系统、最小二乘法的稠密矩阵的算子接口;而 cuSolverSP 则是为稀疏矩阵提供上述算子的接口;最后一部分是 cuSolverRF,它是一种稀疏重构包,在求解只有系数变化但稀疏模式不变的矩阵序列时,它可以提供非常好的性能。
以下内容着重讨论 cuSolverSP API。
下表展示了 cuSolverSP 关于线性算子的 API:
| routine | data format | operation | output format | based on |
|---|---|---|---|---|
csrlsvlu |
csr |
linear solution (ls) | vector (v) | LU (lu) with partial pivoting |
csrlsvqr |
csr |
linear solution (ls) | vector (v) | QR factorization (qr) |
csrlsvchol |
csr |
linear solution (ls) | vector (v) | Cholesky factorization (chol) |
如上所述 cuSolver 库只提供了基于 LU、SVD 和 LU 等基于矩阵分解的线性方程组的求法,通过检索,我们发现早些时候的 GPU 加速实现的 LAPACK 数值线性代数库 CULA 提供了大型稀疏线性系统的共轭梯度解法的函数接口,如下图所示。只是该计算框架早已被弃用,取而代之的正是 cuSPARSE 和 cuSOLVER。
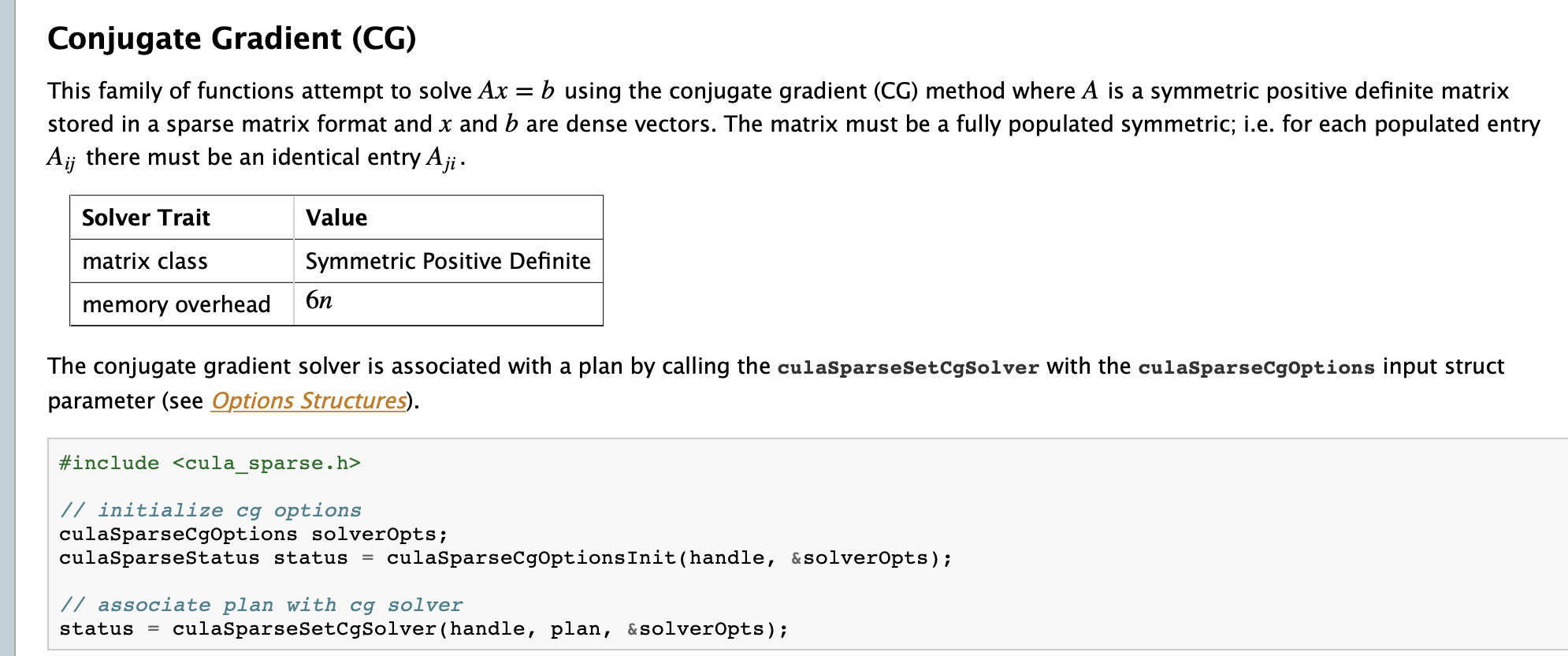
将稀疏的系数矩阵从文件中读取出,并用 cuSPARSE 库中的稀疏矩阵存储格式转换为 CSR 存储格式,然后在共轭梯度法的每步计算中涉及到稀疏的系数矩阵的部分使用 cuSPARSE 库中的函数(如:cusparseScsrmv)直接进行计算,不涉及稀疏矩阵的运算使用 cuBLAS 的函数(如 cublasSaxpy、cublasSdot )进行计算。
这部分代码的地址:https://github.com/1751200/Xlab-k8s-gpu/tree/master/ConjugateGradientSparse
即维护了一个统一的内存池,在 CPU 与 GPU 中共享。使用了单一指针进行托管内存,由系统来自动地进行内存迁移。由于共轭梯度法需要很多的中间变量(包括一些数组),所以可以直接使用统一寻址的方式为所需的变量和数组开辟内存,从而避免手动地内存迁移。
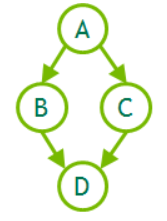
CUDA 图是 CUDA10 新推出的是异步任务图像 (Task-Graph) 编程模型,让内核启动和执行更高效。一个图由一系列操作组成,如内存拷贝和内核启动,这些操作通过依赖关系连接,并将执行与定义分开,图允许定义一次重复运行的执行流,这种图特别适合具有迭代结构的计算。所以在共轭梯度法中我们就能定义一个图,其中的每个节点定义为共轭梯度法迭代中的一个计算步骤,在定义完一轮迭代中所有的就算步骤后,就形成了一张计算图,接着在每轮迭代中会真正地去执行图中所有的节点。在这种情况下,图的定义与其执行分离了,能够降低CPU启动内核的成本,还使CUDA驱动程序能够执行许多优化,从而提高执行性能。
-
硬件环境
- CPU: Intel i7-7700HQ
- GPU: NVIDIA GeForce GTX 1050
-
软件环境
- Microsoft Visual Studio Community 2017 15.9.10
- Nvidia Cuda 10.1.120
-
运行环境
- Visual C++ 2017
我们使用 Matlab 生成了大小为
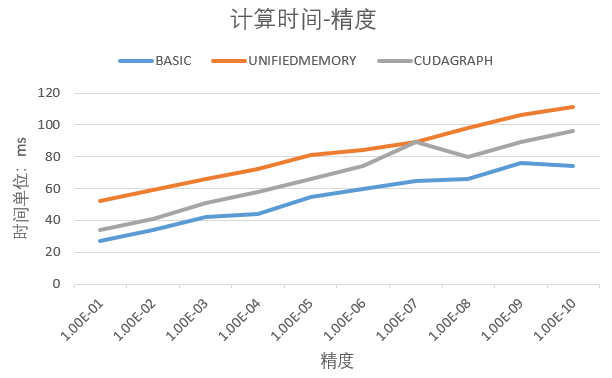
从图中可以看出基于稀疏存储的共轭梯度法的 GPU 版本即使在非零元的个数为百万级别的情况下,也只需很短的时间就能达到很高的精度。在实验中,没有经过任何优化的方法的运行速度反而是最快的,这是因为:
- 统一寻址虽然避免了手动的内存迁移,但其从内存池中的读取速度是没有直接从 GPU 内存中读取来得快,所以读取的消耗增加了
- 我们基于共轭梯度法构建的 CUDA 计算图,相对来说十分简单,总共就 5 个节点,而且迭代次数较少(最高迭代次数大概在 160 次左右),所以无法体现出计算图的性能优化。
我们在此之前实现了一个不使用稀疏矩阵存储方式的共轭梯度下降法(实现 CPU 和 GPU 版本),下图展示了对
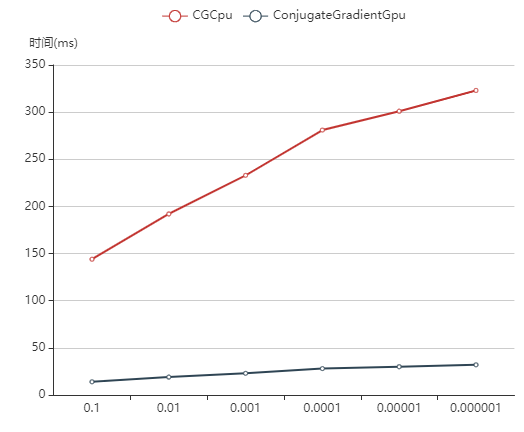
可以看到 GPU 上的共轭梯度算法对于约一百万元素的矩阵求解运算,收敛到
但实际上,以上结论是很不严谨的。原因在于稀疏矩阵的求解效率在很大程度上取决于矩阵的条件数:
$$
\text{cond}(A)=|A|\cdot|A^{-1}|
$$
条件数是判断矩阵病态与否的一种度量,条件数越大矩阵越病态。在线性方程组的求解问题中,条件数事实上表示了矩阵计算对于误差的敏感性。对于线性方程组
在我们的测试中,我们在使用 Matlab 函数 sprandsym 随机生成稀疏对称正定矩阵时,设定的条件数近似为
一般情况下,对于不是过于病态的稀疏矩阵,我们通过多次测试发现,程序在矩阵数据的读取上花费的时间远远超过了矩阵计算花费的时间。由于 Matlab 生成大型矩阵所花费的时间过长,我们没有测试更大的稀疏矩阵,而当前百万级别非零元的计算时间太短,参考的价值不大;因此关于矩阵大小、条件数对运算时间的影响有待进一步探究。

Software Engineering, Fall 2019 & Software Test, Spring 2020.
It is a collaborative and interdisciplinary project drawing on expertise from School of Software Engineering & College of Civil Engineering, Tongji University.




