A miscellaneous repository for anything having to do with computation in the context of Graph Theory
This section deals with the problem discussed my Matt Parker here, here and in his book "Things to Make and Do in the Fourth Dimension" with regards to his conjecture: That all consecutive integer sequences that exceed 25 can be rearranged such that the adjacent numbers sum to a square number, as well as 15, 16, 17, 23. One natural way to tackle this is using Hamiltonian paths on graphs like Parker did. A brute force search up to 299 was carried out by Charlie Turner and the code can be found here where the conjecture was found to hold.
This subsection is currently only serving as a "data collection" centre where various data about such graphs is collected for anyone who needs to do an analysis.
Due to the symbolic nature of the code and the size of the matrices undergoing the operations. I only managed to generate the characteristic polynomials C = det(A - xI) up to a degree of 34 and can be seen here. It is curious to note that quite a lot of adjacency matrices are singular (i.e. they are not invertible, det(A)=0, the polynomial has a y-intercept at 0). It is also interesting how rare odd-valued determinants are, even though the sample size is quite small.
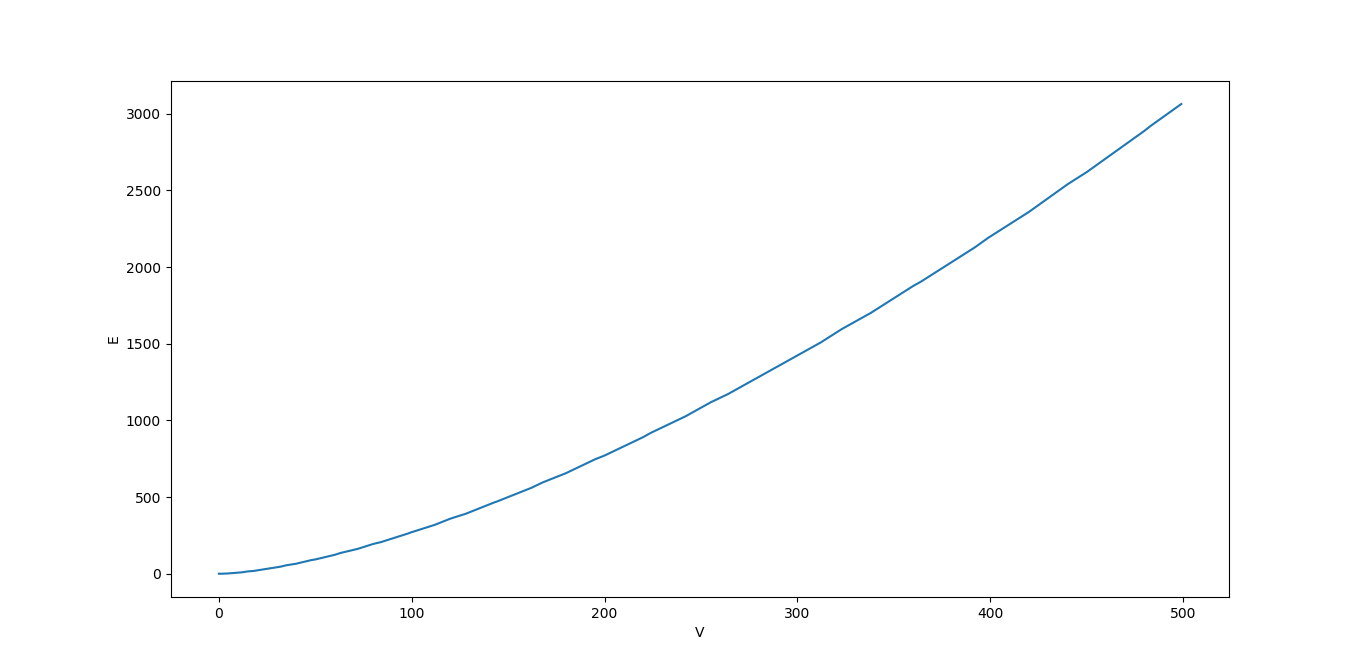
This was by far the easiest exhaustive lists to run. It basically counts the edges on each graph and finds the minimum, average and maximum degrees within the graph. Using the Handshake Lemma the script was made a bit more efficient by calculating the average degree directly from the number of edges as 2E/n. The list of the obtained values can be found here as well as a plot of the number of edges as a function of the number of edges.
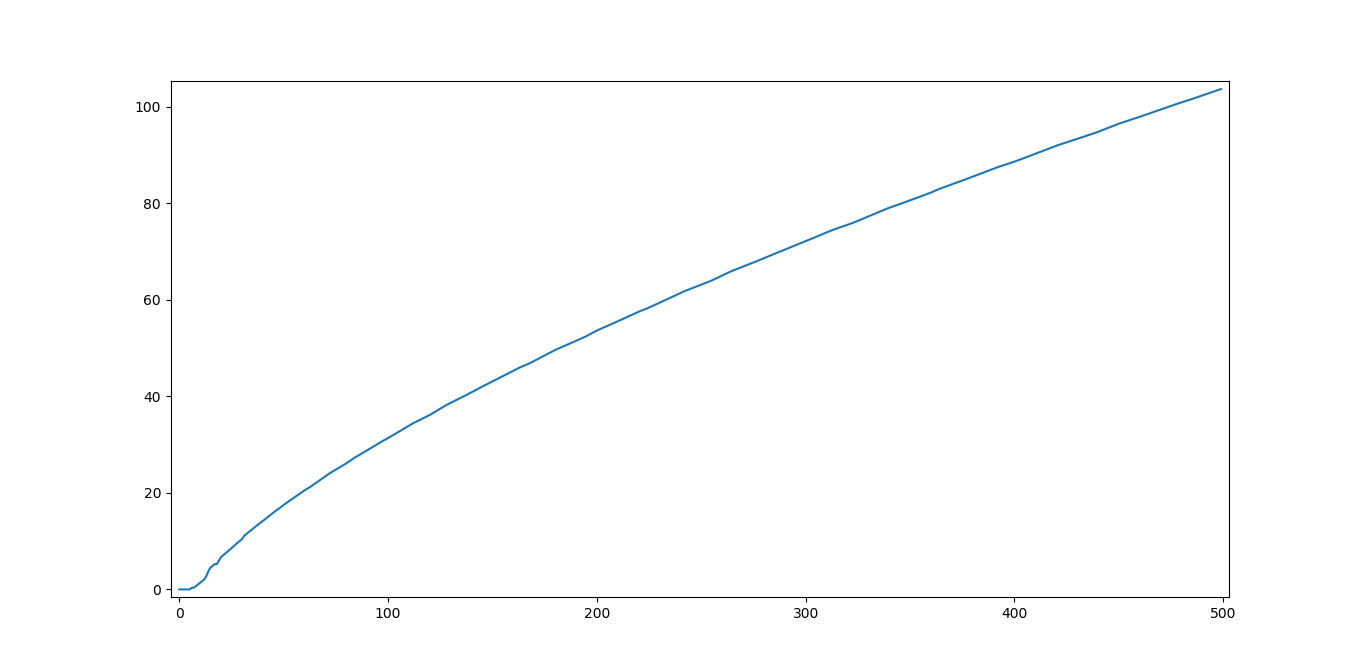
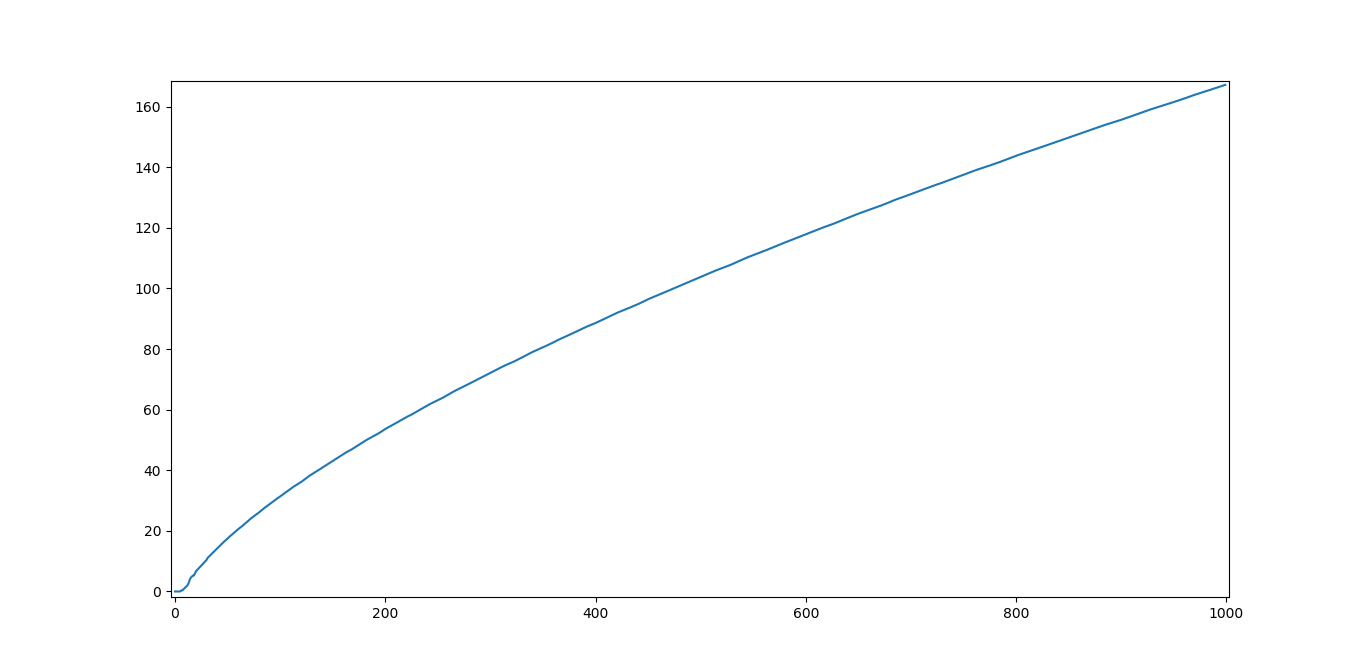
This result came out of a curiosity I had. Given that the Shannon Entropy is given by the sum of terms of the form -plog(p) or more simply as the expectation E[-log(p)], imagine being on a vertex v and choosing an edge randomly and uniformly (for whatever reason). the probability of choosing each node is p=1/deg(v). Now substituting this into the Shannon Entropy formula we would be summing terms of the form -plog(p) = log(deg(v))/deg(v). So I decided to investigate how this quantity changes with graph size. A .CSV file with the values can be found here and I plotted the values up to 500 and up to 1000 vertices.
