The Kraken Pathfinding

A multithreaded tentacle-based pathfinding library for holonomic and nonholonomic robotic vehicles

What is Kraken ?

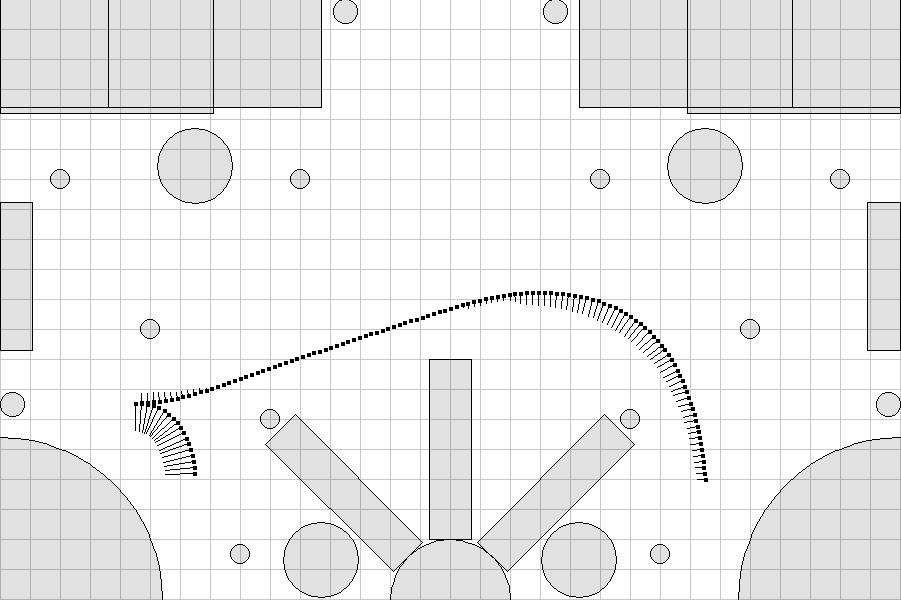
Kraken finds a trajectory followable by a car-like vehicle in the form of a list of points.

Features

The trajectory created by Kraken has several properties, making it suitable for robotic vehicles, namely:

• position continuity (G0 continuity), orientation continuity (G1 continuity) and curvature piecewise continuity (piecewise G2 continuity);
• handles forward and backward movement;
• takes into account the limited linear acceleration and deceleration;
• limits the radial acceleration.

Kraken has two default modes:

• find a path given a start position, a start orientation and an end position;
• find a path given a start position, a start orientation, an end position and an end orientation.

You can easily add new modes that suit your need.

Roadmap

A roadmap is available in the wiki of the project: https://github.com/PFGimenez/The-Kraken-Pathfinding/wiki/Roadmap

Why Java ?

For legacy reasons, mainly.

Getting Kraken

Precompiled .jar

You can download the latest stable and unstable versions of Kraken at https://github.com/orgs/kraken-robotics/packages.

Maven installation

If you want to use this library in one of your maven project, create a file ~/.m2/settings.xml that contains:

<settings xmlns="http://maven.apache.org/SETTINGS/1.0.0"
xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"
xsi:schemaLocation="http://maven.apache.org/SETTINGS/1.0.0
                    http://maven.apache.org/xsd/settings-1.0.0.xsd">

<activeProfiles>
    <activeProfile>github</activeProfile>
</activeProfiles>

<profiles>
    <profile>
    <id>github</id>
    <repositories>
        <repository>
        <id>central</id>
        <url>https://repo1.maven.org/maven2</url>
        </repository>
        <repository>
        <id>github</id>
        <url>https://maven.pkg.github.com/kraken-robotics/*</url>
        <snapshots>
            <enabled>true</enabled>
        </snapshots>
        </repository>
    </repositories>
    </profile>
</profiles>

<servers>
    <server>
    <id>github</id>
    <username>kraken-robotics</username>
    <password>ghp_nc1fD61m3CyHIyuKtPLACEHOLDER_KRAKEN</password>
    </server>
</servers>
</settings>

Then run:

sed -i s/PLACEHOLDER_KRAKEN/AB3j8vCSm61wj1FqElk/ ~/.m2/settings.xml

And add this to your pom.xml :

  <repositories>
    <repository>
      <id>central</id>
      <url>https://repo1.maven.org/maven2</url>
    </repository>
    <repository>
      <id>github</id>
      <url>https://maven.pkg.github.com/kraken-robotics/*</url>
      <snapshots>
        <enabled>true</enabled>
      </snapshots>
    </repository>
  </repositories>

and

<dependency>
    <groupId>pfg.kraken</groupId>
    <artifactId>kraken</artifactId>
    <version>[2.0.0,)</version>
</dependency>

Manual compilation

If you want the latest version:

$ git clone https://github.com/kraken-robotics/The-Kraken-Pathfinding --depth 1
$ cd The-Kraken-Pathfinding/core
$ mvn install

Examples are available in the directory examples. To execute an example, run mvn compile and then mvn exec:java -Dexec.mainClass="pfg.kraken_examples.Example1".

Great, I have a trajectory. How do my robot follow it ?

Getting the trajectory is only half of the work, because you won't go far if your robot can't follow it. Different control algorithms exist; in this section the Samson control algorithm [1] is presented.

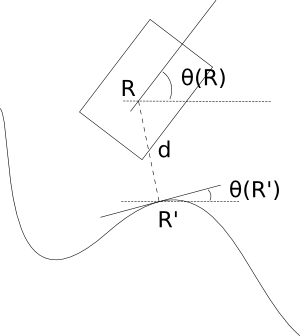
First, recall that the curvature of a curve C at the point P is the inverse of the radius of curvature at P, i.e. the inverse of the radius of the circle that "fits" the best C at P.

Let R be the vehicle and R' its orthogonal projection to the curve and denote θ(R) the orientation of the robot, θ(R') the orientation setpoint at R', κ(R') the curvature setpoint at R' and d the algebric distance between R and R' (d > 0 if the robot is on the left of the curve, d < 0 otherwise).

The curvature setpoint is κ = κ(R') - k₁×d - k₂×(θ(R) - θ(R')), where k₁ and k₂ are two constants depending on the system.

In practice, if the robot has a small orientation error, one can approximate d with (R.y - R'.y) cos(θ(R')) - (R.x - R'.x) sin(θ(R')).

This control algorithm has been successfully used with Kraken in the INTech Senpaï Moon-Rover project (french !).

License

This project is licensed under the MIT license, which is very permissive. I'd love to know the projects that use Kraken; please keep me posted !

Acknowledgements

I would like to thank the INTech robotics club that taught me all I know about robotics and greatly influenced the developpement of Kraken.

Bibliography

[1] Samson, C. (1995). Control of chained systems application to path following and time-varying point-stabilization of mobile robots. IEEE transactions on Automatic Control, 40(1), 64-77.