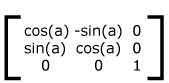-
Notifications
You must be signed in to change notification settings - Fork 87
Calculating 2d Matrices
JavaScript doesn’t have anything built-in to handle matrix calculations, however, there is a great library called Sylvester that makes matrices easy.
The CSS3 spec for 2d transformations lists out the common functions. But they didn’t just make them up out of thin air. Each function represents a specific matrix that is used to calculate coordinates on a new object. Apparently this is a common thing that math nerds have know for ages. The SVG spec has a great breakdown of how matrices work.
- rotate
- scale
- scaleX
- scaleY
- skew
- skewX
- skewY
- translate
- translateX
- translateY
transform: rotate(45deg) skewX(20deg);Combining transform functions together is equivalent to multiplying matrices together.
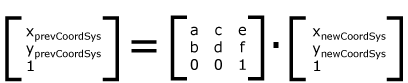
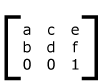
A 2d transformation matrix consists of 9 numbers arranged in a grid. The first two rows are used for the transformations and the last row is always 0, 0 1. As shown in the graph below, e and f are for translation which is conceptually similar to position: relative; where e is the same as left and f is the same as top.
| Sample Matrix | Translate Matrix |
|---|---|
|
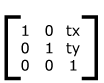 |
We’ll use Sylvester to do our matrix calculations and create an object that creates a matrix for each of the functions above. Things won’t get tricky until we try to combine our matrices.
// Creating matrices in Sylvester is easy
var matrix = $M([
[a, c, e],
[b, d, f],
[0, 0, 1]
]);
// if you're only doing one transformation, you can just apply it right away (you don't even need a matrix)
$('.example').css('-moz-transform', ''matrix(' + a + ', ' + b + ', ' + c + ', ' + d + ', ' + tx + 'px, ' + ty + 'px)');
// but you can use a matrix to calculate coordinates (which is useful is you're trying to fix IE)
// matrix.x is the matrix multipy function.
var coord = matrix.x($M([
[x],
[y],
[1]
]));
var newX = coord.e(1, 1),
newY = coord.e(2, 1);
As you can see, the main point of a matrix is to transform coordinates. So, if we input coords like 50, 50, we’ll get back what those coordinates are on the new object.
This function returns a matrix that will, well, rotate an object based on the number of degrees provided.
var Transform = {
rotate: function(deg) {
var rad = parseFloat(deg) * (Math.PI/180),
costheta = Math.cos(rad),
sintheta = Math.sin(rad);
var a = costheta,
b = sintheta,
c = -sintheta,
d = costheta;
return $M([
[a, c, 0],
[b, d, 0],
[0, 0, 1]
]);
},
...
};rotate(45) |
|---|
 |
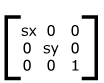
Scale returns a matrix for making an object bigger or smaller.
var Transform = {
...
scale: function (sx, sy) {
sx = sx || sx === 0 ? sx : 1;
sy = sy || sy === 0 ? sy : 1;
return $M([
[sx, 0, 0],
[0, sy, 0],
[0, 0, 1]
]);
},
scaleX: function (sx) {
return this.scale(sx);
},
scaleY: function (sy) {
return this.scale(1, sy);
},
...
};scale(0.5, 0.5) |
scaleX(0.5) |
scaleY(0.5) |
|---|---|---|
 |
 |
 |
| SkewX | SkewY |
|---|---|
 |
 |
Skew returns a matrix to tilt the object one way or the other.
var Transform = {
...
skew: function (degX, degY) {
var radX = parseFloat(degX) * (Math.PI/180),
radY = parseFloat(degY) * (Math.PI/180),
x = Math.tan(radX),
y = Math.tan(radY);
return $M([
[1, x, 0],
[y, 1, 0],
[0, 0, 1]
]);
},
skewX: function (deg) {
var rad = parseFloat(deg) * (Math.PI/180),
x = Math.tan(rad);
return $M([
[1, x, 0],
[0, 1, 0],
[0, 0, 1]
]);
},
skewY: function (deg) {
var rad = parseFloat(deg) * (Math.PI/180),
y = Math.tan(rad);
return $M([
[1, 0, 0],
[y, 1, 0],
[0, 0, 1]
]);
},
...
};skew(25, 25) |
skewX(25) x skewY(25)
|
|---|---|
 |
 |
skewX(25) |
skewY(25) |
|---|---|
 |
 |
Translate moves the object vertically or horizontally.
var Transform = {
...
translate: function (tx, ty) {
tx = tx ? tx : 0;
ty = ty ? ty : 0;
return $M([
[1, 0, tx],
[0, 1, ty],
[0, 0, 1]
]);
},
translateX: function (tx) {
return this.translate(tx);
},
translateY: function (ty) {
return this.translate(0, ty);
}
};translate(25, 25) |
translateX(25) |
translateY(25) |
|---|---|---|
 |
 |
 |
As mentioned above, doing only one transformation doesn’t really even require using the Sylvester matrix functions. But things get interesting when we try to do more than one thing. Here’s some notes:
- The CSS3 transform functions each represent a matrix similar to what’s shown above
- Using more than one function is the same as multiplying matrices together
- Order is actually important.
-moz-transform: rotate(45deg) skewX(25deg);is a different matrix from-moz-transform: skewX(25deg) rotate(45deg);
| rotate(45) skewX(25) | skewX(25) rotate(45) |
|---|---|
-moz-transform: matrix(0.707107, 0.707107, -0.377377, 1.036836, 0, 0); |
-moz-transform: matrix(1.036836, 0.707107, -0.377377, 0.707107, 0, 0); |
 |
 |
It’s actually pretty simple. Create at least two matrices and multiple them together as shown below.The particulars of the matrix.x() and matrix.e() functions are detailed in the Sylvester manual. But, the x() function multiplies two matrices and e(row, column) retrieves a number from the matrix where e(1, 1) is the first row and first column.
var rotate = Transform.rotate(45);
var skewX = Transform.skewX(25);
var matrix = rotate.x(skewX); // same as rotate(45deg) skewX(25deg)
var a = matrix.e(1,1),
b = matrix.e(2,1),
c = matrix.e(1,2),
d = matrix.e(2,2);
$('.example').css('-moz-transform', ''matrix(' + a + ', ' + b + ', ' + c + ', ' + d + ', 0, 0)');