Index

• Neural Network
  • The Perceptron
    • Perceptron learning Rule or Update Weights
  • Bias
• Activation Function
  • Sigmoid
• Optimizer
  • Gradient Descent
  • Stochastic Gradient Descent
  • Minibatch Stochastic Gradient Descent
  • Momentum
  • Adagrad
  • RMSProp
  • Adadelta
  • Adam
  • Learning Rate Scheduling

Deep Learning

• Deep learning is a more approachable name for an artificial neural network.
• The “deep” in deep learning refers to the depth of the network a.k.a Hidden layers. But an artificial neural network can also be very shallow.

Neural Network

• Neural networks are inspired by the structure of the cerebral cortex.
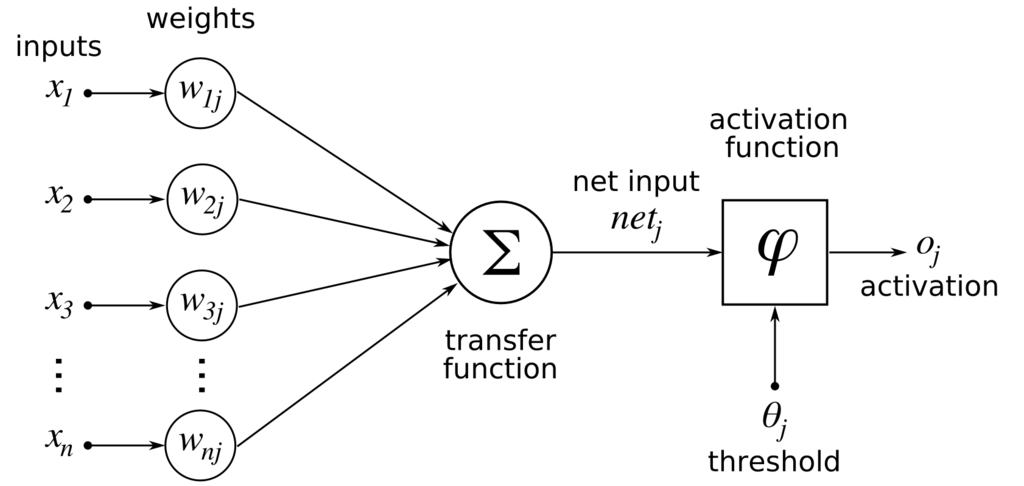
• At the basic level is the Perceptron, the mathematical representation of a biological neuron.
• Like in the cerebral cortex, there can be several layers of interconnected perceptrons.

The Perceptron

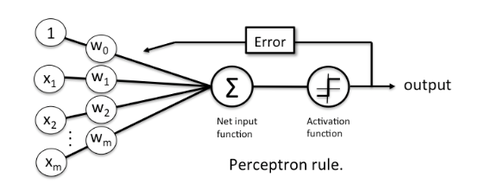
Its the simplest ANN architecture. It was invented by Frank Rosenblatt in 1957 and published as Rosenblatt, Frank (1958), The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain, Cornell Aeronautical Laboratory, Psychological Review, v65, No. 6, pp. 386–408. doi:10.1037/h0042519

Lets see the architecture shown below -

Perceptron

Common activation functions used for Perceptrons are (with threshold at $\large \theta$)-

$$\Large step(z) = \left \{ \begin{matrix} 0 & z< \theta\\ 1 & z\geq \theta \end{matrix} \right.$$

For all inputs and weights are like the followings-

$$\Large \begin{matrix*}[l] z &=& \ X_1W_1+X_2W_2+X_3W_3 \hspace{20pt} \large \textit{or we can write it as following- }\\ z &=& \sum\limits_{i=1}^{n} X_iW_i\\ \end{matrix*}$$

If we want to multiply W and X we will end up with two matrices-

• For multiplication of 2 matrices we need to have 1^st matrix column= 2^nd matrix row. That's why we take transpose of matrix W to W^T.

$$\Large z\ = \ X_1W_1+X_2W_2+X_3W_3 \tag 1 $$

$$\large \begin{matrix*}[l] \\ \\ W^{\top} = \begin{bmatrix*}[l] W_1&W_2 & W_3 \end{bmatrix*}_{n\times m} \hspace{20pt} X = \begin{bmatrix} X_1\\ X_2\\ X_3\\ \end{bmatrix}_{m \times n} \\ \begin{bmatrix*}[l] W_1 \\ W_2 \\ W_3 \\ \end{bmatrix*} \hspace{20pt} \begin{bmatrix} X_1\\ X_2\\ X_3\\ \end{bmatrix} = W^{\top} X \end{matrix*}$$

Derivation

• We are taking theta $\large \theta$ as the thrisold value-

$$\Large \sigma(z) = \begin{cases} +1 & if & z\geq \theta\\ -1 & if & z < \theta\\ \end{cases}$$

• Changing RHS to LHS

$$\Large \sigma(z) = \begin{cases} +1 & if & z - \theta \geq 0\\ -1 & if & z - \theta < 0\\ \end{cases}$$

• We are taking theta as $W_0X_0$ and $W_0X_0$ which is 'y intercept' or 'c' in y=mX+c

$$\Large \sigma(z) = \begin{cases} +1 & if & W^{\top}X+bias \geq 0\\ -1 & if & W^{\top}X+bias < 0\\ \end{cases}$$

Bias

• In $\large y=mX+c$ ,
  • c or bias helps the shifting from +ve to -ve and vice versa so that the output is controlled.
  • m or the slope helps the rotation.

• Bias effects the output as the following it change the output class +ve to -ve.

Perceptron learning Rule or Update Weights and Errors

• As we know error is (Predicted Value - Acctual Value) .

• A Neural Network back propagate and updates Weights and Bias.

• Now, the question is What would be the update weight?

• The update value for each input is not same as each input weight has different contribution to the final error.
• So the rectification of weight for each input would be different.

$$\Large{\color{Purple}w_{i,j} \leftarrow w_{i,j} + \eta(y_j - \hat{y_j})x_i}$$

Where:

$$\Large{\color{Purple}\begin{matrix*}[l] w_{i,j} &:& \textrm{connection weight between} \ \ i^{th} \textrm{ input neuron and } j^{th} \textrm{ output neuron} \\ x_i &:& i^{th}\textrm{ input value} \\ \hat{y_j} &:& \textrm{output of } \ j^{th}\ \textrm{ output } \\ y_j &:& \textrm{target output of }\ \ j^{th} \textrm{ output neuron} \\ \eta &:& \textrm{learning rate} \end{matrix*}}$$

It can also be written as for jth element of w vector

$$\Large{\color{Purple}\begin{matrix*}[l] w_j & = w_j + \Delta w_j\\ & \large where,\ \Delta w_j = \eta(y^{(i)} - \hat{y_j}^{(i)})x_j^{(i)} \end{matrix*} }$$

Update Weights can be written as

$$\Large{\color{Purple} W= W-\eta \frac{\partial e}{\partial w}}$$

Where

$$\Large{\color{Purple}\begin{matrix*}[l] W &=& Weight \\ \eta &=& Learning \ rate,\\ \partial e &=& Change \ in\ error, \\ \partial w &=& Change \ in\ weight\\ \end{matrix*}}$$

$$\large{\color{Purple}Here \hspace{10pt} (-\eta \frac{\partial e}{\partial w}) \ = \ \Delta W, \ \ \ From \ the\ above \ \ (W_j+\Delta W_j) }$$

Neural Network error Update Weights

• Suppose we have a Neural Network with 3 input layers and 2 hidden layers and we are using sigmoid as a activation function inside the hidden layer as well as in final weight calculation.

• Input buffers(that's why not having Bias, Input neuron would have Bias), Hidden layers, Output Neuron are like

$$\Large{\color{Purple}\begin{matrix*}[l] \textrm{Input Buffer} &=& X_1, X_2, X_3 \hspace{10pt} \textrm{ (No Bias, Input Neuron would have Bias)} \\ \textrm{W} &=& W_{i j}^{(z)} \hspace{10pt} \textrm{(i= the destination, j= the source, z = location number)}\\ \textrm{Bias} &=& b_i \\ \textrm{Weight Summation} &=& Z_i^{(z)} \hspace{10pt} \textrm{(i= Hidden or output neuron number, z = location)}\\ \widehat{Y} &=& \textrm{\ Final output}\\ \end{matrix*}}$$

• Hidden Layer weight calculation

• Final layer weight calculation

* Weight and Bias update rule-

Matrix representation of above diagrams

• Calculationin Hidden layers

$$\Large{\color{Purple} \begin{bmatrix} W_{11}&W_{12} & W_{13} \\ W_{21}& W_{22} & W_{23} \end{bmatrix}_{(2 \times 3)}* \begin{bmatrix} X_{1} \\ X_{2} \\ X_{3} \\ \end{bmatrix}_{(3 \times 1)} + \begin{bmatrix} b_{1} \\ b_{2} \\ \end{bmatrix} = \begin{bmatrix} Z_{1} \\ Z_{2} \\ \end{bmatrix} \to \begin{bmatrix} activation(Z_{1}) \\ activation(Z_{2}) \\ \end{bmatrix}\to \begin{bmatrix} a_{1} \\ a_{2} \\ \end{bmatrix} \hspace{10pt} or \hspace{10pt} \hat{Y} }$$

• Calculation in Output layer

$$\Large{\color{Purple} \begin{bmatrix} W_{11}& W_{12} \\ \end{bmatrix}_{(1 \times 2)}* \begin{bmatrix} a_{1} \\ a_{2} \end{bmatrix}_{(2 \times 1)} + \begin{bmatrix} b_{1} \\ \end{bmatrix} = \begin{bmatrix} Z_{1} \\ \end{bmatrix}\to \begin{bmatrix} activation(Z_{1}) \\ \end{bmatrix} \to \begin{bmatrix} a_{1} \\ \end{bmatrix} \hspace{10pt} or \hspace{10pt} \hat{Y}}$$

What are Neural networks?

Neural networks are set of algorithms inspired by the functioning of human brian. Generally when you open your eyes, what you see is called data and is processed by the Nuerons(data processing cells) in your brain, and recognises what is around you. That’s how similar the Neural Networks works. They takes a large set of data, process the data(draws out the patterns from data), and outputs what it is.

Neural Network Basics

• Neural networks were one of the first machine learning models.

• Deep learning implies the use of neural networks.

• The "deep" in deep learning refers to a neural network with many hidden layers.

• Neural networks accept input and produce output.

  • The input to a neural network is called the feature vector.
  • The size of this vector is always a fixed length.
  • Changing the size of the feature vector means recreating the entire neural network.
  • A vector implies a 1D array. Historically the input to a neural network was always 1D.
  • However, with modern neural networks you might see inputs, such as:-

• 1D Vector - Classic input to a neural network, similar to rows in a spreadsheet. Common in predictive modeling.

• 2D Matrix - Grayscale image input to a convolutional neural network (CNN).

• 3D Matrix - Color image input to a convolutional neural network (CNN).

• nD Matrix - Higher order input to a CNN.

Prior to CNN's, the image input was sent to a neural network simply by squashing the image matrix into a long array by placing the image's rows side-by-side. CNNs are different, as the nD matrix literally passes through the neural network layers.

Dimensions The term dimension can be confusing in neural networks. In the sense of a 1D input vector, dimension refers to how many elements are in that 1D array.

• For example a neural network with 10 input neurons has 10 dimensions.
• However, now that we have CNN's, the input has dimensions too.
• The input to the neural network will usually have 1, 2 or 3 dimensions. 4 or more dimensions is unusual.

---

• You might have a 2D input to a neural network that has 64x64 pixels.
• This would result in 4,096 input neurons.
• This network is either** 2D or 4,096D, **depending on which set of dimensions you are talking about!

Classification or Regression

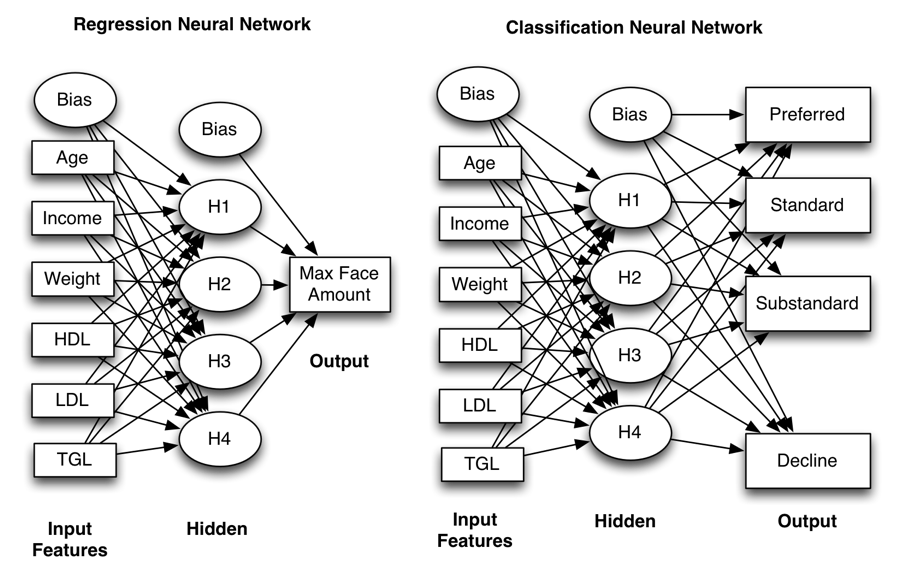
Like many models, neural networks can function in classification or regression:

• Regression - You expect a number as your neural network's prediction.
• Classification - You expect a class/category as your neural network's prediction.(the number of Input = The number of Output)

The following shows a classification and regression neural network:

• Notice that the output of the regression neural network is numeric and the output of the classification is a class.
• Regression, or two-class classification, networks always have a single output.
• Classification neural networks have an output neuron for each class.

---

The Calculation would be like-

• (I1W1+I2W2+B) = Weighted sum ;and it would be go through the Activation function
• Where 'I' is the input and 'W' is the weight.

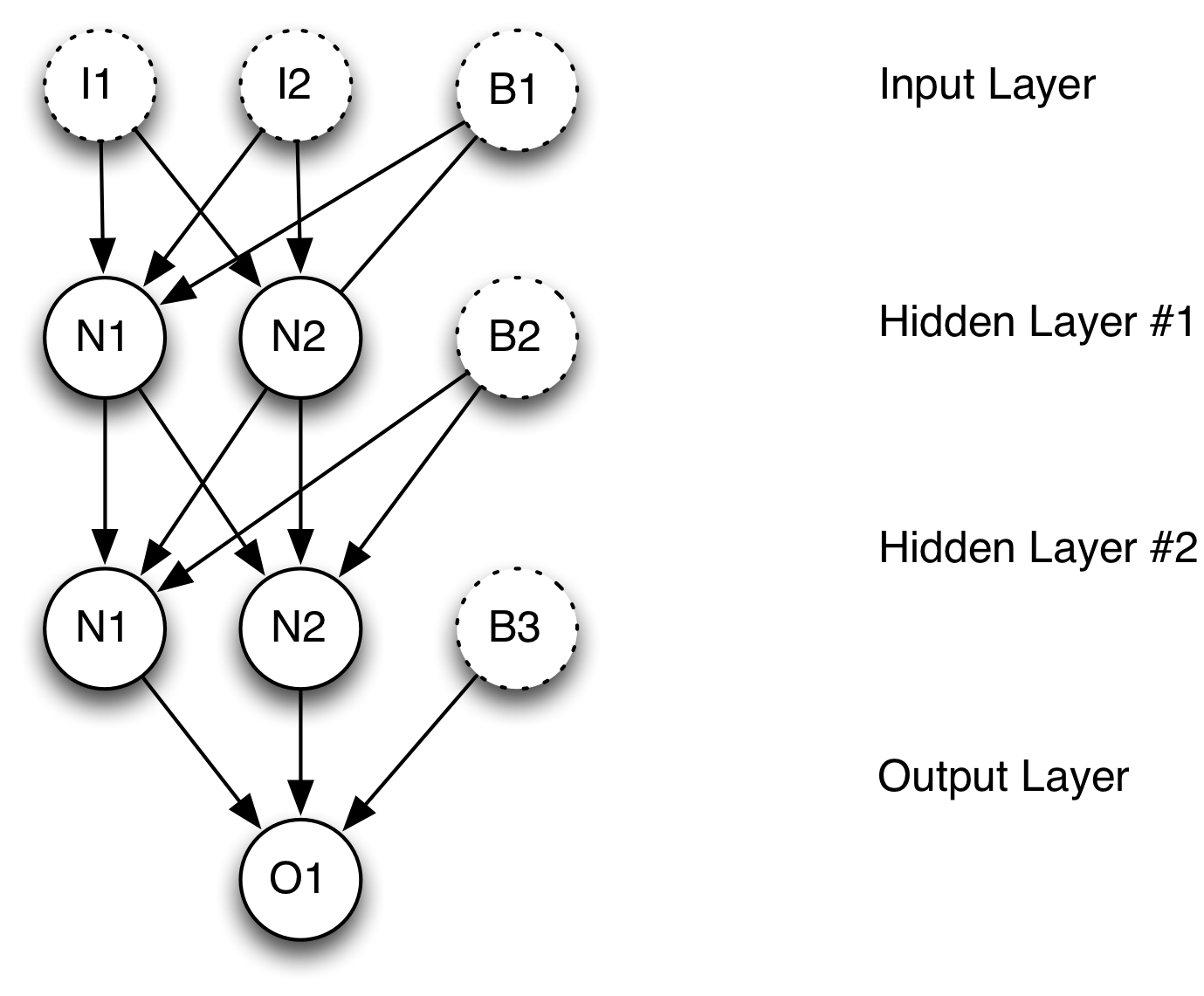
The following diagram shows a typical neural network:

There are usually four types of neurons in a neural network:

• Input Neurons - Each input neuron is mapped to one element in the feature vector.
• Hidden Neurons - Hidden neurons allow the neural network to abstract and process the input into the output.
• Output Neurons - Each output neuron calculates one part of the output.
• Context Neurons - Holds state between calls to the neural network to predict.
• Bias Neurons - Work similar to the y-intercept of a linear equation.

These neurons are grouped into layers:

• Input Layer - The input layer accepts feature vectors from the dataset. Input layers usually have a bias neuron.
• Output Layer - The output from the neural network. The output layer does not have a bias neuron.
• Hidden Layers - Layers that occur between the input and output layers. Each hidden layer will usually have a bias neuron.

Deep-Learning

Deep learning is a machine learning technique that teaches computers to do what comes naturally to humans: learn by example

Activation functions and what are it uses in a Neural Network Model?

Activation functions are really important for a Artificial Neural Network to learn and make sense of something really complicated and Non-linear complex functional mappings between the inputs and response variable.

• Their main purpose is to convert a input signal of a node in a A-NN to an output signal.
• A Neural Network without Activation function would simply be a Linear regression Model which has limited power and does not performs good most of the times.
• Also without activation function our Neural network would not be able to learn and model other complicated kinds of data such as images, videos , audio , speech etc

Why do we need Non-Linearities?

• Non-linear functions are those which have degree more than one and they have a curvature when we plot a Non-Linear function. Now we need a Neural Network Model to learn and represent almost anything and any arbitrary complex function which maps inputs to outputs.
• Also another important feature of a Activation function is that it should be differentiable. We need it to be this way so as to perform backpropogation optimization strategy while propogating backwards in the network to compute gradients of Error(loss) with respect to Weights and then accordingly optimize weights using Gradient descend or any other Optimization technique to reduce Error.

Most popular types of Activation functions -

Sigmoid or Logistic Tanh — Hyperbolic tangent ReLu -Rectified linear units

Back-propagation

What is error?

• Error or loss is the difference between the actual value and the expected value.
• In deep Neural Net we adding up the Waights in every layer and at the end (or between-ReLu for hidden layer)we calculate all the waightes with a Activation function.
• The main perpose of back propagation is to go back in the Neural Network and modify the weights

• Backpropagation is a technique used to train certain classes of neural networks – it is essentially a principal that allows the machine learning program to adjust itself according to looking at its past function.
• Backpropagation is sometimes called the “backpropagation of errors.”
• Backpropagation as a technique uses gradient descent: It calculates the gradient of the loss function at output, and distributes it back through the layers of a deep neural network. The result is adjusted weights for neurons.

Bibliography:

• https://medium.com/@purnasaigudikandula/recurrent-neural-networks-and-lstm-explained-7f51c7f6bbb9
• https://mattmazur.com/2015/03/17/a-step-by-step-backpropagation-example/
• Andrew Ng- Coursera