CTRNN

Python package that implements Continuous Time Recurrent Neural Networks (CTRNNs)

See Beer, R.D. (1995). On the dynamics of small continuous-time recurrent neural networks. Adaptive Behavior 3:469-509. for a study of CTRNNs.

Using this repo in conjunction with StochSearch allows you to optimize CTRNNs to perform different tasks. Stochsearch uses Python's multiprocessing framework to parallelize population based stochastic search optimization methods.

You can also find a Tensorflow version of building and implementing a population of CTRNNs here. Refer to this same repo for optimizing CTRNNs using Tensorflow on a GPU.

Installation instructions

    $ pip install CTRNN

Requirements: numpy, scipy

Citing

    @misc{Candadai_CTRNN_2020,
    author = {Candadai, Madhavun},
    month = {3},
    title = {CTRNN},
    url = {https://github.com/madvn/CTRNN},
    year = {2020}
    }

Using the package

Importing the CTRNN package:

    from CTRNN import CTRNN

Creating a CTRNN object:

    cns = CTRNN(network_size,step_size=0.1) 

weights are initialized randomly; gains, time-constants and biases are set to 1

Setting gain for neuron i:

    cns.gains[i] = 1 

where i is in range [0,network_size)

Setting gain for all neurons:

    cns.gains = [1,2,3,..] 

with list of size=network_size

Setting biases and time-constants (taus) is similar

    cns.biases
    cns.taus

Setting weights to neuron i from neuron j:

    cns.weights[i,j] = 3 

where i,j in range [0,network_size)

Setting weights as a matrix:

    from scipy.sparse import csr_matrix
    cns.weights = csr_matrix(weights_matrix) 

where weights_matrix is of size=network_sizeXnetwork_size

Euler stepping the network:

    cns.euler_step(external_inputs)

where external_inputs is a list of size=network_size

Accessing/Setting output of neuron i:

    print(cns.outputs[i]) 
    cns.outputs[i] = 0.5

where i in range [0,network_size) and output in range [0,1]

Accessing/Setting output of all neurons:

    print(cns.outputs)
    cns.outputs = [0.5,0.75,0.4]

where list is of size=network_size

Same as above for states

    cns.states

where state values can range in (-inf,inf)

Randomizing states/outputs

    cns.randomize_states(ub,lb) 

upper bound and lower bound in range (-inf,inf)

    cns.randomize_outputs(ub,lb) 

upper bound and lower bound in [0,1]

Example

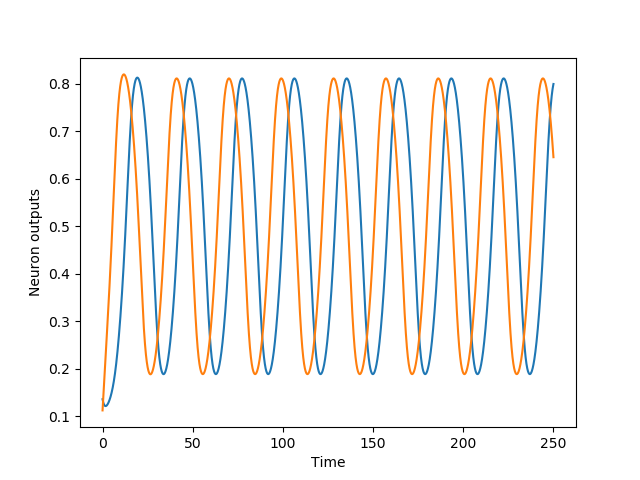
The following code creates a 2-neuron CTRNN sinusoidal oscillator, See demo folder::

    # imports
    import numpy as np
    import matplotlib.pyplot as plt
    # importing the CTRNN class
    from CTRNN import CTRNN

    # params
    run_duration = 250
    net_size = 2
    step_size = 0.01

    # set up network
    network = CTRNN(size=net_size,step_size=step_size)
    network.taus = [1.,1.]
    network.biases = [-2.75,-1.75]
    network.weights[0,0] = 4.5
    network.weights[0,1] = 1
    network.weights[1,0] = -1
    network.weights[1,1] = 4.5

    # initialize network
    network.randomize_outputs(0.1,0.2)

    # simulate network
    outputs = []
    for _ in range(int(run_duration/step_size)):
        network.euler_step([0]*net_size) # zero external_inputs
        outputs.append([network.outputs[i] for i in range(net_size)])
    outputs = np.asarray(outputs)

    # plot oscillator output
    plt.plot(np.arange(0,run_duration,step_size),outputs[:,0])
    plt.plot(np.arange(0,run_duration,step_size),outputs[:,1])
    plt.xlabel('Time')
    plt.ylabel('Neuron outputs')
    plt.show()

Output: