Introduction

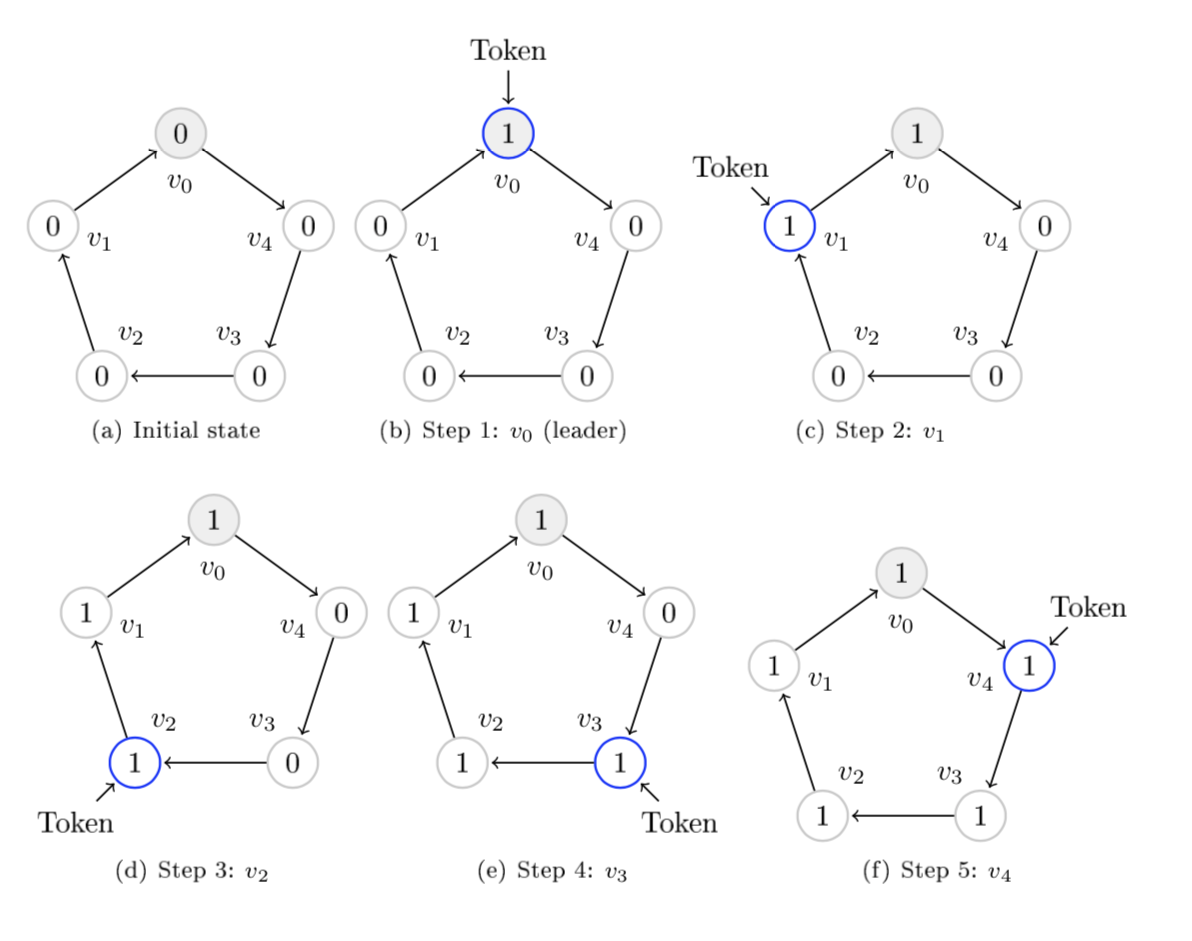
Dijkstra presented a self stabilizing token ring using guarded commands in his paper paper on self stabilization[1]. Starting from an arbitrary initial state it will stabilize in a finite number of steps such that exactly one node holds the token. Each node v in the graph knows it's clockwise neighbors as it's parent p and node v_0 is the leader. The value of node v is denoted $S(v)$ and is eventually always in {0, ..., n-1} where n is the number of nodes in the graph. The token passes from a parent to child, traveling the graph counter-clockwise.

If we look at a sample graph with 5 nodes where all initially have the value 0. The system is stable and v_0 has the token as $S(v_0) = S(p_{v_0})$.

Rebeca model

The mapping between the algorithm and the Rebeca[2] modeling language is fairly straight forwards. We create one reactive class for the nodes and once rebec from this class for each node in the graph. However instead of the nodes knowing their parent we invert the relations such that each node knows it's child. Every time a node changes it's value it will send the new value to it's child. In order to verify the model from every initial state we initialize the value with a non-deterministically selected value in the range {0,...,n-1}.

For this example we would like to verify three properties

1. The leader will eventually have a value that no other node in the graph has.
2. The system will never deadlock
3. Eventually every node will receive the token, i.e. no node will suffer starvation.

Conclusion

The self stabilizing token ring is a well known algorithm but is however difficult to prove for asynchronous systems. The Rebeca code is small, simple and descriptive which we believe is one of Rebeca's strengths. We are able to verify the algorithm in matter of seconds even though the state space is very large ($n^n=5^53125$ initial states). It is assumed that eventually all messages will be delivered which could be implemented using acknowledgements or simply periodically sending the values regardless of whether it has changed.

References

1. Edsger W. Dijkstra. Self stabilization in spite of distributed control, Comm. ACM, 1974.
2. Marjan Sirjani, Ali Movaghar, Amin Shali, and Frank S. de Boer. Modeling and verification of reactive systems using rebeca. Technical report, 2004.