MarriageMarkets

The MarriageMarkets package currently provides two marriage market models as Julia types:

• StaticMatch: computes the equilibrium of the static frictionless marriage market model from "Who Marries Whom and Why" (Choo & Siow, 2006).
• SearchMatch: computes the equilibrium of variants on the search and matching model from "Assortative Matching and Search" (Shimer & Smith, 2000) and the empirical extension in "Marriage Gains" (Goussé, 2014).

SearchMatch also allows for inflows of new singles as well as deaths.

Installation

In a Julia REPL, enter pkg mode (by pressing ]) and run:

(v1.0) pkg> add MarriageMarkets

Julia version 1.0 or higher is required (installation instructions here).

Usage

As SearchMatch supports a number of model variants, there are specific constructors for the two main types:

• SearchClosed: closed-system where agents cycle between singlehood and marriage
• SearchInflow: steady-state population is determined by exogenous inflows and type-specific death rates

All models support both unidimensional and multidimensional agent types. To specify a multidimensional type space, use a Vector of Vectors, e.g., [[1,1.5,1.7], [0,1]]

Examples

Here are some simple examples of solving models with unidimensional types. I use Gadfly to plot the resulting equilibrium objects.

Static model

using MarriageMarkets
using Gadfly

n = 50 # number of types
Θ = collect(range(0.1, stop=1.0, length=n)) # type space vector
m = ones(n) ./ n # uniform population measures
f(x,y) = x*y # marital surplus function (per capita)

static_mgmkt = StaticMatch(Θ, Θ, m, m, f)

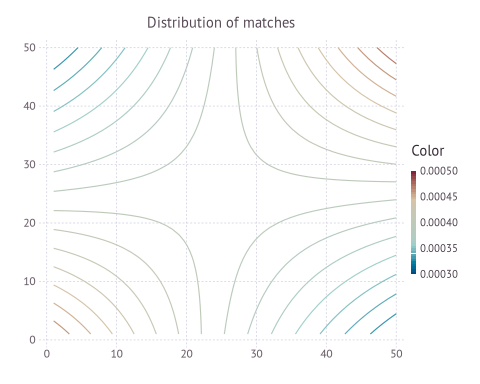
plot(z=static_mgmkt.matches, Geom.contour, Guide.title("Distribution of matches"))

The saddle shape indicates positive assortative matching, as expected, due to the supermodular production function f(x,y) = x*y.

Search model

The example below solves a search model with inflows and death. Then I plot the probabilities of match formation conditional on meeting.

using MarriageMarkets
using Gadfly

λ, δ = 500.0, 0.05 # arrival rates of meetings and divorce shocks
r = 0.05 # discount rate
σ = 1 # variance of Normally distributed match-specific productivity shocks
n = 50 # number of types
Θ = collect(range(0.1, stop=1.0, length=n)) # type space vector
f(x,y) = x*y # marital production function

γ = ones(n) ./ n # uniform inflows
ψ = ones(n) # uniform death rates

search_mgmkt = SearchInflow(λ, δ, r, σ, Θ, Θ, γ, γ, ψ, ψ, f)

plot(z=search_mgmkt.α, Geom.contour, Guide.title("Match probability conditional on meeting"))

Testing

In a Julia REPL session, enter pkg mode and run test MarriageMarkets.