Read this in other languages: english.
En mathématiques, l'algorithme d'Euclide est un algorithme qui calcule le plus grand commun diviseur (PGCD) de deux entiers, c'est-à-dire le plus grand entier qui divise les deux entiers, en laissant un reste nul. L'algorithme ne connaît pas la factorisation de ces deux nombres.
Le PGCD de deux entiers relatifs est égal au PGCD de leurs valeurs absolues : de ce fait, on se restreint dans cette section aux entiers positifs. L'algorithme part du constat suivant : le PGCD de deux nombres n'est pas changé si on remplace le plus grand d'entre eux par leur différence. Autrement dit, pgcd(a, b) = pgcd(b, a - b). Par exemple, le PGCD de 252 et 105 vaut 21 (en effet, 252 = 21 × 12 and 105 = 21 × 5), mais c'est aussi le PGCD de 252 - 105 = 147 et 105. Ainsi, comme le remplacement de ces nombres diminue strictement le plus grand d'entre eux, on peut continuer le processus, jusqu'à obtenir deux nombres égaux.
En inversant les étapes, le PGCD peut être exprimé comme une somme de
les deux nombres originaux, chacun étant multiplié
par un entier positif ou négatif, par exemple 21 = 5 × 105 + (-2) × 252.
Le fait que le PGCD puisse toujours être exprimé de cette manière est
connue sous le nom de Théorème de Bachet-Bézout.
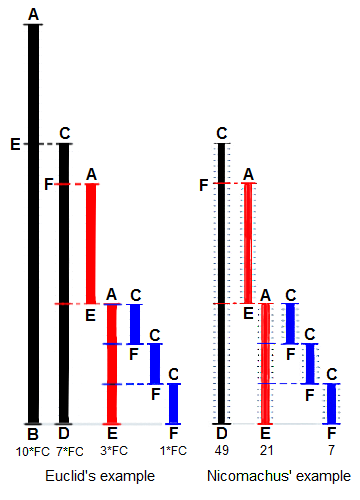
La Méthode d'Euclide pour trouver le plus grand diviseur commun (PGCD)
de deux longueurs de départBA et DC, toutes deux définies comme étant
multiples d'une longueur commune. La longueur DC étant
plus courte, elle est utilisée pour « mesurer » BA, mais une seule fois car
le reste EA est inférieur à DC. EA mesure maintenant (deux fois)
la longueur la plus courte DC, le reste FC étant plus court que EA.
Alors FC mesure (trois fois) la longueur EA. Parce qu'il y a
pas de reste, le processus se termine par FC étant le « PGCD ».
À droite, l'exemple de Nicomaque de Gérase avec les nombres 49 et 21
ayan un PGCD de 7 (dérivé de Heath 1908: 300).
Un de rectangle de dimensions 24 par 60 peux se carreler en carrés de 12 par 12,
puisque 12 est le PGCD ed 24 et 60. De façon générale,
un rectangle de dimension a par b peut se carreler en carrés
de côté c, seulement si c est un diviseur commun de a et b.
Animation basée sur la soustraction via l'algorithme euclidien.
Le rectangle initial a les dimensions a = 1071 et b = 462.
Des carrés de taille 462 × 462 y sont placés en laissant un
rectangle de 462 × 147. Ce rectangle est carrelé avec des
carrés de 147 × 147 jusqu'à ce qu'un rectangle de 21 × 147 soit laissé,
qui à son tour estcarrelé avec des carrés 21 × 21,
ne laissant aucune zone non couverte.
La plus petite taille carrée, 21, est le PGCD de 1071 et 462.