Skip to content

Latest commit

 

History

History
51 lines (42 loc) · 2.21 KB

README.md

File metadata and controls

51 lines (42 loc) · 2.21 KB
Raw

Travelling salesman problem

Implemnetation of Approximate Local Search for the TSP.

This is is an implementation of Jon Bentley's (http://en.wikipedia.org/wiki/Jon_Bentley) 2-Opt search for the TSP with "dont look bits". I aim for this (java) implementation to be as efficient as possible).

Originally, this was as an implementation of GLS: http://en.wikipedia.org/wiki/Guided_Local_Search

However.. GLS requires a matrix to store (N^2-N)/2 edge penalties which is O(N^2) for N cities. As such, GLS is limited to instances <= sqrt((81024102410248)/32) = 46,340 cities on a machine with 8G free memory.

For now, this is the FLS (Fast Local Search) component of GLS (with improvements.) which is actually a first improvement (as opposed to greedy) version of the approximate 2-Opt heuristic described by Bentley^. See http://pubsonline.informs.org/doi/abs/10.1287/ijoc.4.4.387

test:

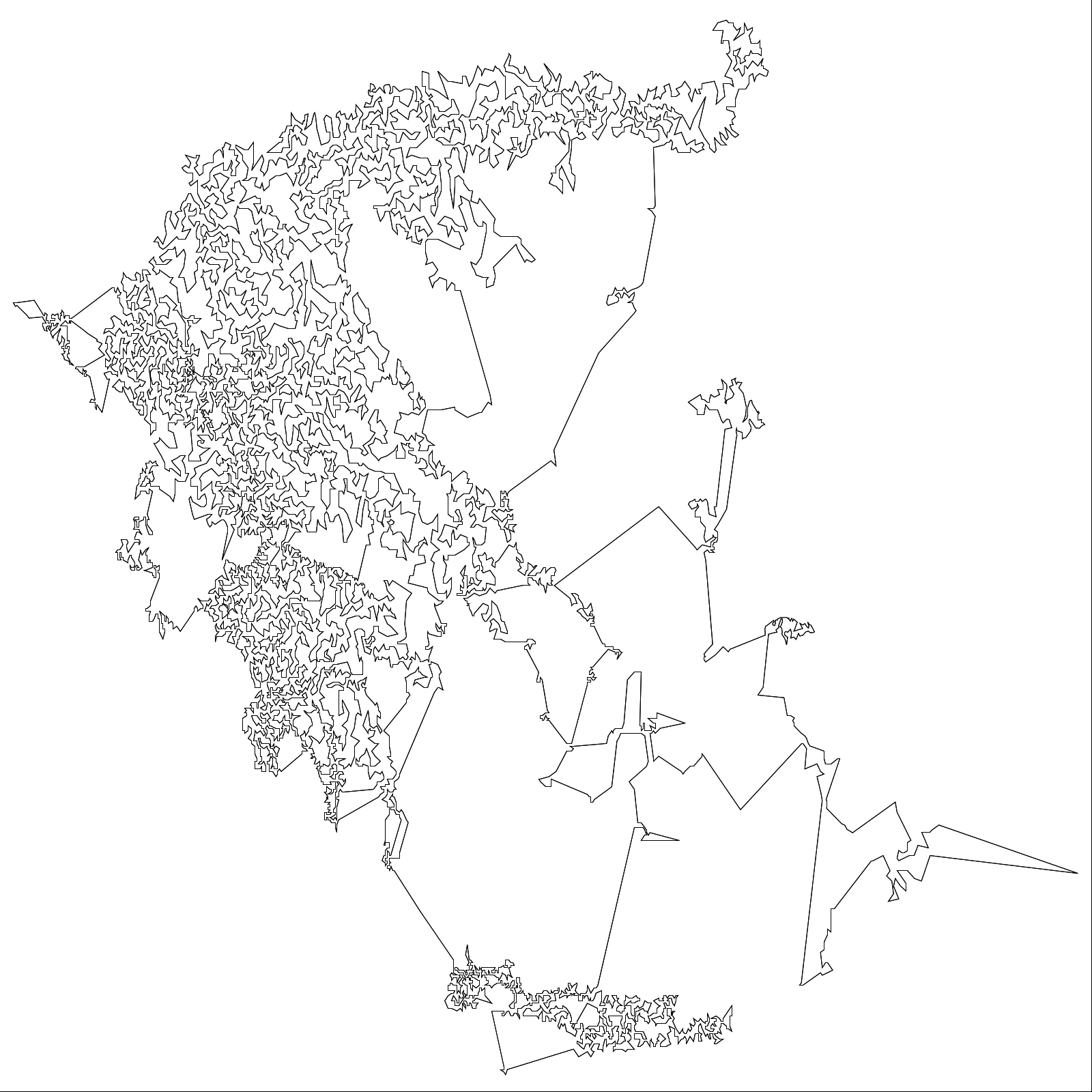
tour of 9,882 cities in greece. known optimal = 300,899.

phil@Eris:~/tsp$ ./run.sh data/gr9882.tsp /tmp/points.out
tour length = 340852.95 optimisation time = 2.84 seconds.
phil@Eris:~/tsp$ ./post-process.sh /tmp/points.out
phil@Eris:~/tsp$ convert /tmp/out.png -flip /tmp/out-flip.png
phil@Eris:~/tsp$ convert /tmp/out-flip.png -rotate -90 out.png

alt tag

notes

  • GLS, due to its dependency on distance matrix and penalty matrix is not capable of searching large problems. should look at alternative ways to store penalty term. pheramone? actually, the GLS algorithm seems to assume an infinite penalty matrix = to the distance matrix. it is easy to get rid of the distance matrix, as in this code. however the GLS penalty matrix must persist: GLS lets FLS do all of the work, then penalises. GLS also claims that the implementation details of the underlying local search algorithm do not mater. however, this is not the case, since GLS relies on a distance matrix which is "augmented".
  • checking if ab < ac && cd < bd in moveCost(...) before doing the 4 sqrt()s is a massive performance gain. tried an LRU cache for distances, inlining lots of code, precomputing sqrts: with little improvement.