Mathematical model of a multiple pendulum/cart system

[BystrickyK]

Definition of the Lagrangian and Rayleigh dissipation. The Lagrangian along with the Rayleigh dissipation function are then rewritten into MATLAB, where the system's Lagrange equations are analytically solved and transformed into state-space form.

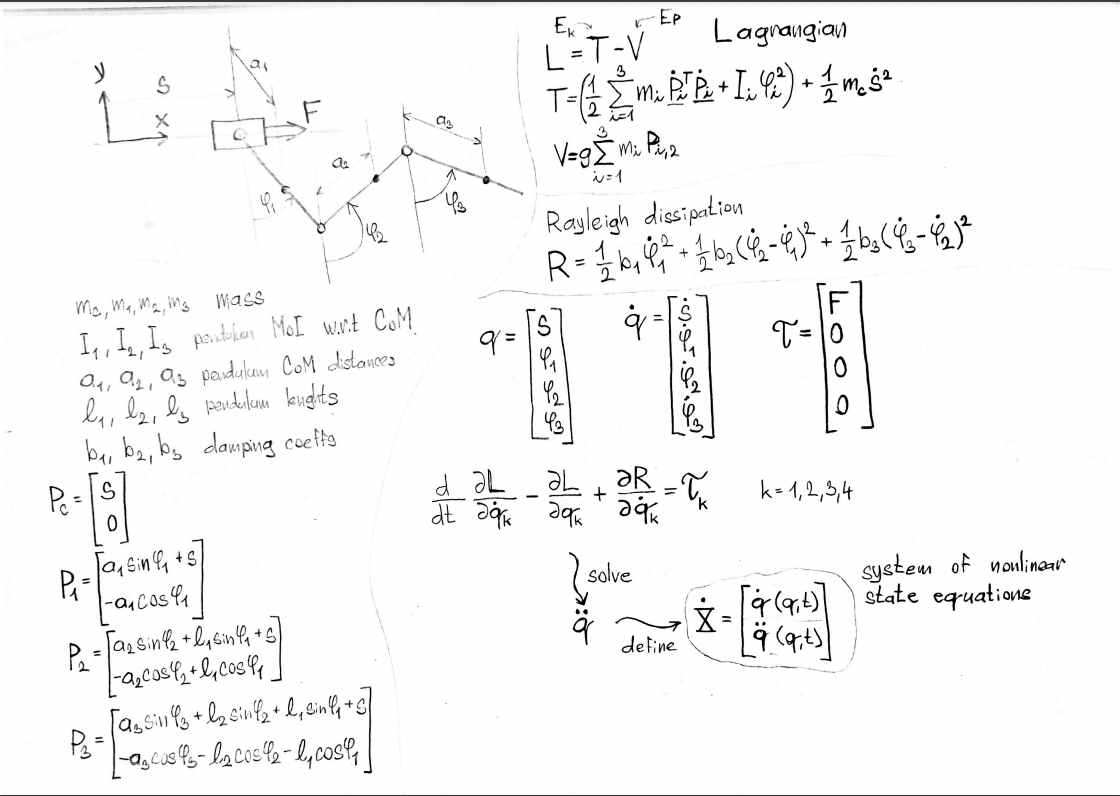
Resulting equations for the angular accelerations of the pendulums are massive. Here is the ODE describing the acceleration of the first pendulum (there's a mistake, Phi_1 on the left hand side should have two dots instead of one):

The analytical state-space derivative equations are then automatically rewritten into MATLAB ODE functions, so they can be numerically solved in time. A little manual adjustment has to be done to the MATLAB ODE functions to define the system input (cart acceleration) as a time-variant function, so the system can be simulated with external input forcing. The system parameters are then guessed, and the system is simulated and animated to visually verify the model.

No forcing:

With forcing, input signal is set as a random walk signal (although it's constrained, so the cart doesn't move too far from 0 and to make sure the cart acceleration is below ~4G):
https://user-images.githubusercontent.com/55796835/109891105-c3f5e280-7c88-11eb-9492-7fb70c044870.mp4

I also simplified the model by removing two of the pendulums, the state equations are much smaller and therefore better for testing the identification method.
https://user-images.githubusercontent.com/55796835/109821129-f62a2480-7c35-11eb-84bc-1b48f13ad1b2.mp4