Optical Tracker Algorithms
The PSMove sphere position relative to the camera(s) can be determined using one of several different techniques. This Wiki page describes some of those techniques.
- Common Steps
- Analytic solution after ellipse fitting
- Cone fitting
- 2 or more cameras with overlapping frustums
- Other Information
TODO...
This is the algorithm I used in my fork of psmoveapi. The sphere can be thought of as a base of a cone whose vertex is at the camera focal point. The camera's sensor plane can be thought of as a slice through the cone, creating an ellipse. We fit an ellipse to the blob. Then we can determine the sphere's 3D position by using similar triangles to relate known quantities (camera FOV, focal length, ellipse centre, major and minor axes) to unknown quantities. The image below presents the variables then the code below that outlines how to solve for unknown variables.
![]()
// TODO: OpenCV3 C++ synatx
// Fit an ellipse to our blob
CvBox2D ellipse = cvFitEllipse2(blob);
// Fill in known variables
f_px = camera_focal_length;
X_px = ellipse.center.x;
Y_px = ellipse.center.y;
A_px = ellipse.size.width / 2;
// If we are using a region of interest, correct for its offset.
X_px += roi_x;
Y_px += roi_y;
// Change image origin from top-left to middle-middle
X_px -= frame_width / 2;
Y_px = frame_height - Y_px;
// Derived values
// The length of the line from image centre to ellipse centre.
L_px = sqrt(X_px*X_px + Y_px*Y_px);
// The green triangle goes from the camera pinhole (at origin)
// to 0,0,f_px (centerpoint on focal plane),
// to the center of the sphere on the focal plane (x_px, y_px, f_px)
// The orange triangle extends the green triangle to go from pinhole,
// to the middle of the sensor image, to the far edge of the ellipse (i.e. L_px + a_px)
// Theta, the angle in the green triangle from the pinhole
// to the center of the sphere on the image, off the focal axis:
// theta = atan(k), where
k = L_px / f_px;
// theta + alpha, the angle in the green+orange triangle
// from the pinhole to the far edge of the ellipse, off the focal axis:
// theta + alpha = atan( j ), where
float j = (L_px + A_px) / f_px;
// Re-arranging for alpha:
// alpha = atan(j) - atan(k);
// Difference of atans (See 5.2.9 here:
// http://www.mathamazement.com/Lessons/Pre-Calculus/05_Analytic-Trigonometry/sum-and-difference-formulas.html )
// atan(j) - atan(k) = atan(l), where
float l = (j - k) / (1 + j*k);
// Thus, alpha = atan(l)
// The red+purple+orange triangle goes from camera pinhole,
// to the edge of the sphere, to the center of the sphere.
// sin(alpha) = R_cm / D_cm;
// sin(atan(l)) = R_cm / D_cm;
// sin of arctan (http://www.rapidtables.com/math/trigonometry/arctan/sin-of-arctan.htm )
// sin(atan(l)) = l / sqrt( 1 + l*l )
// R_cm / D_cm = l / sqrt( 1 + l*l )
// Solve for D:
float D_cm = SPHERE_RADIUS_CM * sqrt(1 + l*l) / l;
// We can now use another pair of similar (nested) triangles.
// The outer triangle (blue+purple+orange) has base L_cm, side Z_cm, and hypotenuse D_cm.
// The inner triangle (blue + some orange) has base L_px, size f_px, and hypotenuse D_px.
// From the larger triangle, we get sin(gamma) = Z_cm / D_cm;
// From the smaller triangle, we get tan(gamma) = f_px / L_px,
// or gamma = atan( f_px / L_px );
// then sin(gamma) = sin( atan( f_px / L_px ) ) = Z_cm / D_cm;
// Again, using the sin-of-arctan identity
// sin( atan( f_px / L_px ) ) = fl / sqrt( 1 + fl*fl ) = Z_cm / D_cm, where
float fl = f_px / L_px; // used several times.
// Solve for Z_cm
Z_cm = D_cm * fl / sqrt( 1 + fl*fl);
// Use a pair of similar triangles to find L_cm
// 1: blue + purple + orange; tan(beta) = z_cm / L_cm
// 2: inner blue + some orange; tan(beta) = f_px / L_px
// Solve for L_cm
float L_cm = Z_cm * k;
// We can now use the pair of gray triangles on the x-y plane to find x_cm and y_cm
X_cm = L_cm * X_px / L_px;
Y_cm = L_cm * Y_px / L_px;Warning: The below algorithm is not exactly what we're using. It's close but there are some critical differences. You can see the production code here.
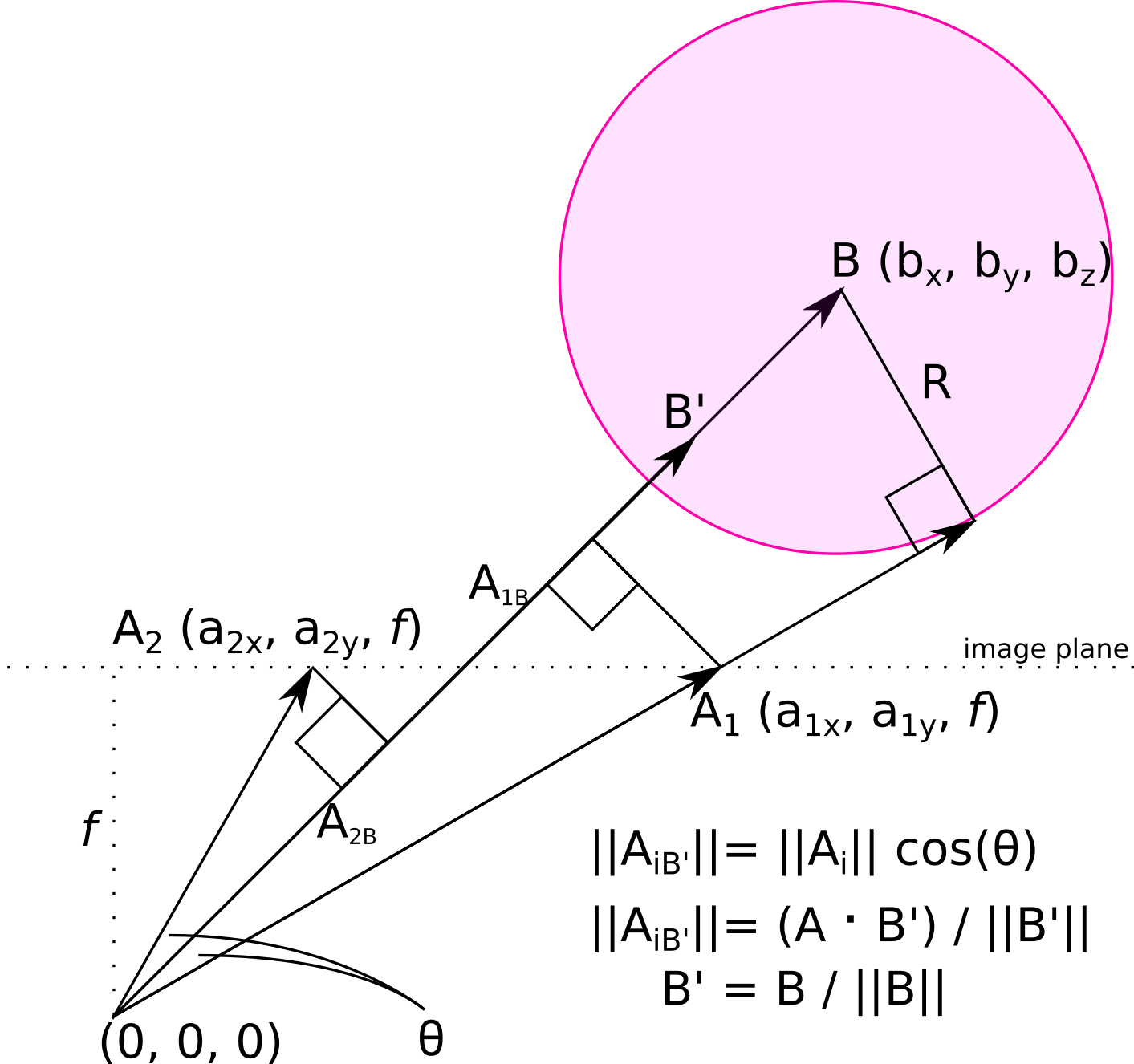
The PSMove sphere can be thought of as the base of a cone nappe with its apex at the camera's focal point (0, 0, 0). Let B (b_x, b_y, b_z) be the vector from the camera focal point to the middle of the sphere. B' is the unit vector parallel to B.
The PSMove sphere appears as a blob on the camera image. This blob can be thought of as a slice through the cone. Every point on the contour of the blob is an end point of a vector, A (a_x, a_y, a_z), from the origin, that lies on the surface of the cone. a_z = the camera's focal length. a_x and a_y are the coordinates of the points on the contour.
Let theta = the angle between B and A. This is half the opening angle (a.k.a. aperture) of the cone.
The projection of A onto B', denoted by A_B', has magnitude |A_B'| = |A| cos(theta). A_B is also the dot product of A.B' normalized by |B'|. Here, |B'| = 1.
A.B' = |A| * cos(theta)
Expanding this out and collecting terms gives the following:
a = B'_x^2 - cos(0)^2
b = B'_y^2 - cos(0)^2
c = 2 * B'_x * B'_y
d = 2B'_x * B'_z * A_z
e = 2B'_y * B'_z * A_z
f = (B'_z^2 - cos(0)^2) * A_z^2
ax^2 + by^2 + cxy + dx + ey + f = 0 // Equation of ellipse
Then, with at least 6 points on our contour, we do a least squares fit to solve for a, b, c, d, e, f. With some algebra we can figure out B' and k = cos(theta). Finally...
|B| = R / sin(acos(k)) = R / sqrt(1-k^2)
B = |B| * B'
Each optical tracker only needs to get the 2D position of the object. Where will these be merged? In the controller? Then the controller needs knowledge of the tracking solution, which seems bad. Maybe we need a single 'tracker' to represent a combination of cameras?
TODO: Links to sensor fusion