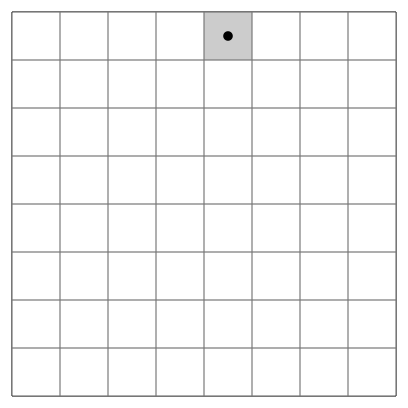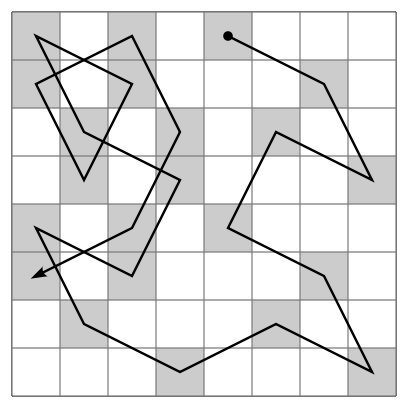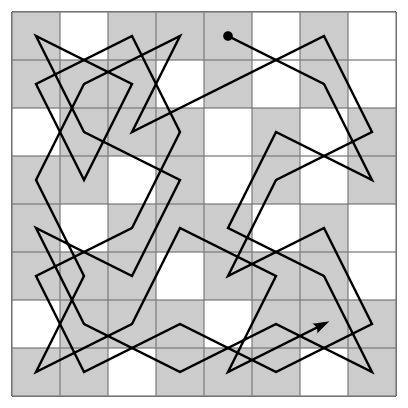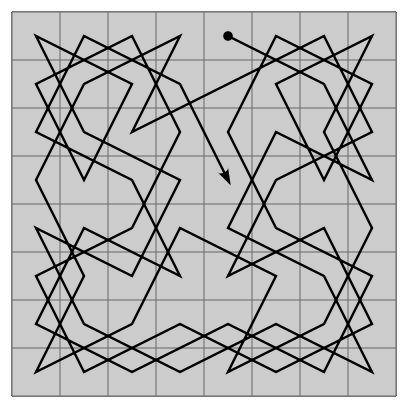
A knight's tour is a sequence of moves of a knight on a chessboard such that the knight visits every square only once. If the knight ends on a square that is one knight's move from the beginning square (so that it could tour the board again immediately, following the same path), the tour is closed, otherwise it is open.
The knight's tour problem is the mathematical problem of
finding a knight's tour. Creating a program to find a knight's
tour is a common problem given to computer science students.
Variations of the knight's tour problem involve chessboards of
different sizes than the usual 8×8, as well as irregular
(non-rectangular) boards.
The knight's tour problem is an instance of the more general Hamiltonian path problem in graph theory. The problem of finding a closed knight's tour is similarly an instance of the Hamiltonian cycle problem.
An open knight's tour of a chessboard.
An animation of an open knight's tour on a 5 by 5 board.