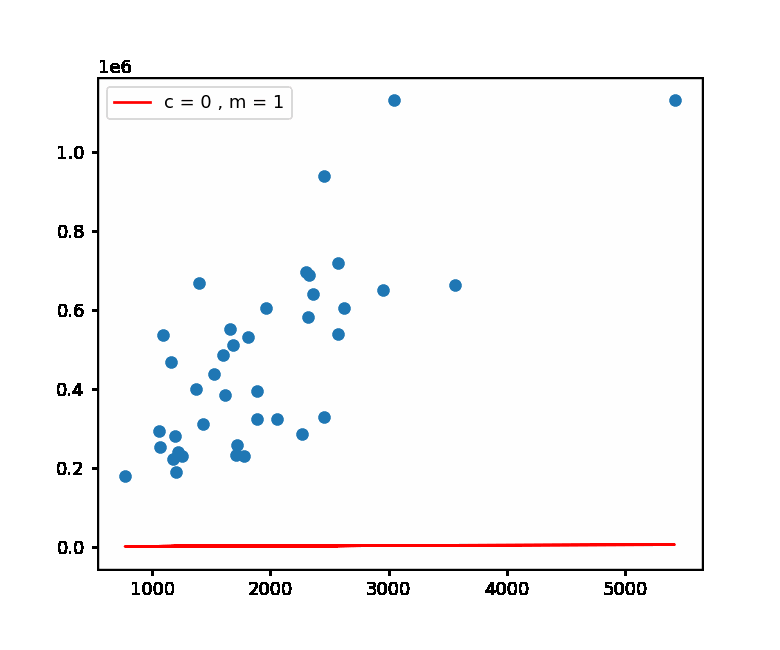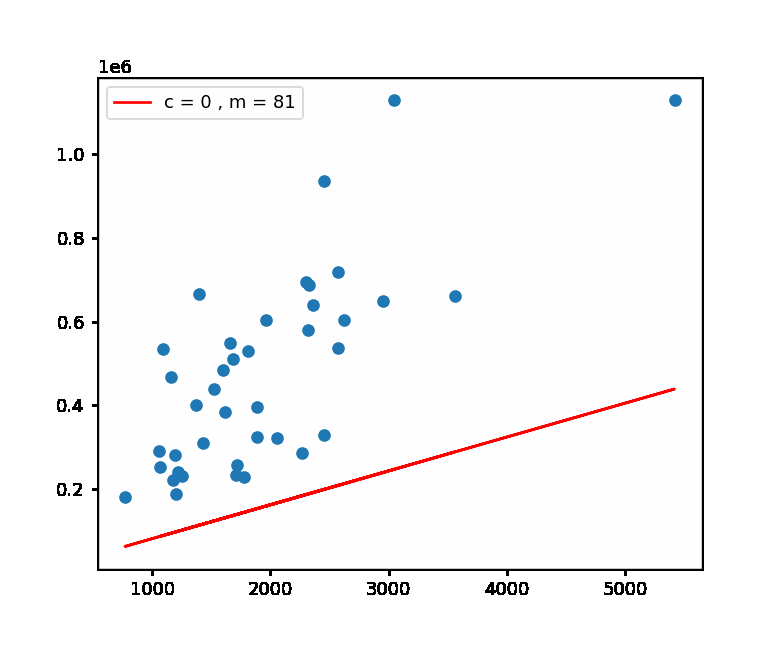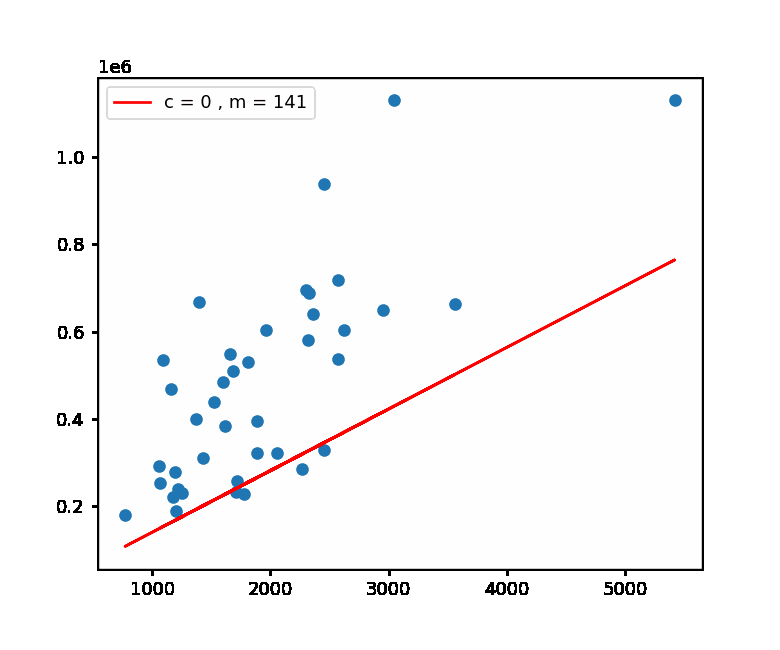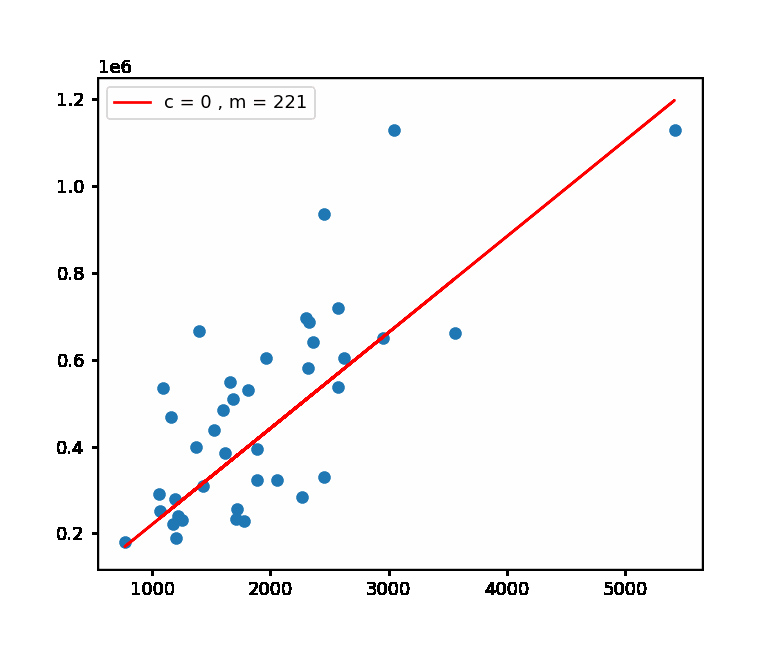
Implementation of Gradient Descent with Linear Regression model using Python on the Housing Prices Dataset.
Gradient Descent is an optimization algorithm that works iteratively and aims to find the minimum value of a convex function with respect to a set of parameters. This process is used in multiple machine learning algorithms and processes.
Let's try to understand Gradient Descent using a real life example,
Let's move back to our school days ,
My friends and I always used to argue that who is going to treat everyone in the canteen, and to put to rest this huge issue we often used to have a Paper Ball competition .
In this paper ball competition all were given a definite number of paper balls and the objective was to throw as many paper balls in dustbin as one possibly can. The number of balls thrown successfully in the dustbin was that player's score.
The friend with the lowest score had to treat everyone that day. Sounds like a cool solution right?
Now suppose you and your friends are playing this game. It's your turn and you are not sure that with how much force you should shoot to throw the paper ball into the dustbin , so you randomly guessed some degree,
lets say 30% of your force and you make an attempt but you fell short. So you reattempt the shot making some modifications in your applied force based on estimation of how short the ball fell of the dustbin.
Now lets suppose you increase your force to 60% and you again throw a paper ball. But what? This time the ball just fell ahead of the dustbin. Looks like you overcompensated for the last time.
Now for your final attempt you are very careful and confident, you just need to reduce your throw force slightly. This time the adjusted force is 50% and BINGO! you did it!
Now you just got to hope that at least one of your friend fails to throw even a single ball into the dustbin and you will be safe :p.
This is more or less precisely what we do in findig gradient descent.
In the above example , first we initialized our force with 30% , This is **Random Initialisation** in Gradient Descent .
Then in second attempt we try to increase the force based on our analysis from the previous throw, similarly in Gradient Descent we generate **Predictions**.
We estimated how far the ball falls from dustbin, just the same way in Gradient Descent we calculate **Cost/Error** with respect to the actual value(the exact amount of force required to basket the ball in this case).
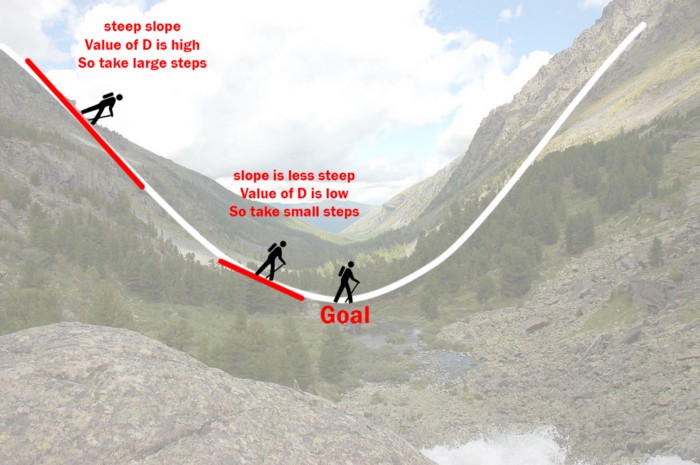
Then we adjust our force by updating it, similarly we update the parameters used in Gradient Descent i.e. **slope** and **intercept** in the Linear Regression Line.
We keep reattempting until we start scoring, and in Gradient Descent we keep making predictions iteratively until the cost function is minimum and ultimately we get the accurate results .
- Random Initialisation
- Generating Predictions
- Calculating Cost
- Updating Parameters