Update 8 September 2016: Current version of libPQP is deprecated due to a newly published attack. Possible mitigations:
- Forward-secrecy method where the secret key and corresponding public key gets updated over short intervals.
- Automatically reject any message which is decoded with higher error rate than some constant t, where t implies a negligable decoding error.
This is a simplistic prototype of a post-quantum cryptography library in Python. PQP stands for Post-Quantum PGP. The library is not production ready and should not be used in a real-life context, but works fine for testing purposes. The plan is, once the code has been audited, to translate it to Javascript and create a webapp.
In this prototype, the focus has mainly been on making the QC-MDPC part efficient and not the actual protocol. Hence, you may find vulnerabilities in the current implementation of the protocol. Also, the primitives used in the code are not the ones mentioned below. This prototype uses:
- AES-256(m, k, iv) as symmetric cipher,
- SHA-256(token + salt) as PBKDF2,
- A truncated SHA-512(token + salt) for iv.
The final product will use Salsa-20 as symmetric-cipher primitive and Poly1305 for authentication purposes. Moreover, PBKDF2 or similar will be used for symmetric-key generation.
Speed-ups in the decoding use the fast fourier transform (FFT) to achieve O(n log n) complexity in modular polynomial multiplications, instead of O(n²). Because the FFT implementation in Numpy is restricted to certain lengths (multiples of powers of 2), we use pyfftw which is a wrapper for FFTW3. FFTW3 implements Winograd's FFT algoritm and supports prime-length blocks. See below for known vulnerabilities.
Below are given the proposed parameters for rate R = 1/2.
| Public-key size | Private-key size | Rate | Error weight | Bit security |
|---|---|---|---|---|
| 4801 | 9602 | 1/2 | 84 | 80 |
| 9857 | 19714 | 1/2 | 134 | 128 |
| 32771 | 65542 | 1/2 | 264 | 256 |
Since the encrypted token is a codeword of length 9602 (for 80-bit security), we add approximately 1200 bytes of data to the ciphertext. Apart from this, a 32-byte MAC is included. This inflates a (padded) message of size M to size 1232 + M. For higher security levels, the inflation will be larger — but still constant. In the DER format, the inflation is about 35 %.
Today, most security assertions depend on primitives based on number theory. In principle, all of these primitives stand and fall on the problem of factoring integers. In the 1980's, a theoretical model of a computer that exploits certain quantum mechanical effects to achieve better complexity in certain classes of problems (BQP) was proposed. It so happens that the problem of factoring integers is contained in this class. Such a computer, called a quantum computer, can factor any integer N in time polynomial to the number of bits in N. This poses an actual problem for the security industry because RSA, ECC and DH, to name a few, can be broken efficiently. In turn, such a break causes the whole security architecture, upon which the secure internet is built, to collapse. Even symmetric primitives, such as AES, are subject to quantum attacks. However, the impact is much less severe; the speed-up in attacks is only a square-root factor.
To remedy the problem of quantum attacks, post-quantum cryptography was proposed. There has been many candidates, often based on so-called NP-complete problems. One such candidate is McEliece public-key cryptosystem, which is based on a hard problem called random linear decoding. Most of the linear-decoding problems are hard, but we should point out that some linear codes with special properties are very easy to decode. McEliece PKC extends this idea by defining such an easily decodable linear code, which becomes the private key. Then, a scrambled (random-looking) version of the linear code is used as public key. This faces the holder of the private key with an easy problem, but the attacker faces a hard problem.
1. Generate a linear code with generator matrix G (usually a Goppa code).
2. Compute G' = S × G × P, where S is an invertible matrix and P a permutation matrix.
3. Return keypair G, G'
Suppose Bob wants to send Alice a message m. To encrypt, he does the following:
1. Retrieves Alice's public key G'.
2. Compute ciphertext c = m × G' + e and send it to Alice
Note that these operations require basically no work at all, so encryption is very fast. Now Alice receives the ciphertext c.
1. Alice obtains c. Knowing S, G and P, she computes u = c × inv(P) = m × (S × G) = (m × S) × G + e × inv(P).
2. Using the generator matrix G (which defined an efficiently decodable code), she can decode m × S.
3. Having c' = m × S, the message is formed by removing the S, i.e., c' × inv(S) = m × S × inv(S) = m.
The QC-MDPC McEliece is a bit different, but the principle is the same. Instead of using matrices, it operates on polynomials (or, equivalently, circular matrices). Here, the private key consists of two sparse polynomials H₀ and H₁, which can be used to perform efficient decoding. H₀ and H₁ form the private key. The public key is H₀ × inv(H₁), which is not sparse and (presumably) cannot be used for efficient decoding. Encryption and decryption is done is similar ways to the above.
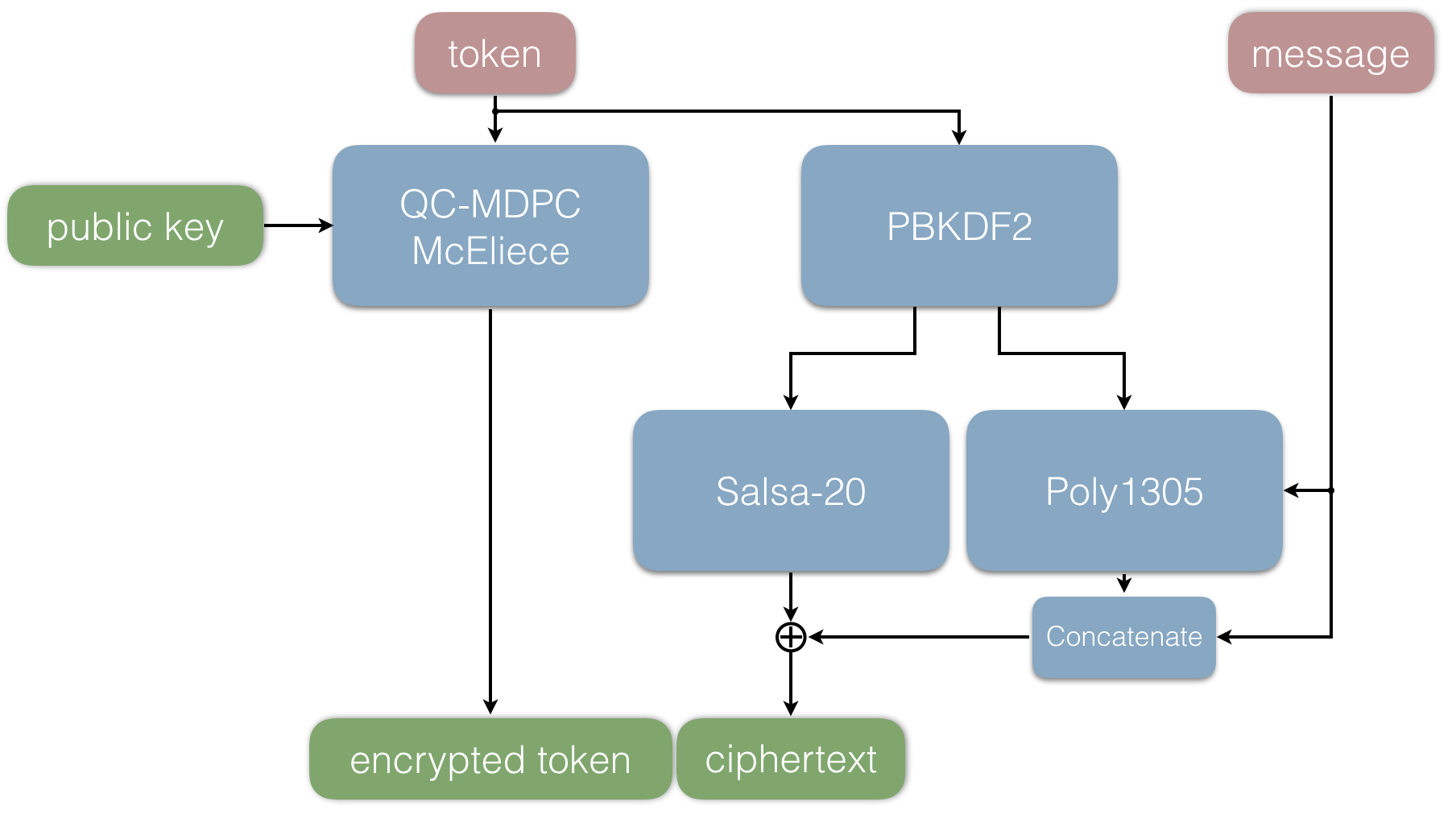
###The sender side
In this section, we will briefly describe the protocol. Much like a Fujisaki-Okamoto transform, it contains both an asymmetric part and a symmetric one. Consider the following scenario. Assume that Bob wants to send Alice a message. Denote Alice's keypair (pubkey, privkey). Bob takes the following steps:
1. Bob picks a random token T.
2. He then uses Alice's public key denoted pubkey and encrypts the token T using QC-MDPC McEliece.
3. The token T is used to generate the symmetric key k₁ and the MAC key k₂ (PBKDF2).
4. The error vector used in the second step is concatenated with the message and a MAC is generated using k₂.
4. The message and the MAC are then encrypted with the symmetric key k₁.
5. The ciphertext is the concatenation of the encrypted token and encrypted message + MAC.
The ciphertext can now be distributed to Alice, using arbitrary means of communication. Below is a graphical interpretation of the above steps.
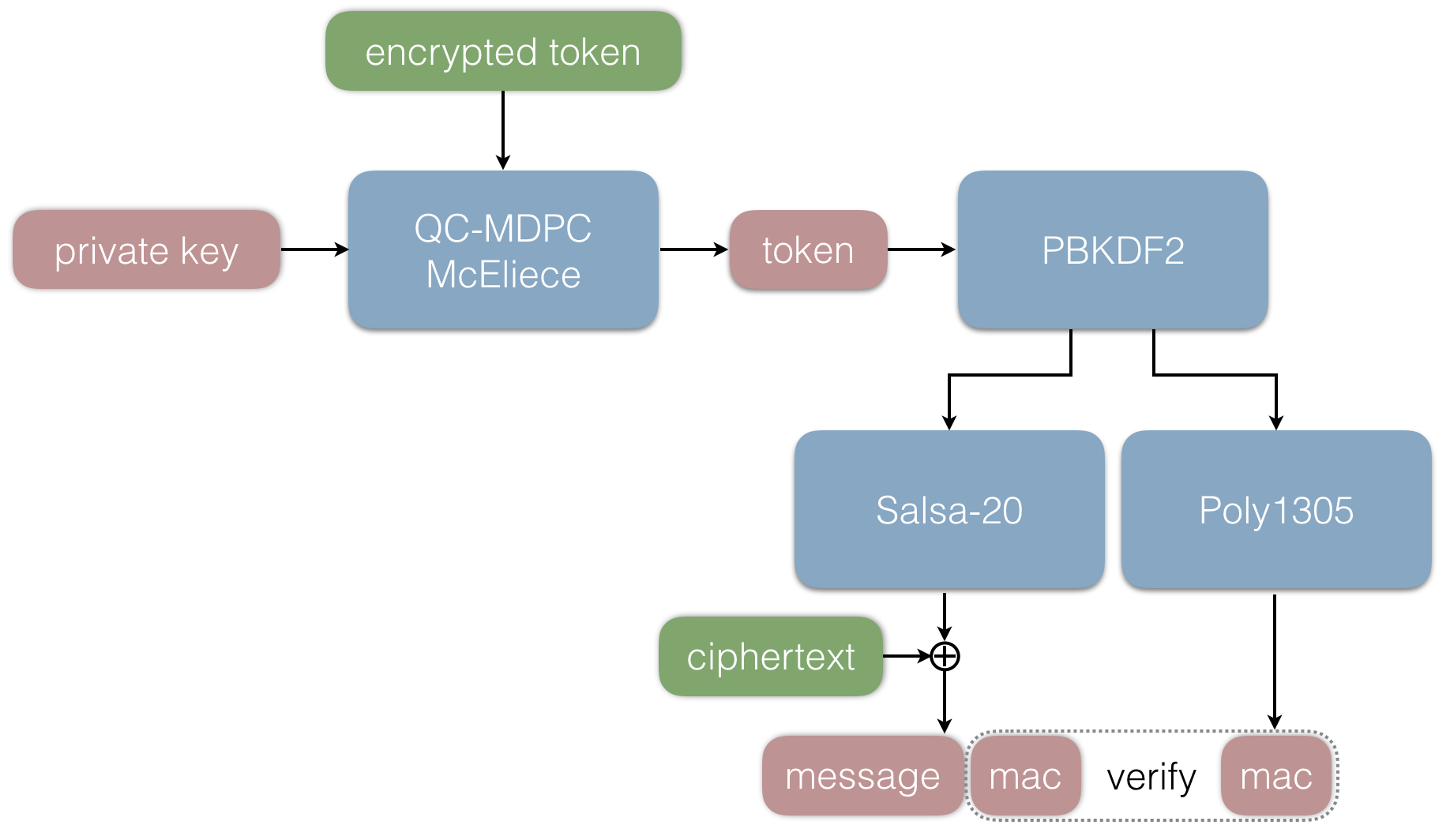
###The receiver end
Now Alice wants to decrypt the message sent by Bob. She performs the following steps in order to do so:
1. Alice decrypts the encrypted token T using her private key privkey. In the decryption, the error vector is determined.
2. Using the decrypted token T, she derives the same symmetric key k₁ as Bob and decrypts the message.
3. The message and the MAC are extracted.
4. The MAC of the message and error vector is verified using the key k₂ derived from the token.
5. If the verification returns True, Alice accepts the message. Otherwise she rejects it.
This completes the outline of the protocol. Below is a graphical interpretation of the above steps.
##Key format
The keys are encoded in Base64 and ASN.1, just like the normal ascii-armored keys used in public-key cryptography. The public-key structures contains only the generator polynomial G.
class ASN1PublicKey(pyasn1.type.univ.Sequence):
componentType = namedtype.NamedTypes(
namedtype.NamedType('G', pyasn1.type.univ.BitString())
)
A typical (encoded) public key has the following appearance:
-----BEGIN PQP PUBLIC KEY-----
MIICXgOCAloHMFAZsKjyqD4MKBPFkLCdUBAqC6rY4jdlOk/RQc4MiGfkUSw6hBh41eFa1XogH9MN
b49TPLQRZYBXygp7eGP1oUM4PqvvdwwOlUoTPNdWYeAiqEpOe4nP7sq+fir54nl84I/ArMdCsUyo
hgYtCVumC0XkYMlWW8tsW+RU94gQoQd7pLvgs98ah0gTNARRjW8/yALfGrB1pV7ZuLUScfNIFq8q
ZIZE8P80VK6kS0tcy+k4h9vHeB6QGPlPGB/jQ7mz8jDzw7v3m5QfnS1nlHvBSYWU/hADIIy13uh2
mEJmtIzDbWOZ7v4OJtDXrKgK9iMJ4OjCtntbmdAMSNwdMhNp2mH2O5a7b0MoELVILx6CTpjB64D2
toFwXwl867QEgBCk4imZHZxMgnLw9TxnM8g+5gQzfC5BCI6afaGS9lZXwbM+ssZN2DbRZIeVS7rI
12nul2rqquMC0buMM0Yt6ebD3bMRTeuUY3KLmEkUVjn3fTg7YUm82UuyGmG3cKqB0AZb24yswXl7
z3bOrMTMrggQXw0KPR3AoPh49+PG9pt9ySRp/9KZ8k+apXBtvxCOIx3J+6WYeB9zGTnu841jl+WD
LTBW5ePqglxGjown9lZlmw2Rgpsl7o6wSG5lb/d+B6hTw8w6KIowsQywEyDuF45B7U6W5EE8kgS1
9S01PKqkpYd9YV7oJzpYLFuS6dDW71WavV9DdW29uNOn5OlBAk79SbAjsliSojSVv5ZrYMPp16Sp
0YOkRoH/WeLL+xBwJtqMNRii34nH/B45ibEibCbFpO4rEDUs01aYAA==
-----END PQP PUBLIC KEY-----
The private key contains the two secret-key polynomials H₀ and H₁. Because inversion takes quite a while to perform, the inverse of H₁ is also contained in the private-key structure. This is not necessary, since inv(H₁) is only used when deriving the public key.
class ASN1PrivateKey(pyasn1.type.univ.Sequence):
componentType = namedtype.NamedTypes(
namedtype.NamedType('H0', pyasn1.type.univ.BitString()),
namedtype.NamedType('H1', pyasn1.type.univ.BitString()),
namedtype.NamedType('H1inv', pyasn1.type.univ.BitString()),
)
Below is a typical private key given. As we can see, the elements H₀ and H₁ are very sparse. These polynomials could be encoded more efficiently, but we don't care too much about private-key size and is therefore left as is.
-----BEGIN PQP PRIVATE KEY-----
MIIHGgOCAloHAAAAAAAAAAQAAAAAAAAAAAAAAAAAAAAAAIAAAAAAAAAAAAAAAAAAAAAAAEAACAAA
AAAAAAAAAAAAAAQAAQAAAAAQAIAAAAAAAIAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAEAAAAAA
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
AAAAAAAAAAEAAAABAAAAAAAAAAAAAAEAAAAAAAABAAAAAAAAAAAABAAAAAAAAAAAAAAAAAAAAAAA
AAAAAAAAAAAAAAAAAAEAAEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAAAAAAAAAAAAAAAAAAAAAI
AAAAAAAAAAAAAAIAQAAAAAAAAAAAAAAAAAAAAAACAAAAAAAAAAAAAAAAAAAAAAAAAACAAAAAAAAA
AAAAAAAAAAAAAAAAAAAAAAABAAAAAAgAAQAAAABAAQAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAABA
AAAAAAAAAAAAAAAAAAACAAAAAAAAAAAAAAIACAAAAAAAAQAAAAAAAAAAAAAEAAAAAAAAACBAAAAA
AAAIACAAAAAAAAAAAAAAAABAAAAAAAAAAAAAAAAIAAAAAAAAAAAAAAAAAAAAAAAAgAAAAAAAAAAA
AAAAAAAACAAAAAAAAAAAAABAAAAAAAAAAgAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
AAAAAAAAAAAAAAAAAAAAAAAAAAAAIAAAAAAAAAAAAAAAAAAAAAAAAAOCAloHAAAAAAAAAAAABAAA
AAAAAAAAAQAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAQAAAAAAAAAAAAAAAAAAAAA
AAAAAAAAAAAgAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAgAAAABAAAAAAAAAAAAAAAAAAAAAAAAAA
AAAAIAAABAAAAAAAAAAAAAAAAAAAAAAAAAAgAAAAAAAAAAAAAAAIAAAAAAAAAAAAAAAAAABAAAAA
AAAAAAAAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAAAAAAAAAAAAAAQAAAAAAAQAAQgAAAAAAAAAAAA
AAgAAAAAAAAAAAAAAAAAAAAgAAAAAAAAAAAAgAAAAAAAAAAAAQAAAAAAAAAAAAAAAAAAAAAAAAAA
AAAAAAIAACAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAAAAAAAAAAAEAAAAAAAAAIAAAAAAAAAAA
AAAAAAAAAAAAAABAAAAAAAAAAAAAIAAAAABAAAAEAAAAAAgAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
AAAAAAAAAAAAAAAAAAAAAAAAAAAACAAAAAAAAAAABAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAEAAAAAAAEAAAAAAAIAAAAAAAEIAAEAAAAAAAAAAAAAAAA
AAAAAAAAAAAAAAAAAgAAAAAAAAAAAAABAAAABIAAAAAAAAAAQAAAAABAAAAAAAAAAAAAAAAQAAAA
AAAAAAAAAAAAAAAAAAAAAAAAAAOCAloHPmFZHOhZjZWveH7OKtPghL5WWVE2/JctV4GYBnliCjZ3
qyR/x741dDTCa8O1vAq0HaezSJL0H4rehid7KaLkQ4OTwwbwk22nLuQIi6ShXYCL1Tlbd4POVxGa
RSQn/zQjIGGZ009mNraWv+MyyNDE5WMfl0VqcjYhYacAgf7NXc3tUHKXCYHxzf9P3IbQvwFUOTUC
A2x4kI0yGaBs2Y/wtJkSkvsayxlSqNIu8Ob5I3aFqndhVLvlKgsG00iLzLLFRqSYTCeYnM1pV9Mv
ZgRM5Esdv/O9XNcdKMTGRcV357jqdN+MvJhxitmyvIUpez9kh6+yt+PRtXUzWyVs2x6mf/OScL5f
HznX3uePZl02G4ug/ro3eh/T8wjC9j6CtX3WgnqYKo2n68+fvt6EaEL7lZoMnVgTHHwx1HuQl0pl
OEj2WnwHcAuYleOrNtKMtDpji0e90cXGURujMymS58ZNCyHdX7qCm7MlfmS0l6YZ/my8vRGxPG83
qksVuNMvB9dKEzpTzWLIlygMDvjzn9GN/071iRp9lNaPliZD4x8Dt6d4QS3pOUCw/oPWNUCHJUOW
dBUO5ziqZ+4Xt68Gce4FB7/jb2ejsAPstzzrpLKvvpmo4FL+ibx17TnbEhyNlJ+N94CQ+TSELzqi
QHzg3PtOxZOPxbT5RQSkSQjVIaUH6/k2TC20iorr6gsH8Oogz24to+E41aZT0NBzxrZvuI/yuB0N
XAT/wwcIth3UVQoT5Y0lnXVUKnBF89PHUayLawWgxPiDx5EHhjsWqyB/G/VB2ZhFx6qnfE+qAA==
-----END PQP PRIVATE KEY-----
The messages are structured in a similar way. The encrypted token (C₀, C₁) is stored in two separate Bitstrings and the symmetric ciphertext are stored as an OctetString.
class ASN1Ciphertext(pyasn1.type.univ.Sequence):
componentType = namedtype.NamedTypes(
namedtype.NamedType('C0', pyasn1.type.univ.BitString()),
namedtype.NamedType('C1', pyasn1.type.univ.BitString()),
namedtype.NamedType('Sym', pyasn1.type.univ.OctetString()),
)
We encrypted the message
this is a really secret message that is padded with some random.
and put it into the ASN.1 format. Below is the ciphertext.
-----BEGIN PQP MESSAGE-----
MIIFHgOCAloHOjScypeSXUoEDjfC+E3GGYbQ7t2QQ8Z7LtfPG0SOjySJWuWszQ2F593vDr41hQFV
dpdgSElPrWMiAxhqZ11fj3DVXCTZtu5DwXBijtVKg55xs/fu9rh6RvywIKdRLTpxJfVrN1oGA7rs
oaPvToZPOziXdymst4Z3dDc5vcyPORQXZz3KmhLKowFtrHpPx7HMVdi2iXy2ohKGBafdtpZsOHek
K8JgtLQhlC/cQbXkd5uWniWn/qSei6zKVpOCO7PvqLadJCJI2rufue2Lie+AmQGVmn4DK8X5c+I8
4BEVTY6PtZ819vyQmOARO0qSNr/6qiV0u1X7VFLGw+tvYjrDAvmiWTujQ7uY9Qs2ef0idk+4GmnK
JqImt+ExnKedH8O5NWxZewHnFoU23gL3Qz1eODnHYVOQxfvUtQnuZMRuHgbrc+av22pi0C+aj0qR
JW4vcqNEazeD6usot28Uo7tpnqs1kAssHqGAQ0rAtDkdogpq5ntQidb4yheaj1orgcT7/VyugKbH
Di0NeyoG/wo9vi5aCDlw0e0KPHKat0wvR21FYSCqtd9Gmc6/McDGYTwaJLZ4NK53ETnaJh46X9jd
OZTL9eSOKrbElZjlIMWAVXZgU465lGoENZVDNCV9AgzMsku0o/VV2Djh8Hw/Ggx0sAlpbjc+AuD4
xEa3gETXKdmsq/PjATe9c9+5I0oO17rIjwlc+Wc5w4NGJuBrm0MNtkzEzVyteXsn00njiNdrxRks
gaUcpkwleLawIZh7gs1X3SRI7+VWvBy/8t/n9LxERC6/rkyJbC5kAAOCAloHHtIcwG1S+00bmFb8
C5uYTW47XcP/eP+U9tjVswkgj/wu/RjmqGuGISw8ys2vmi79429gvXQRwLiH3NaPP8WpF2vo52H0
gVVLYqmWtMG5gLKwxEFr22OGe/nNnj49Rk57nhpp+i2EUFmWbigrAcClcVxeB5BYlxlM08VeTJeU
OeRlRJaaBFk2GRETnAPST3RsyLwz9dW0njZkeQGPG+rIXp5J/exUsn+WSq/omYivTujCHACZ1Fxt
Bx0fD1PXxGVhGrXodENAn1R0AeG/E3g/M++vfTaG2nba+kkO/2lrMKfWTOp/cvpyzHk9gNDc5EXM
A1MqUI7z9/defLHVIwo6u5xHjAx3c+qZ2YwEJmaar7c70NUfjvOPhGQsH9Pcs18BVv7WyswDT8/C
wtKCv9PY5BVUBvp2wKCfmhuPdNYxzA3F/zPL+ryFUjMrdBnWmYaI1hQXdeUY0DzM6mWPEfLgWnIG
PKX6CmsbJNQs3+GC31ps7GkCZkYdBoSlBf9faFnLCzsx2AMKOx32ZKVyU4v0WzvRNF1VQyq6NQyh
Ap7phcIvq9DkBSdWe2pEpbctYbUqVLeZ5tpz0zCFWrdDHvvDSg4OA3J3QEvSA4V1fCzQY6QG9EGC
8mlXorT+aKlvJz6gWOZcurwrM307cYOx9yC0QACQPItWXXt8E6fpXjxgJs4mMwnWGoW7H51xziRH
m+VIP0qdHCvEzI2180qE0oEOfIh8MbLFWktovkjy94US6AGTxZ/GP2o8ALKvRfvB603X5m8PjBlj
JGPyik2nqjqIJXK95F9omr4FgARgSUda/5bzJK/tJUuixFOWWaimI+WtgJDsIV8velkaaVvxL8xz
K7PlOCNoMaZYC+z/GkenwwvNr0f+uGiPYShao0/Ie7NhC2C2tj61OENmc+OJ1zy1qLE1ApJOlVL3
KHde
-----END PQP MESSAGE-----
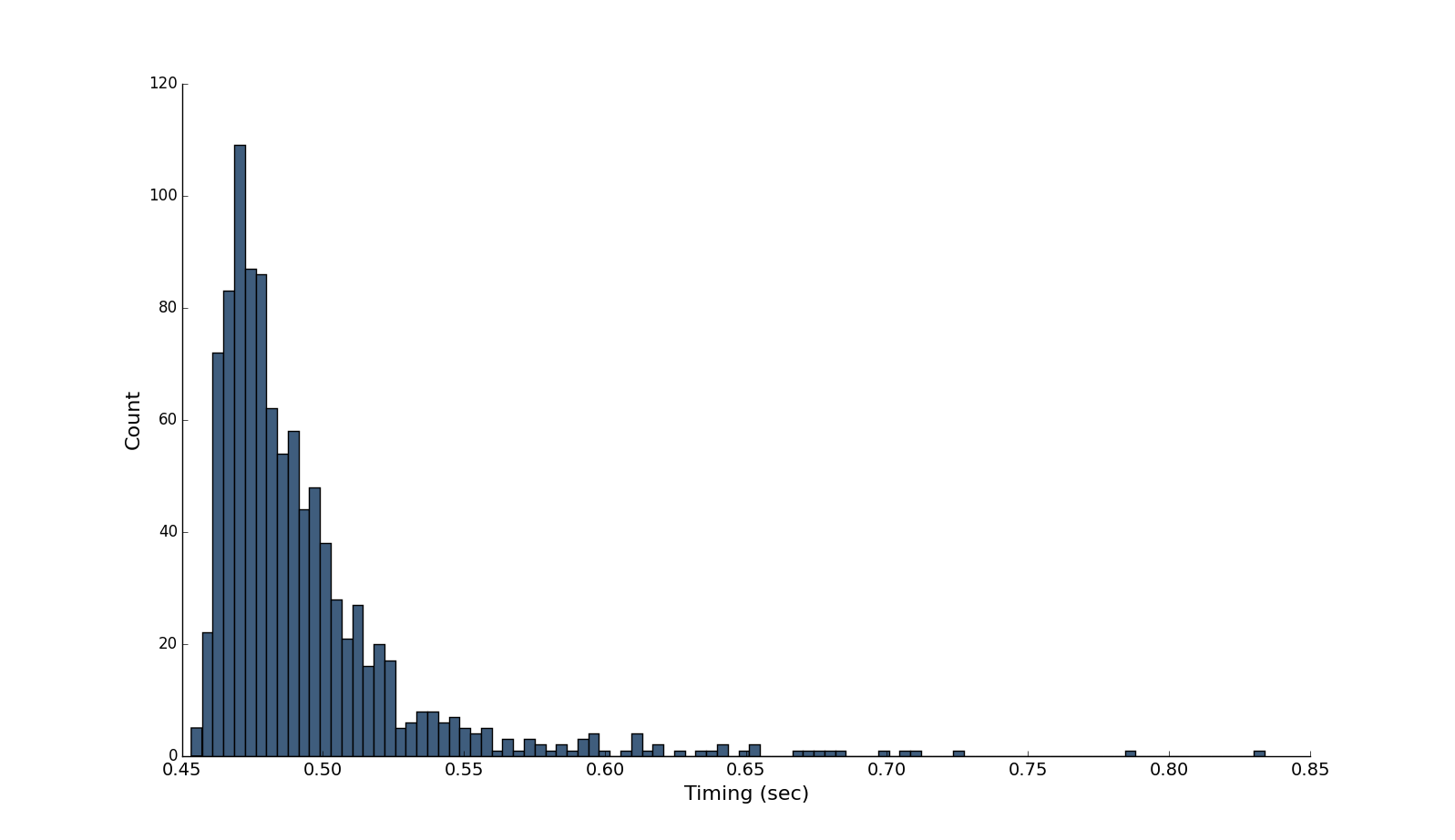
#Performance Below is a graph of timings of my computer (Macbook Pro 15" Retina 2 GHz Intel Core i7) running 1000 decryptions of a small plaintext (thus, isolating the asymmetric timing) using the same private key (σ = 0.0386, μ = 0.493):
Here is the output of encrypting and decrypting a 190 mb video file:
$ time ./pqp --encrypt libpqp.mov --pubkey pub --output libpqp.enc
Encrypting: libpqp.mov
real 0m11.331s
user 0m9.293s
sys 0m1.715s
$ time ./pqp --decrypt libpqp.enc --privkey priv --output libpqp2.mov
Decrypting: libpqp.enc
MAC verified.
real 0m11.422s
user 0m8.633s
sys 0m2.446s
$ ls -la libpqp*
-rw-r--r-- 1 carl staff 258900672 17 Jul 00:57 libpqp.enc
-rw-r--r--@ 1 carl staff 191652442 16 Jul 23:22 libpqp.mov
-rw-r--r--@ 1 carl staff 191652442 17 Jul 00:58 libpqp2.mov
$ md5 libpqp2.mov
MD5 (libpqp2.mov) = 88ebe9d8aa74ebba7c5de6faa048af46
$ md5 libpqp.mov
MD5 (libpqp.mov) = 88ebe9d8aa74ebba7c5de6faa048af46
#Command-line tool The library can be invoked by a supplied CLI tool (the pqp file). Padding is not included, so some kind of PKCS padding will be added.
To generate a keypair, run the following command:
pqp --gen [private-key file] [public-key file]
This creates two files in the same folder containing the two keys.
To encrypt a file, call pqp as follows:
pqp --encrypt [plaintext file] --pubkey [public-key file]
This writes an ASN.1 encoded ciphertext to stdout. Appending --output writes to file:
pqp --encrypt [plaintext file] --pubkey [public-key file] --outout [ciphertext file]
To decrypt, invoke the following command. To write to file, use the above methodology.
pqp --decrypt [ciphertext file] --privkey [private-key file]
#Installation
Below are the required steps to make libPQP run on Linux (tested on Ubuntu 16.04 Xenial):
git clone https://github.com/grocid/libPQP.git
sudo pip install numpy
sudo pip install pycrypto
sudo apt-get install libfftw3-dev
sudo pip install pyFFTW
sudo pip install pyasn1
#Possible vulnerabilities
##Decryption oracle The protocol can be designed using normal McEliece or Niederreiter. In case of McEliece, the error vector should be part of the authentication (for instance, generate MAC using a concatenation of message and error vector). Such a measure will mitigate the usual decryption oracle attack, described below.
1. Intercept an encrypted message.
2. Pick a random bit of the ciphertext.
3. Flip it. If decryption fails, this was not an error position.
4. Repeat until all error positions have been unraveled.
Obviously, there is an implicit assumption that the receiver will either reject any error larger than T or the decoder will fail (which rarely is the case).
If the protocol instead is designed using the Niederreiter model, the error vector will be/encode the token. In this case, there is no need to authenticate the error vector. Since any flipped bit in the ciphertext will cause the receiver to decode a different token, it will break the decryption oracle.
##Timing attacks
This is a slight variation of the above. Instead of observing decryption errors, we measure the timing. There has been some effort in making decoding run in constant time. See this paper.
The decoding we use is probabilistic and susceptible to timing attacks. Below is an image with the timing attack implemented running 15 decryptions for each bit flipped.
However, in the PGP-like setting we do not worry too much about this.
##Distinguishing attacks
The simplest imaginable distinguisher will detect a constant-error encryption with probability 1.
1. Pick a ciphertext block with block weight l and error weight w.
2. Sum all symbols mod 2 and check if it equals (l + w) mod 2.
The theory is described in more detail here. There is an easy counter-measure; we can thwart this attack completely by picking the error weight odd with probability 1/2:
1. Flip a balanced coin.
2. If the coin shows tails, pick a position at random and flip it.
This attack is contained in distinguisher.py.
##Squaring/subcode attacks
Squaring attacks exploit that (the now deprecated) p = 4800 = 2⁶ × 75. By squaring the polynomial, the vector space decreases in size by a factor 2 (which can be done six times). It may also lead to collisions in the error vector, causing a decrease in error weight. This allows an attacker to go quite far below 80-bit security. See this paper.
This attack can be mitigated by picking a prime block length p. In the example above, p = 4801.
#Academic papers MDPC-McEliece: New McEliece Variants from Moderate Density Parity-Check Codes
Lightweight Code-based Cryptography: QC-MDPC McEliece Encryption on Reconfigurable Devices
Squaring attacks on McEliece public-key cryptosystems using quasi-cyclic codes of even dimension
#Acknowledgements Miroslav Kratochvil (creator of codecrypt) for pointing out a weakness in the protocol.