-
Notifications
You must be signed in to change notification settings - Fork 61
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
[Research idea] Stopping rules #178
Comments
|
Found this gem of a stopping rule in MSPPy (#208) and it's somewhat related |
|
Reading the ideas in MSPPY that you mention, and since I already tweaked the Statistical stopping rule, several things come to mind:
|
|
Hi, is that possible to add a deterministic upper bound? The intuition is that, since the lower bound is the outer approximation of the value function, the upper bound can be calculated by the inner approximation (naturally). This paper discussed this approach. https://doi.org/10.1137/19M1258876 |
I have no plans to do so. Note that the formulation SDDP.jl uses is non-standard in the literature. We can handle integer variables, non-convex subproblems, and we have objective and belief state variables. A much more problematic issue is that the inner approximation requires significantly more computational effort. So it doesn't really make sense to use it. I think the stopping rule outlined above more closely matches what people expect. p.s. I see you have https://github.com/zidanessf/RDDP.jl. I opened a couple of issues. Happy to chat about anything in more detail |
|
I think the inner approximation in this form has little computational effort. |
|
A few points on the computational effort:
The last point is pretty subtle: it often happens that the gap can be very small, but if you look at simulations of the policy the performance is great for 98% of the simulation runs, and terrible in the 2% (i.e., you haven't added cuts along those trajectories). Because those bad trajectories only account for 2% of the total, and they might not be very terrible, their total contribution to the objective function may be very small. Thus, you can have a small gap even with visibly poor trajectories! The stopping rule about attempts to quantify this: you want to stop when things "look" good, regardless of the exact quantitative performance of the policy.
O boy yes, the Lagrangian cuts are tricky to get right. I've had a few goes with little progress. Maybe I need to revisit the upper bounds. I know @frapac did the original experiments here: https://github.com/frapac/DualSDDP.jl |
|
@zidanessf: I just spoke to some folks how are hoping to have a postdoc work on SDDP.jl. They mentioned the same upper bound :) I now understand how it works much better. If they get the funding, we should have more to report on this front. They also had some good ideas for how to use the upper bound in sampling. |


Without an upper bound, the question of when to terminate SDDP-type algorithms is an open question in the literature. Thus, we need some heuristic for preemptively terminating the algorithm when the solution is ''good enough.'' We call these heuristics stopping rules. Choosing an appropriate stopping rule depends on the motivation for solving the multistage stochastic optimization problem. In our view, there are three possible motivations:
Currently, there are two main stopping rules in the literature:
Both of these stopping rules target the first use case. (Although the statistical stopping rule implicitly targets the 2nd and 3rd motivations though the simulation.)
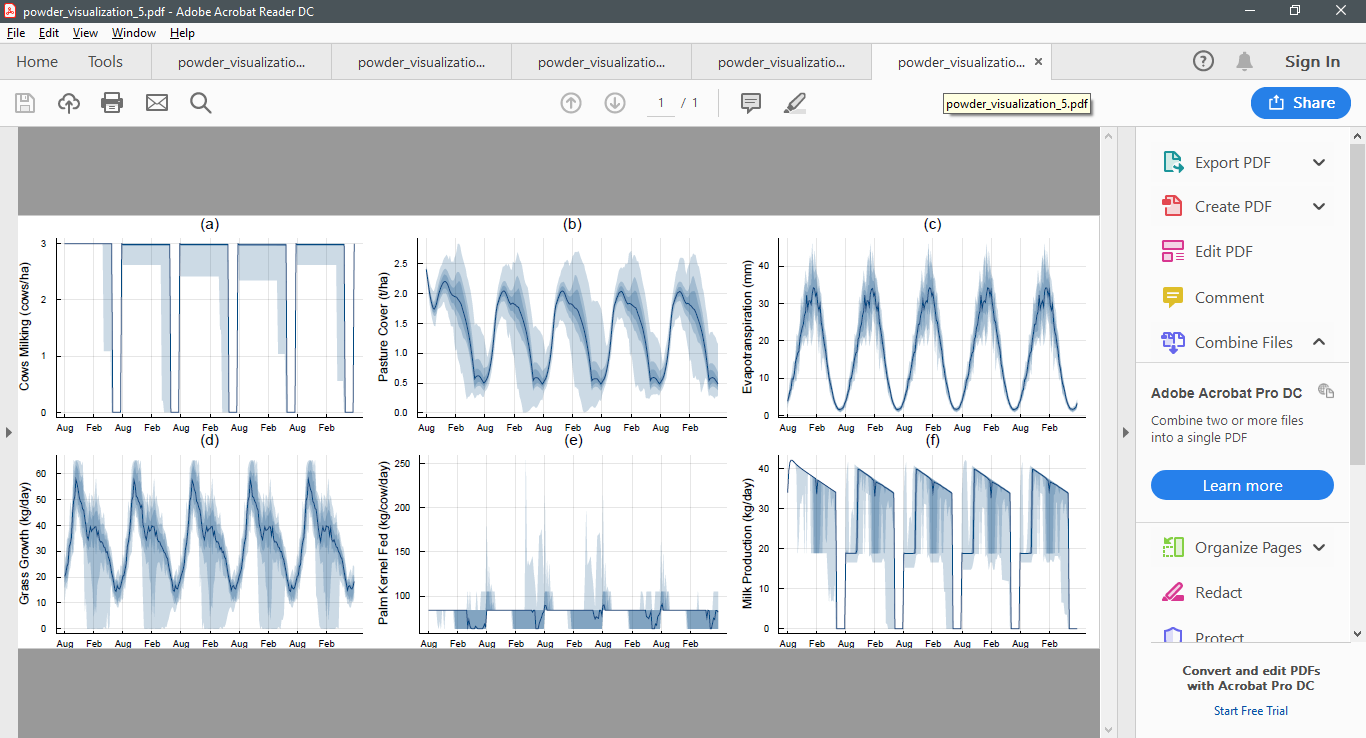
I propose a different stopping rule based on the "stability" of the primal (or dual) policy.
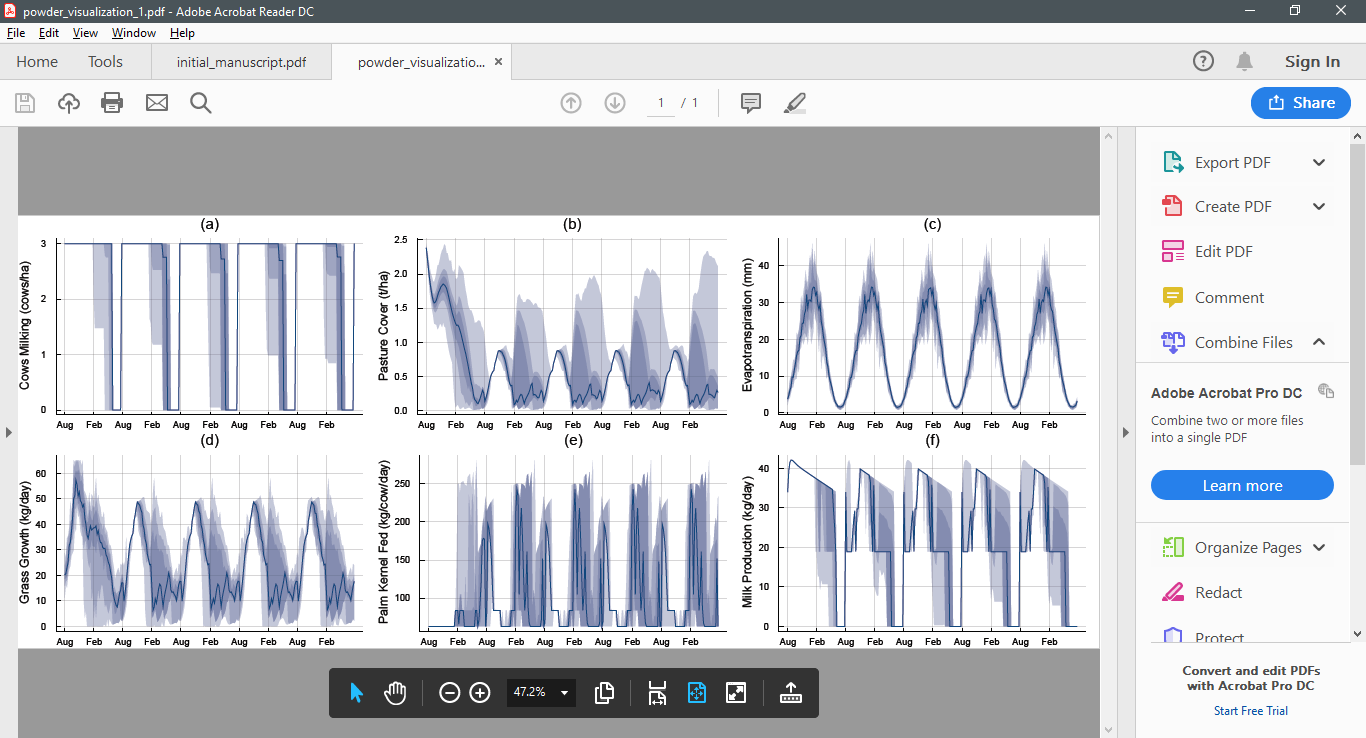
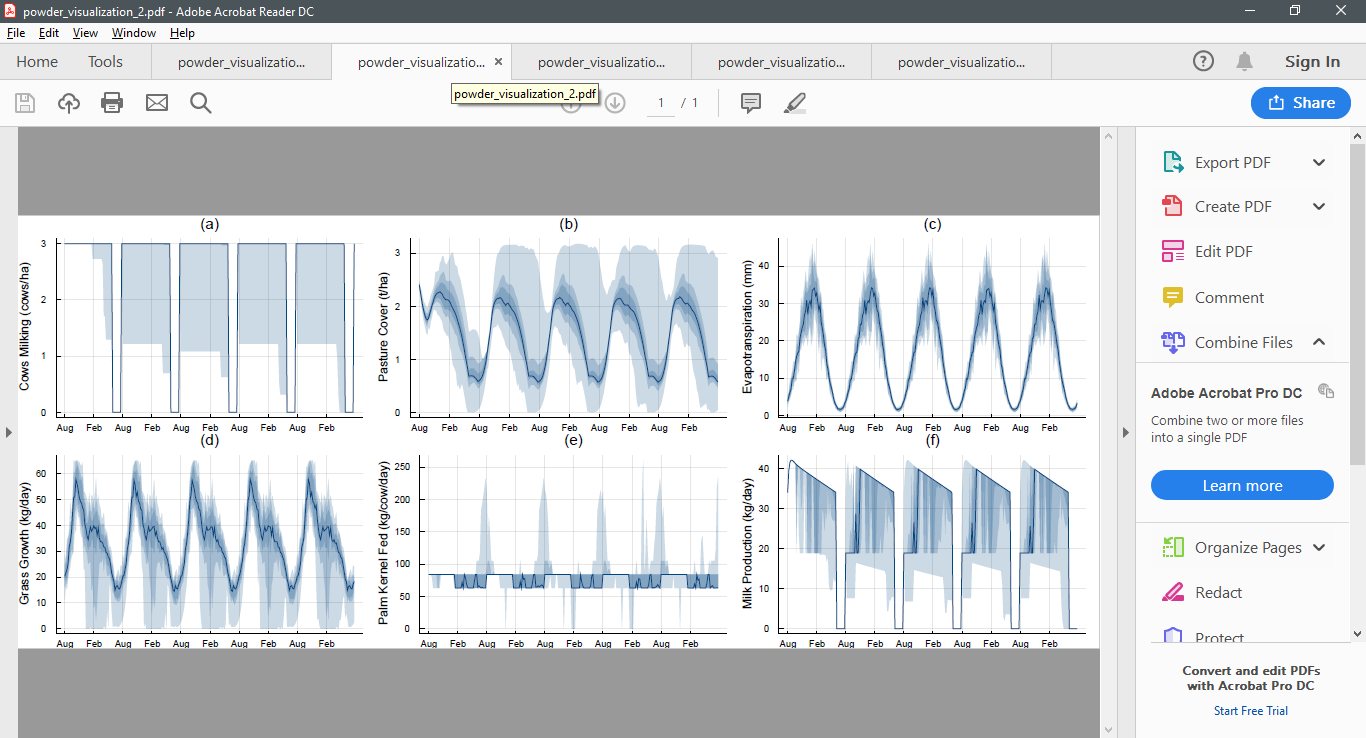
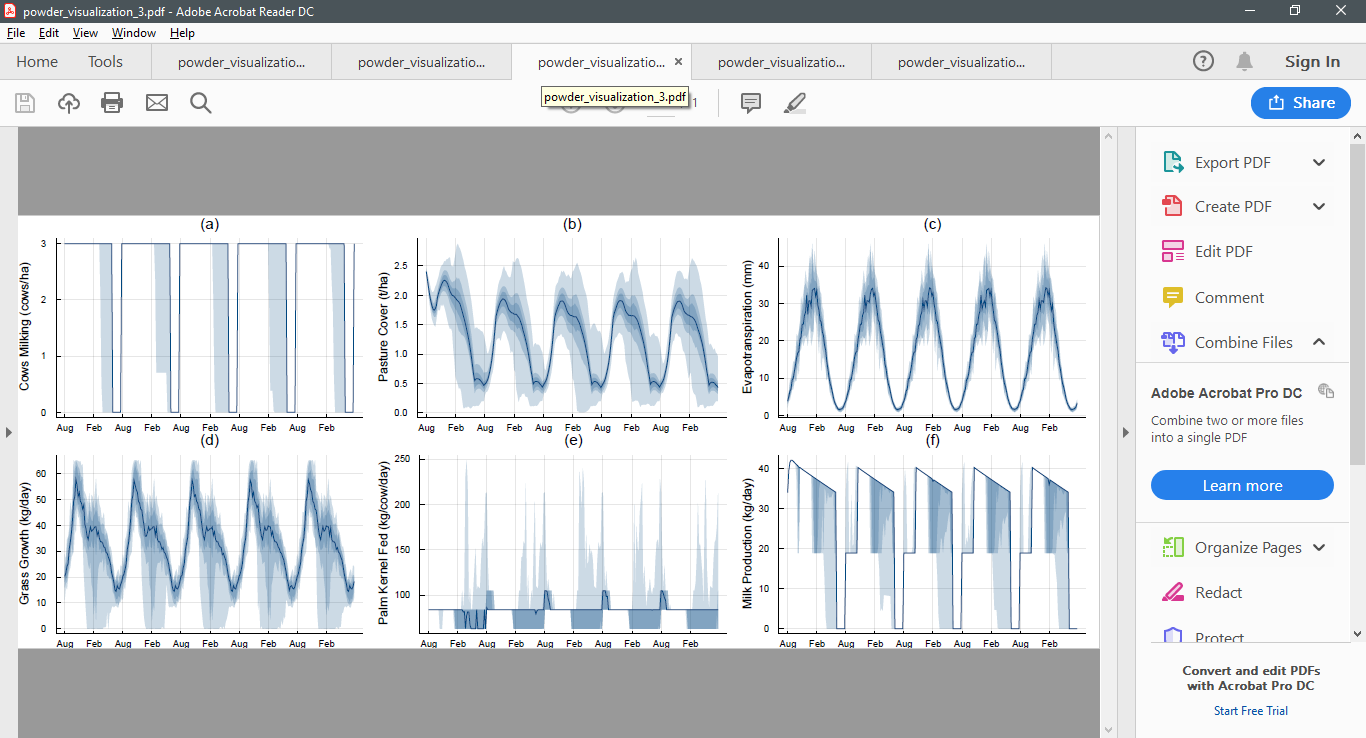
To test for convergence, periodically perform a Monte Carlo simulation of the policy. Then, for select primal or dual variables of interest, compute at each stage some quantiles (e.g. the 10, 25, 50, 75, and 90'th) of the distribution of the value of those variables.
Then, using some appropriate norm, compare those quantiles to the values calculated at the previous test for convergence. Terminate once this distance stabilizes.
As an example, here are five simulations from the infinite horizon POWDER model conducted after 100, 200, 300, 400, and 500 iterations. Notice how the policy begins to stabilise.
After 100 iterations
After 200 iterations
After 300 iterations
After 400 iterations
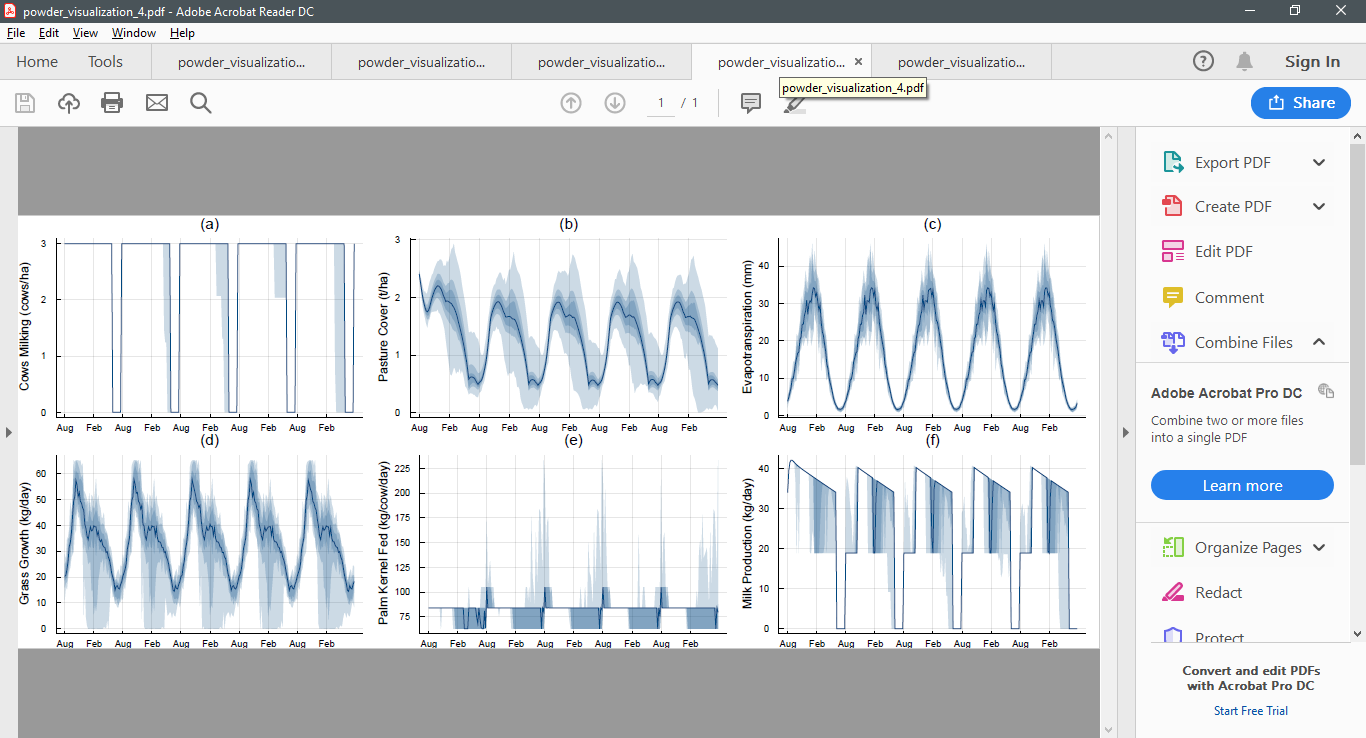
After 500 iterations
Existing literature
cc @dukduque potential paper?This has been discussed before by Alexandre Street and co:
The text was updated successfully, but these errors were encountered: