Compressed NNUE weights size

[ddobbelaere]

I just did a small experiment (namely "xz -z -9e" (max. xz compression)) on some NNUE nets of https://tests.stockfishchess.org/nns
Here are the resulting file sizes in bytes:

Sergiovieri run and derivatives (leading to all recent master nets):

9776088 nn-82215d0fd0df.nnue.xz (sergiovieri) <-- master^10
9721312 nn-112bb1c8cdb5.nnue.xz (sergiovieri) <-- master^11
9642504 nn-62ef826d1a6d.nnue.xz (SFisGOD)     <-- master
9642504 nn-c3ca321c51c9.nnue.xz (SFisGOD)     <-- master^1
9642504 nn-cb26f10b1fd9.nnue.xz (Fisherman)   <-- master^2
9642504 nn-2eb2e0707c2b.nnue.xz (SFisGOD)     <-- master^3
9642504 nn-eba324f53044.nnue.xz (vdv)         <-- master^4
9642504 nn-04cf2b4ed1da.nnue.xz (vdv)         <-- master^5
9642504 nn-baeb9ef2d183.nnue.xz (SFisGOD)     <-- master^6
9642504 nn-04a843f8932e.nnue.xz (vdv)         <-- master^7
9642504 nn-03744f8d56d8.nnue.xz (sergiovieri) <-- master^8
9642500 nn-6554800d4b0c.nnue.xz (Fisherman)
9639372 nn-308d71810dff.nnue.xz (sergiovieri) <-- master^9

Other runs:

8772772 nn-30f6ddc579c2.nnue.xz (noobpwnftw)
8771688 nn-91fec6f6756a.nnue.xz (noobpwnftw)
8613628 nn-ddbf15bd12bd.nnue.xz (vdv)
8589724 nn-64fc1e0029b5.nnue.xz (noobpwnftw)
8589528 nn-31c47f9dbd91.nnue.xz (noobpwnftw)
7680524 nn-be652a0c885a.nnue.xz (vdv)
6928364 nn-01de8d92ba3e.nnue.xz (glinscott)
6775392 nn-11c4729f1ece.nnue.xz (vdv)
5923328 nn-26b7fcdb21c6.nnue.xz (vdv)
2563132 nn-a20699671e55.nnue.xz (MiauiKatze)

It seems that the compressed weights of the successful run of @sergiovieri, along with its derivatives (mostly post-optimizations of final layer) are at least about 1MB bigger than all other independent runs.

If this size is a measure of entropy (information content), it seems these networks encode more knowledge. Maybe regularization is too strong for the other independent runs (this is just a bold hypothesis), dragging the weights more towards zero and forgetting previously learned knowledge more quickly?

[ddobbelaere]

Apparently the pytorch trainer doesn't explicitly use an L2 regularization term as part of the loss function (as opposed to AlphaZero/Leela Chess Zero), nor does the Nodchip trainer.

In the pytorch trainer, an optimizer called Ranger is used that does all the grad-based training.

One thing I read from the docs is: "Best training results - use a 75% flat lr, then step down and run lower lr for 25%, or cosine descend last 25%."

It's not obvious to me that the latter part is supported by the current pytorch trainer, or am I mistaken (I see only a single flat LR)? It may be possible to work around it via checkpoints though (using the current codebase)...

@vondele Unless I am mistaken, I also don't see any experiments related to this in https://docs.google.com/document/d/1UJe9dT8YAz-Z5sGWD2IwFZHD1F0EL6zjNoeS0gaYpBE, maybe it's a worthful idea to try?

[vondele]

right now it is a flat LR. I think it could be worthwhile, but nobody wrote the code for it yet..

[ddobbelaere]

Hmm, ok. My limited experience from (following) Leela Chess Zero, where the LR is piecewise constant during training (typically factor 10 smaller at each so-called LR drop, if loss has converged), is that the final nets are typically hundreds of elo stronger than best nets at first LR region. After each LR drop (of which there are typically three), the loss function typically converges in exponential fashion to a lower plateau (on your loss curves I only see one such regime).

I have no experience with Ranger, but anyway they recommend a final "annealing" phase with (possibly gradual) lower LR, so this seems very promising to me.

As I mentioned earlier, running with a final lower LR on an already converged run loaded from a checkpoint might be a first step (without changing any code)?

[ddobbelaere]

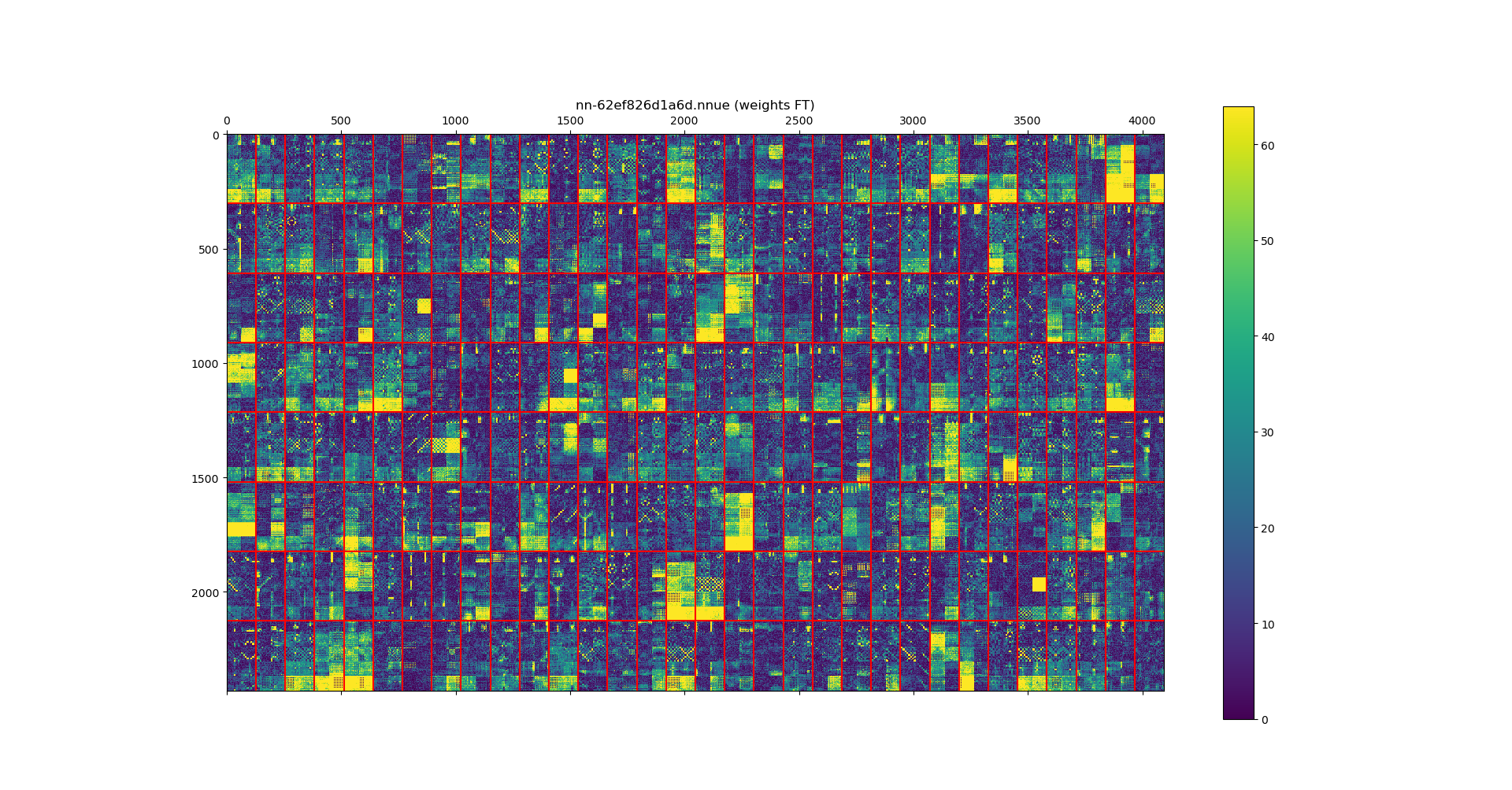
I just hacked together a script based on https://github.com/glinscott/nnue-pytorch/blob/master/serialize.py and https://hxim.github.io/Stockfish-Evaluation-Guide/ to investigate the weights of the input to feature transformer.

Let's load all the weights w and visualize min(64, abs(w)) for the current master net (nn-62ef826d1a6d.nnue) and the best vdv net tested on fishtest (nn-ddbf15bd12bd.nnue).

The results are surprising:

A red box of size 304x128 corresponds to all the weights connected to one feature (there are 256 boxes). Note that I, just like https://hxim.github.io/Stockfish-Evaluation-Guide/, drop the Shogi BONA thing and also pawns on first/last rank, i.e., 304 = 64*4 + 48.

Note that in the vdv net there are features that are as good as dead (not excited at all!).

I hope there is not a big issue with training, e.g. dying ReLU issue in final layers (see https://en.wikipedia.org/wiki/Rectifier_(neural_networks)#Potential_problems), which can be caused by absence of regularization (in combination with other factors, e.g. too high initial LR or bad initialization).

@vondele If you have any other (better?) nets to investigate, let me know.

[ddobbelaere]

Same exercise for best noob net on fishtest (nn-64fc1e0029b5.nnue). No visual indication related to dead features here at first glance.
@noobpwnftw Did you use Nodchip trainer for this net or pytorch trainer?

Apart from the visual observation of dead features on the vdv net, it is interesting to investigate mean(abs(w)):

net	fishtest elo	mean(abs(w))
nn-62ef826d1a6d.nnue (master)	N/A	20.56
nn-ddbf15bd12bd.nnue (vdv)	-29.36 +-3.1 (95%)	16.26
nn-64fc1e0029b5.nnue (noob)	-33.04 +-3.5 (95%)	11.37

All these observations give us an intuitive explanation why the entropy/compressed file size of the master net is highest.

[ddobbelaere]

Now that I think of it, a final "normalization" before exporting to quantized nnue format might be possible (and highly desirable!) as follows:

Ensure that dynamic range of weights for each input feature is high enough by scaling biases/weights in layers that follow, such that the (normalized) non-quantized net remains equivalent to the initial net.

EDIT: I forgot that we use clipped ReLUs, which makes this idea impossible (or only possible within some (probably unacceptable) limits).

[vondele]

@ddobbelaere interesting analysis. It indeed looks like this could be an issue with the training.

noob is using the nodchip trainer.

[vondele]

BTW, do you have a link to your script? Even better, what about a PR to the pytorch trainer.

[Sopel97]

I find the results kinda weird. We observed dying relu problem with the nodchip trainer but it only happened with very high LR and after the first initial batch. The pytorch trainer uses a much lower LR (and requires much longer training to get a good net). They both use the same loss function, nodchip defaults to LR=1 which is fine, ranger has LR=1e-3 (unless it does something weird at the start?). So this is likely not cause by the learning rate.

[ddobbelaere]

The script can be found at https://gist.github.com/ddobbelaere/ad4e2645828b3fbd771249e37cfc2d0a. I've warned you it's hacky :). Unfortunately, I don't have the time at the moment to create a PR for pytorch trainer with a proper "visualizer".

[ddobbelaere]

@Sopel97 Yeah, I also don't know what the issue is to be honest (if there is any).

I just did a bit more research on the feature transformer layer. The clipped ReLUs of the "dead features" of the vdv net all have a small (negative) bias term:

I'm not sure if this is good or bad news. Probably the clipped ReLUs are not completely dead yet (some inputs might kick them back to life), but maybe still on the verge of dying?

Or maybe the combination of training and input data had no way to extract any more useful features back then? Or maybe a bad weights initialization?

I also did a brief investigation of the first FC layer, but see no obvious weird things...

[ddobbelaere]

Same observations on latest vdv net uploaded to fishtest (nn-535ee551b2cf.nnue). Some internal features of the quantized net seem dead/unused:

Unrelated idea that I have for a while: define the correlation between nets to be the maximum correlation over all permutations of the internal hidden variables. Do different runs with the same training parameters and input data lead to correlated nets/the same internal feature sets?

[Sopel97]

Or maybe the combination of training and input data had no way to extract any more useful features back then? Or maybe a bad weights initialization?

Could actually be initialization. Nodchip initializes the bias to 0.5 +- random. pytorch does 0 +- random.

[ddobbelaere]

Hmm, yeah that could explain things.

One of the things that is probably uncommon in our architecture (w.r.t. other nets for e.g. image recognition) is that our excitation is sparse (limited number of excited input features), which means that there is potentially not enough "input energy" to overcome a relatively large negative bias. If I am not mistaken (see e.g. https://stackoverflow.com/questions/48529625/in-pytorch-how-are-layer-weights-and-biases-initialized-by-default), both weights and biases are initialized in pytorch based on a uniform distribution with standard deviation inversely proportional to the square root of the total fan-in (which is much bigger than the typical effective fan-in).

This standard deviation for the biases is pretty small btw: 1/sqrt(64 * 641) = 0.0049 (normalized) or 127/sqrt(64*641) = 0.62702 (unnormalized).

This seems to explain the rather small observed negative biases (all of them are negative!) on the dead feature ReLUs. Note that this might explain why the weights are so small, they are just small from the beginning (initialization) onwards! A plausible explanation for the observations could be that the dead features are "trapped" in a dead state from the beginning onwards.

[Sopel97]

We tried to match nodchip initialization early on, especially because the fact that the input layer is very sparse as you mentioned, but the results were worse. We have not tried to change initialization only for the feature transformer. I think we should do it and see how the nets look like then.

[ddobbelaere]

The discovered dead neurons provide an explanation for the lower compressed file size, so closing this.