RSA 常见攻击方法整理

0. 对模数 n 的分解

• msieve
• yafu
• http://factordb.com/
• 利用公约数，对 2 个 n 有相同的公约数使用欧几里得算法

1. 已知p、q、e 求d

在一次RSA密钥对生成中，假设p=473398607161，q=4511491，e=17，求解出 d

可用脚本，也可用 gmpy2.invert(e,(p-1)*(q-1))

2. 已知n、e、密文 求明文

已知n=920139713，e=19，密文如下

752211152
274704164
18414022
.........
459788476
306220148

n 分解结果为 p=18443，q=49891 ，可求 d，再利用 c = pow(c,d,n) 可求明文

3. 已知私钥文件、密文 求明文

给出私钥文件 private 和密文 encdata

可在 kali 或 Ubuntu 使用 openssl 直接解密 openssl rsautl -decrypt -in endata -inkey private -out flag.txt

4. 已知公钥文件、密文 求明文

给出公钥文件 public.pem 和密文 flag.enc

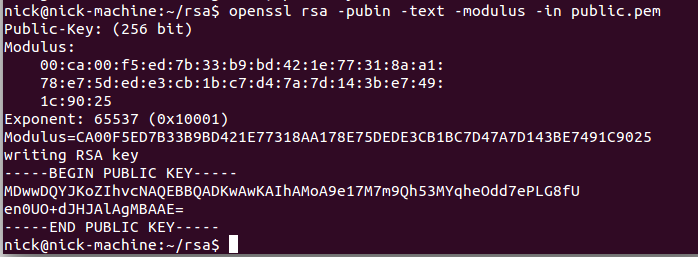
先分析公钥文件是否可以攻击，如果可以攻击会返回公钥信息 openssl rsa -pubin -text -modulus -in public.pem

获取模数 n=CA00F5ED7B33B9BD421E77318AA178E75DEDE3CB1BC7D47A7D143BE7491C9025

获取 e=65537

msieve 分解n msieve153.exe 0xCA00F5ED7B33B9BD421E77318AA178E75DEDE3CB1BC7D47A7D143BE7491C9025 -v

可以得到 p=290579950064240059571837821251441436997 q=314436328879392457343835667929324128609

利用 private.py 生成私钥文件，使用 openssl 即可 openssl rsautl -decrypt -in flag.enc -inkey private.pem -out res.txt

5. 利用n的公约数

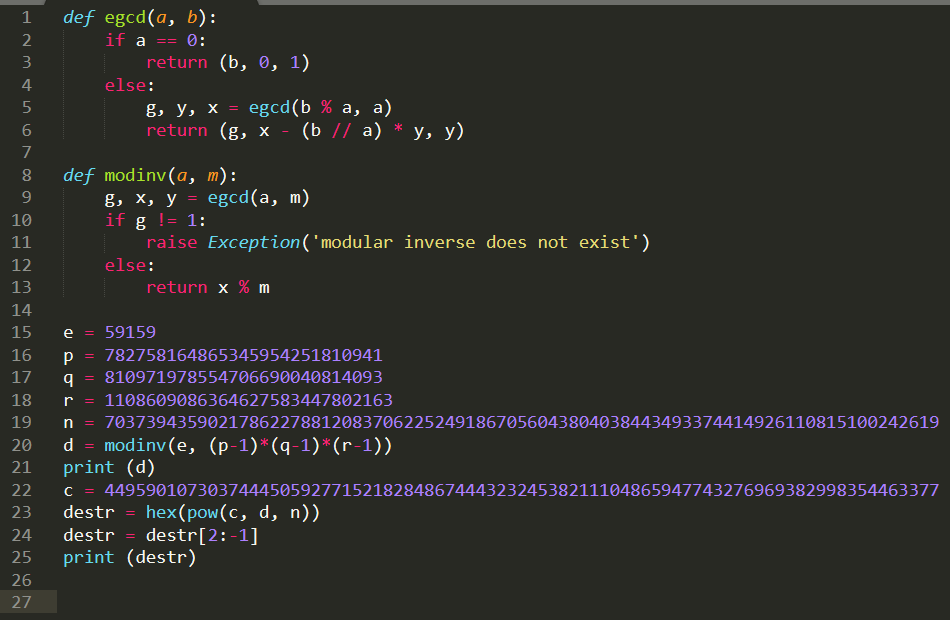
给出两个 n，共同密钥 e，两个密文，且两个 n 有公因子

假设 n1 和 n2 的公因子为 q，由 q 和 n1 求得 p1，已知 p1 和 q，可以求得 d1，已知enc1，d1，n1可以求得明文

6. 共模攻击

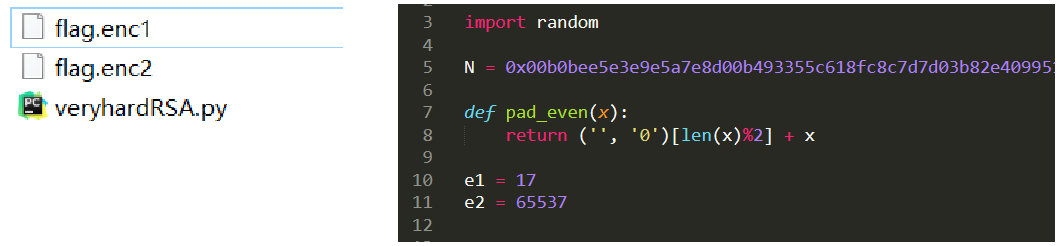
收到两份密文c1、c2，是一个明文 m 由相同的 n 和不同的2个 e(e1，e2) 进行加密的，此时无需求解出 d 即可破解出明文

7. 小明文攻击

即明文过小，导致明文的 e 次方仍然小于 n ，在 e=3 或 e 较小时可以首先尝试这种方法

给出 flag.enc 和 pubkey.pem，flag.enc 可以参照上一种情况读取内容，pubkey.pem 可以使用 openssl 获取内容

8. 低解密指数攻击(RSA-wiener-attack)

在 e 过大时使用，可以直接使用 RSAwienerHacker.py 求出 d

9. n 可被分解为多个素数

求 d 时，再修改一下欧拉函数值即可

10. dp 泄露攻击

给出 n、e、dp、c 时，可求 d

11. dp、dq 泄露攻击

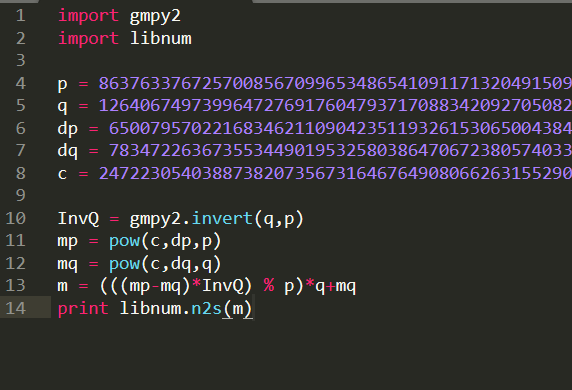
给出 dp、dq、p、q、c，可直接求出明文

12. 低加密指数广播攻击

工具&环境

• RSATool
• msieve
• yafu
• rsa-wiener-attack
• 求 d 的脚本 d.py
• 生成私钥文件的脚本 private.py
• 欧几里得算法求公约数 divisor.py
• 共模攻击脚本 common_mode.py
• 小明文攻击脚本 small_plaintext.py
• dp 泄露求 p q 脚本 dp_divulge.py
• dp dq 泄露求明文脚本 dpdq_divulge.py
• python2
  • binascii
  • gmpy2
  • pycrypto(Crypto)

一点点个人见解

个人发现的趋势

最近的比赛中有一个很明显的趋势，就是不再是单纯的考 RSA，而是结合其他数学问题，利用其他的数学问题求出 RSA 涉及到的变量