In this repository, you'll find an implementation of the probabilistic Greenberg-Hastings automaton. This implementation is the result of two years of my PhD with Prof. Dr. Leonardo P. Maia, where we were investigating neuronal avalanches from the point of view of a simple toy model that mimics basic features in neurodynamics. This model is based in some papers (Bornholdt & Röhl, Haldeman & Beggs - Phys. Rev., Copelli, Roque, Oliveira & Kinouchi, Kinouchi & Copelli - Nat Phys., T Mosqueiro & L Maia - Phys Rev E). I'm not just sharing the core code, but also a small example script to reproduce one of the figures shown in this paper. You can find this example in Example folder.
Although almost all comments are in portuguese, I plan to eventually translate it to english someday. This is not a priority though, especially because anyone can figure things out most of the time. If you are using this code, please (please!!) star this repository and cite T Mosqueiro & L Maia -- Phys Rev E v88 p012712.
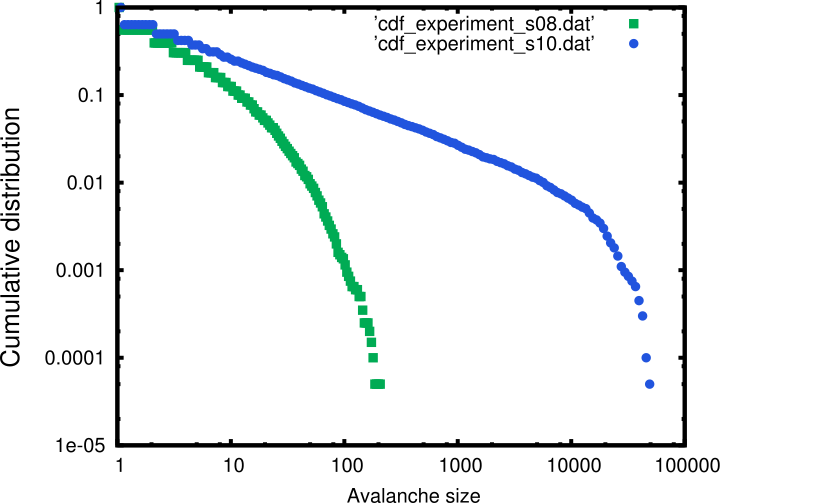
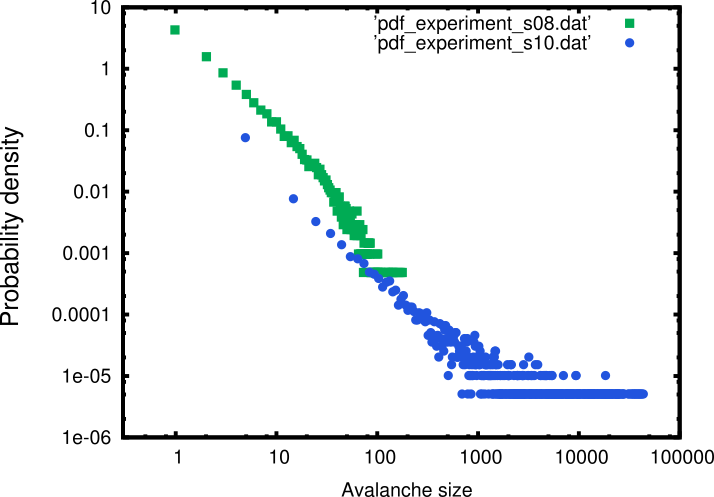
In the folder Example, you'll find a simple piece of code to illustrate how to simulate neuronal avalanches and plot them. The result looks like
These results show in green a subcritical avalanche distribution and in blue, a critical distribution. Inside Example folder, check Readme.md for more information.
There no real dependencies for the main code (everything that is in the core folder is self-contained). All you'll need is a fortran compiler, either Intel's or GCC.
However, to run the example in Example folder, you'll also need GnuPlot, texlife-epstopdf and python 2.7. Pypy is preferable.
tl;dr version: please, don't sue me and ship a copy of the License file with any derived product. Read License file for the actual terms.