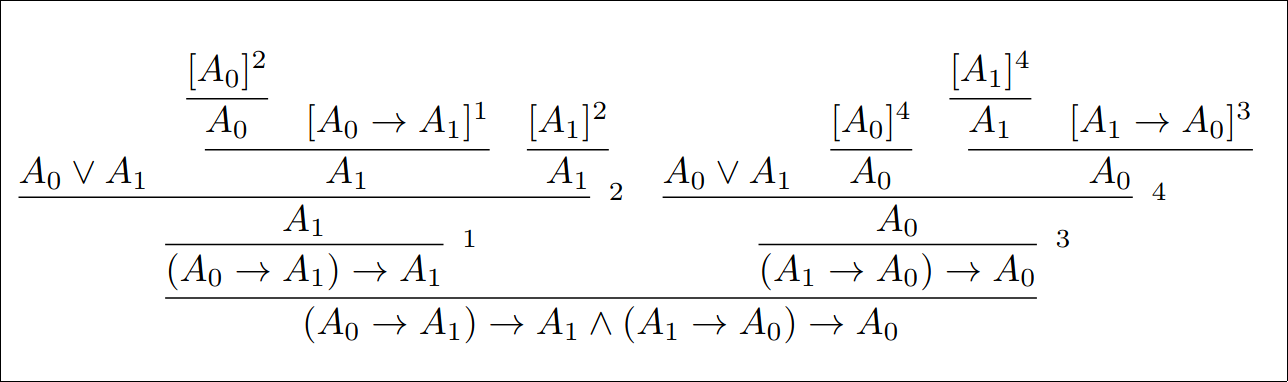A natural deduction prover in Gentzen's system.
Both the intuitionistic (proofNI) and the classical (proofNK) system are supported.
The output can be rendered in LaTeX using the lkproof package.
Suppose you want a proof for A0 ∨ A1 ⊢ ((A0 → A1) → A1) ∧ ((A1 → A0) → A0) in the intuitionistic system.
You can then run the following:
$ ghci Main.hs
> import Formula
> sequence_ $ printDeductionTree <$> proofNI (((Atom 0 --> Atom 1) --> Atom 1) /\ ((Atom 1 --> Atom 0) --> Atom 0)) [Atom 0 \/ Atom 1]
\infer
{(A_0 \rightarrow A_1) \rightarrow A_1 \land (A_1 \rightarrow A_0) \rightarrow A_0}
{
\infer[^1]
{(A_0 \rightarrow A_1) \rightarrow A_1}
{
\infer[^2]
{A_1}
{
A_0 \lor A_1
&
\infer
{A_1}
{
\infer
{A_0}
{
[A_0]^2
}
&
[A_0 \rightarrow A_1]^1
}
&
\infer
{A_1}
{
[A_1]^2
}
}
}
&
\infer[^3]
{(A_1 \rightarrow A_0) \rightarrow A_0}
{
\infer[^4]
{A_0}
{
A_0 \lor A_1
&
\infer
{A_0}
{
[A_0]^4
}
&
\infer
{A_0}
{
\infer
{A_1}
{
[A_1]^4
}
&
[A_1 \rightarrow A_0]^3
}
}
}
}The rendered output is:
- Introduction rules
- Elimination rules
- Extend to first order propositional logic