3939这里整理出我的并查集模板如下:
4040
4141``` CPP
42- int n = 1005 ; // 节点数量3 到 1000
43- int father[ 1005 ];
42+ int n = 1005 ; // n根据题目中节点数量而定,一般比节点数量大一点就好
43+ vector< int > father = vector< int > (n, 0 ); // C++里的一种数组结构
4444
4545// 并查集初始化
4646void init () {
@@ -50,40 +50,58 @@ void init() {
5050}
5151// 并查集里寻根的过程
5252int find (int u) {
53- return u == father[ u] ? u : father[ u] = find(father[ u] );
54- }
55- // 将v->u 这条边加入并查集
56- void join(int u, int v) {
57- u = find(u);
58- v = find(v);
59- if (u == v) return ;
60- father[ v] = u;
53+ return u == father[ u] ? u : father[ u] = find(father[ u] ); // 路径压缩
6154}
55+
6256// 判断 u 和 v是否找到同一个根
63- bool same (int u, int v) {
57+ bool isSame (int u, int v) {
6458 u = find(u);
6559 v = find(v);
6660 return u == v;
6761}
62+
63+ // 将v->u 这条边加入并查集
64+ void join(int u, int v) {
65+ u = find(u); // 寻找u的根
66+ v = find(v); // 寻找v的根
67+ if (u == v) return ; // 如果发现根相同,则说明在一个集合,不用两个节点相连直接返回
68+ father[ v] = u;
69+ }
70+
6871```
6972
70- 以上模板汇总, 只要修改 n 和father数组的大小就可以了 。
73+ 以上模板 只要修改 n 就可以了,本题 节点数量不会超过1000 。
7174
7275并查集主要有三个功能。
7376
74771. 寻找根节点,函数:find(int u),也就是判断这个节点的祖先节点是哪个
75782. 将两个节点接入到同一个集合,函数:join(int u, int v),将两个节点连在同一个根节点上
76- 3. 判断两个节点是否在同一个集合,函数:same (int u, int v),就是判断两个节点是不是同一个根节点
79+ 3. 判断两个节点是否在同一个集合,函数:isSame (int u, int v),就是判断两个节点是不是同一个根节点
7780
7881简单介绍并查集之后,我们再来看一下这道题目。
7982
80- 题目说是无向图,返回一条可以删去的边,使得结果图是一个有着N个节点的树。
83+ 题目说是无向图,返回一条可以删去的边,使得结果图是一个有着N个节点的树(即:只有一个根节点) 。
8184
8285如果有多个答案,则返回二维数组中最后出现的边。
8386
84- 那么我们就可以从前向后遍历每一条边,边的两个节点如果不在同一个集合,就加入集合(即:同一个根节点)。
87+ 那么我们就可以从前向后遍历每一条边(因为优先让前面的边连上),边的两个节点如果不在同一个集合,就加入集合(即:同一个根节点)。
88+
89+ 如图所示:
90+
91+ 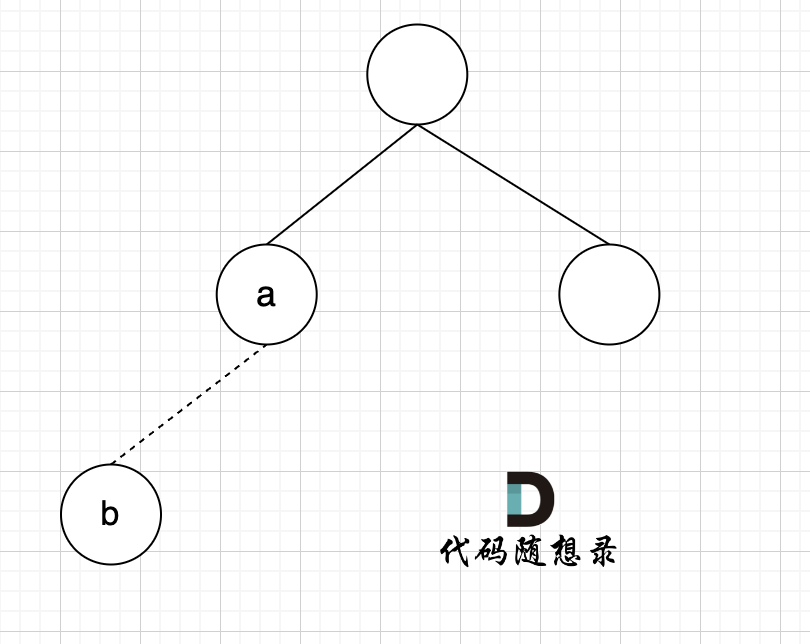
92+
93+ 节点A 和节点 B 不在同一个集合,那么就可以将两个 节点连在一起。
8594
86- 如果边的两个节点已经出现在同一个集合里,说明着边的两个节点已经连在一起了,如果再加入这条边一定就出现环了。
95+
96+ (如果题目中说:如果有多个答案,则返回二维数组中最前出现的边。 那我们就要 从后向前遍历每一条边了)
97+
98+ 如果边的两个节点已经出现在同一个集合里,说明着边的两个节点已经连在一起了,再加入这条边一定就出现环了。
99+
100+ 如图所示:
101+
102+ 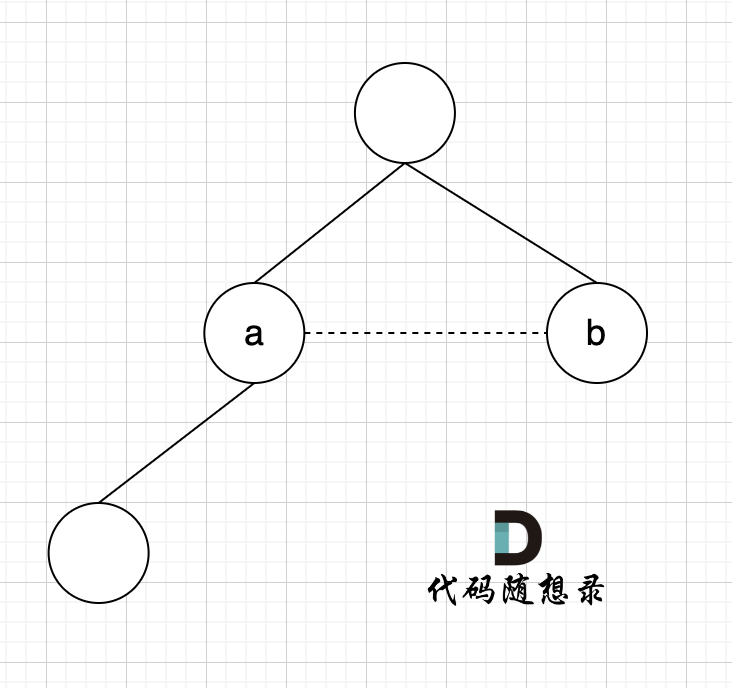
103+
104+ 已经判断 节点A 和 节点B 在在同一个集合(同一个根),如果将 节点A 和 节点B 连在一起就一定会出现环。
87105
88106这个思路清晰之后,代码就很好写了。
89107
@@ -93,7 +111,7 @@ bool same(int u, int v) {
93111class Solution {
94112private:
95113 int n = 1005; // 节点数量3 到 1000
96- int father[1005];
114+ vector< int> father = vector<int> (n, 0); // C++里的一种数组结构
97115
98116 // 并查集初始化
99117 void init() {
@@ -105,24 +123,22 @@ private:
105123 int find(int u) {
106124 return u == father[u] ? u : father[u] = find(father[u]);
107125 }
108- // 将v->u 这条边加入并查集
109- void join(int u, int v) {
110- u = find(u);
111- v = find(v);
112- if (u == v) return ;
113- father[v] = u;
114- }
115- // 判断 u 和 v是否找到同一个根,本题用不上
116- bool same(int u, int v) {
126+ // 判断 u 和 v是否找到同一个根
127+ bool isSame(int u, int v) {
117128 u = find(u);
118129 v = find(v);
119130 return u == v;
120131 }
132+ // 将v->u 这条边加入并查集
133+ void join(int u, int v) {
134+ if (isSame(u, v)) return ;
135+ father[v] = u;
136+ }
121137public:
122138 vector<int> findRedundantConnection(vector<vector<int>>& edges) {
123139 init();
124140 for (int i = 0; i < edges.size(); i++) {
125- if (same (edges[i][0], edges[i][1])) return edges[i];
141+ if (isSame (edges[i][0], edges[i][1])) return edges[i];
126142 else join(edges[i][0], edges[i][1]);
127143 }
128144 return {};
0 commit comments