Resources I love:
https://www.codenewbie.org/basecs
https://runestone.academy/runestone/books/published/pythonds/index.html
https://www.interviewbit.com/courses/programming/topics/dynamic-programming/
https://www.hackerearth.com/practice/algorithms/graphs/depth-first-search/tutorial/
https://app.codesignal.com/interview-practice https://courses.grainger.illinois.edu/cs225/fa2019/resources/
| Algorithm | Average Worst case |
|---|---|
| Space O(n) | O(n) |
| Search O(1) | O(n) |
| Insert O(1) | O(n) |
| Delete O(1) | O(n) |
□ Dictionary: Abstract Data Type (ADT)
○ Maintain set of items, each with a key
§ Insert(item)
§ Delete(item)
§ Search(key)
□ How to handle hash table collisions:
○ Chaining = linked list.
○ Open Addressing= All entry records
are stored in the bucket array itself.
# Function to count set bits in an integer
# in Python
def countSetBits(num):
# convert given number into binary
# output will be like bin(11)=0b1101
binary = bin(num)
# now separate out all 1's from binary string
# we need to skip starting two characters
# of binary string i.e; 0b
setBits = [ones for ones in binary[2:] if ones=='1']
print len(setBits)
# Driver program
if __name__ == "__main__":
num = 11
countSetBits(num)
2^0, 2^1, 2^2, 2^3, 2^4, 2^5, 2^6, 2^7 = 8 bits = 1 byte
2^7 2^6 2^5 2^4 2^3 2^2 2^1 2^0
| 128| 64 | 32| 16 | 8 | 4 | 2 | 1 |
def set_bit(x, position):
mask = 1 << position
return x | mask
x = 00000110
position = 00000101
mask = 00100000
calculation:
x 00000110
mask 00100000
output = 00100110
sef clear_bit(x, position):
mask = 1 << position
return x & ~mask
x 00000110
position 00000010
mask 00000100
~mask 11111011
x 00000110
& ~mask 11111011
00000010
def flip_bit(x, position):
mask = 1 << position
return x ^ mask
x 01100110
position 00000010
mask 00000100
x 01100110
^ mask 00000100
----------------
01100010
Shift the binary digits by n, pad 0's on the right
Each shift is a multiply by 2 (unless there's overflow)
Shift the binary digits by n, pad 0's on the left
Each shift is a divide by 2 with round towards negative infinity
def is_bit_set(x, position):
shifted = x >> position
return shifted & 1
X 01100110 00000011 shifted
Position 00000101 & 00000001 1
Shifted 00000011 00000001
Even: check the right-most bit
(x & 1) == 0
CHECK IF POWER OF TWO
1000
(x & x-1) == 0 & 0111
0000
Write a function to count the number of Bits that are different between two numbers
def num_diff_bits(a, b):
count = 0
diff = a ^ b
while diff != 0:
if diff & 1:
count += 1
diff = diff >> 1
return count
http://bits.stephan-brumme.com/ http://h14s.p5r.org/2012/09/0x5f3759df.html
http://en.wikipedia.org/wiki/Fast_inverse_square_root
https://bits.stephan-brumme.com/
https://graphics.stanford.edu/~seander/bithacks.html
>>> bin(0b1111 << 1)
'0b11110'
>>> bin(0b1111 << 2)
'0b111100'
>>> bin(0b1111 << 3)
'0b1111000'
>>> bin(0b1111 << 4)
'0b11110000'
- https://wiki.python.org/moin/BitwiseOperators
- https://wiki.python.org/moin/BitManipulation
- https://stackoverflow.com/questions/109023/how-to-count-the-number-of-set-bits-in-a-32-bit-integer
- https://bits.stephan-brumme.com/swap.html
- https://bits.stephan-brumme.com/absInteger.html
- https://www.youtube.com/watch?v=Hzuzo9NJrlc&feature=youtu.be
Height(tree)
if tree == nil: return 0
return 1 + Max(Height(tree.left),Height(tree.right))
Size(tree)
if tree == nil: return 0
return 1 + Size(tree.left) + Size(tree.right)
DFS
- Time complexity: O(n)
- Space complexity: best: O(log n) - avg. height of tree worst: O(n)
- Inorder (DFS: left, self, right)
- Postorder (DFS: left, right, self)
- Preorder (DFS: self, left, right)
In-order: This is InOrderTraversal is what we might use to print all the nodes of a binary search tree in alphabetical order.
InOrder(tree)
if tree == nil: return
InOrder(tree.left)
print(tree.key)
InOrder(tree.right)
In a post-order traversal, we evaluate all children fully before evaluating a node itself.
PostOrder(tree)
if tree == nil: return
PostOrder(tree.left)
PostOrder(tree.right)
print(tree.key)
In a pre-order traversal, we evaluate the node fully before evaluating a node's children.
PreOrder(tree)
if tree == nil: return
print(tree.key)
PreOrder(tree.left)
PreOrder(tree.right)
BFS
- Time complexity: O(n)
- Space complexity: best: O(1), worst: O(n/2)=O(n)
levelTransversal(tree)
if tree == nil: return
Queue q
q.Enqueue(tree) //put root of tree in queue
while not q.Empty():
node <- q.Dequeue() // while queue is not empty, we're going to pull a node off
print(node)
if node.left =/= nil: // if left child exists, queue it
q.Enqueue(node.left)
if node.right =/= nil:
q.Enqueue(node.right) //if right child exists, queue it
Problem:
BFS - is the given Tree a valid Binary Search Tree?
"""
Node is defined as
class node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
"""
import queue
def checkBST(root):
diff = 0
q = queue.Queue()
if root == None:
return False
q.put(root)
while not q.empty():
node = q.get()
node_val = node.data
if node.left != None:
l = node.left
l_val = l.data
diff = abs(node_val - l_val)
if l_val > node_val:
return False
q.put(l)
if node.right != None:
r = node.right
r_val = r.data
if (r_val - node_val) != diff:
return False
if r_val < node_val:
return False
q.put(r)
return True
Average O(log n) searching, insertion, deletion
Worst O(n) searching, insertion, deletion
Space O(n)
BST array representation:
If node is at index i
Its left-child is at 2*i + 1
Its right-child is at 2*i + 2
Its parent is at (i -2) // 2
Bubble up: halving the index every time you move element up the tree
AVL
The difference in height between left and right must always be <= 1
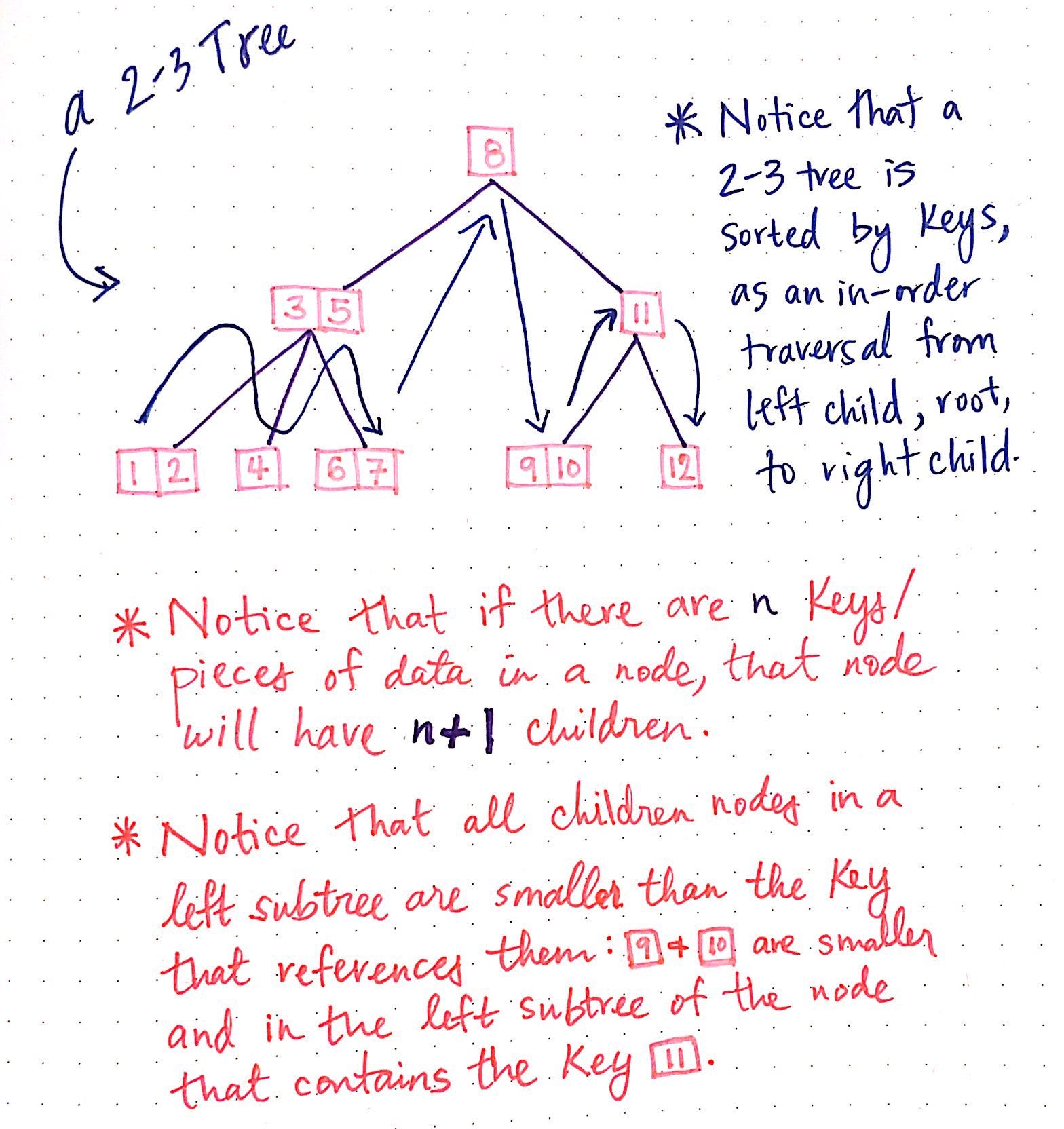
2-3 Tree
B-Tree
- A node can have more than 2 child nodes
- It's self-balancing b-trees
Every pointer has a pointer to a child-node as well as a pointer to a record (in disk). Useful for implementing multi-level indexing.
-
Heap
-
Insert & Delete
Insert element in leaf and adjusting upwards. Delete element in root, move leaf descendant to root while maintaining balanced tree, then adjust new root by comparing it with its descendants. Maintain min/max heap nature.
-
Heap Sort
Create heap, delete root
-
Heapify
The process of converting a binary tree into a Heap data structure.
-
Priority Queue
Binary Heap construction O(n)
Polling/removing O(log(n))
Peeking/seeing at root O(1)
Adding O(log(n))