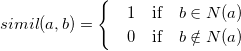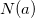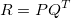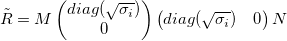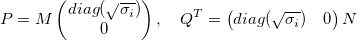Open Music Recommendation System (Open MRS) by BerryAI

Acai is an open source project initialised by Berry Labs, a startup working towards machine learning algorithms to solve daily issues. Acai (codename) is trying to solve the problem of The Tyranny of Choice (a.k.a Paradox of Choice) to describe the misery of users facing over-abundant choices. In the music area, especially in the age of streaming music, this paradox becomes so significant that it affects every single piece of choice when users try to enjoy music. It's why this project was born. http://www.acai.berry.ai/

Getting Started

These instructions will get you a copy of the project up and running on your local machine for development and testing purposes. See deployment for notes on how to deploy the project on a live system.

Prerequisites Software

What things you need to install the software and how to install them

Python
Python-Librosa
Python-Lutorpy
Python-NumPy
Python-Scipy
Torch
Torch-cunn
Torch-dp
Torch-nn
Torch-optim
Torch-xlua

Linux

All major distributions of Linux provide packages for both Python and NumPy.

Mac OS X

pip install librosa
pip install lutorpy
pip install numpy
pip install scipy

Windows

Personally, I will recommend Anaconda as default Python compiler. To install them, go to page

https://www.continuum.io/downloads

and find the proper install packages

Torch

You can find torch installation instruction in the official site: http://torch.ch/ You can also refer to our wiki page: https://github.com/BerryAI/music_cortex/wiki/Torch-Setup

Prerequisites Dataset

In this project, we use some public open database, and they are

• Last.fm 1k user data download
• Million Song Databasedownload
• Million Song Database subset download
• Echo Nest user data download

For convenience purpose, I have calculate the intersection between 1k user data and MSD Database. HERE is the download link.

Installation

Usage

Test functions are under ./test folder. After downloading all the data files, please put the extracted files into ./data folder.

Then run collaborative filtering

python test_cf_hf_gd.py

run convolutional neural networks

th example.lua

in command line under the directory of the project installed.

Algorithms included:

Collaborative Filtering Methods

* Memory based recommendation

The recommendation equation is:

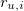
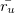
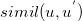
Where U is the full set of all users, is user u's rating score of item i, and is the average rating score for user u. For similarity function , we have two approaching ways:

1. K nearest neighbours:
   Where is the set of neighbors of user a.
2. Pearson Correlation:
   

* Matrix Factorization and Hidden Features

We could use much smaller dimension matrix P, Q to represent and approximate the full rating score matrix R. That is:

Normally, we have two different approaches:

1. Singular Value Decomposition

R is a m*n matrix

Where:

• M is m*m unitary matrix
• Σ is m*n diagonal matrix with singular values
• N is n*n unitary matrix

With first k singular values, we could approximate R as:

Then:

2. Gradient Descent We try to minimize the norm of residue matrix:
   

we have two different approaches:

• Classic Gradient Descent:
  

• Stochastic Gradient Descent with momentum:
  

Both methods will converge, but please be careful choosing coefficients.

Convolutional Neural Networks

* Building Blocks

1.Convolutional Layer Convolutional layers are the core building block of CNNs. The layer's parameters consist of sets of learnable filters/kernels . During training, the parameters are learned from data in order to solve the target problem. The forward equation is:
where is the data in layer L in filter i, and * represents convolution operation.

2.Max Pooling Layer Pooling layer is another important concept of CNN. It is down-sampling process. Max pooling is a non-linear down-sampling method. The forward equation is:
where p,q are the pooling size.

3.Rectified Linear Units Layer ReLU layers apply nonlinear activation function to neurons. Comparing to other common activation functions, ReLU is fast in training and suffers less on gradient extenuation during training.The forward equation is:

4.Loss Layer The loss layer is the last layer in CNN which defines the training deviation between real predicted results and target results. We provide 2 options in our model.

• Mean Squared Error where is real output and is target output.

• Softmax Loss where is real output and is target output.

* Back-propagation Rule

• Stochastic Gradient Descent with momentum:
  

Contributing

1. Fork it!
2. Create your feature branch: git checkout -b my-new-feature
3. Commit your changes: git commit -am 'Add some feature'
4. Push to the branch: git push origin my-new-feature
5. Submit a pull request :D

License

The OpenMRS source code and binaries are released under the MIT license