You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
Hello,
I tried using the adjoint-family integrators to obtain sensitivities of an arbitrary cost functional
w.r.t. interpolation parameters of a linear system
with a linearly interpolated input (using three points) and compared it to the finite difference approximation of the problem. (I attached some commented matlab code as a .zip-file. Use Matlab->Publish->Publish to get a LaTeX-formatted file of the problem and its Jacobians etc.) The sensitivities differ so much that I suspected the finite difference approximation to be wrong. Because of this, I tried implementing a "brute-force" forward sensitivity analysis aswell as an adjoint sensitivity analysis in ode45 by solving the forward sensitivity equations simultaneously and the backward problem after I obtained the forward solution, respectively (this is not included in the minimal working example in the zip file). They both gave the same solution as the finite difference approximation. Interestingly, though, the quadrature value in MATLODE is the same as int_ryp (in provided file) which I calculated numerically using trapz.
In short:
MATLODE output Quadrature after the solver call is Quad = 64.3645 => same as above with trapz!
Finite difference sensitivity
MATLODE sensitivity
=> differ significantly?!
Am I missing something here?
Thank you in advance.
Hi @sh-cau, thanks for providing a minimal example to test. I checked in Mathematica to see if the FD version is correct, and indeed it is. We're going through the code now to see if there is a mistake in the config or with MATLODE.
Thank you @Steven-Roberts,
your help is, again, very much appreciated. Thank you also for providing the mathematica file. I was so into numerical methods that it did not come to my mind to check analytically...
Hello,
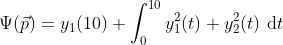
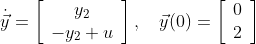
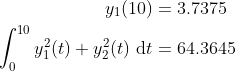
I tried using the adjoint-family integrators to obtain sensitivities of an arbitrary cost functional
w.r.t. interpolation parameters of a linear system
with a linearly interpolated input (using three points) and compared it to the finite difference approximation of the problem. (I attached some commented matlab code as a .zip-file. Use Matlab->Publish->Publish to get a LaTeX-formatted file of the problem and its Jacobians etc.) The sensitivities differ so much that I suspected the finite difference approximation to be wrong. Because of this, I tried implementing a "brute-force" forward sensitivity analysis aswell as an adjoint sensitivity analysis in ode45 by solving the forward sensitivity equations simultaneously and the backward problem after I obtained the forward solution, respectively (this is not included in the minimal working example in the zip file). They both gave the same solution as the finite difference approximation. Interestingly, though, the quadrature value in MATLODE is the same as
int_ryp(in provided file) which I calculated numerically usingtrapz.In short:
MATLODE output
Quadratureafter the solver call isQuad = 64.3645=> same as above withtrapz!Finite difference sensitivity
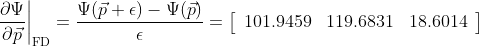
MATLODE sensitivity
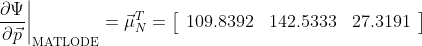
=> differ significantly?!
Am I missing something here?
Thank you in advance.
mweMatloteIssue.zip
EDIT: included formated LaTeX here additionally to the matlab comments.
The text was updated successfully, but these errors were encountered: