Progetto per l'esame di Programmazione Concorrente e Parallela su Cloud.
- Studente: Tesauro Emmanuel
- Matricola: 0522500988
- MD5: 4bc390e61c1cd2a4001199d94b8d334d
- Amazon EC2 instance type: t2.2xlarge
- Introduzione: breve introduzione al problema
- Descrizione della soluzione: analisi della soluzione adottata
- Struttura del progetto: come è organizzato il progetto
- Istruzioni per l'esecuzione: cosa fare per eseguire il programma
- Dettagli dell'implementazione: analisi dettagliata del codice
- Discussione sulla correttezza: discussione circa la correttezza dell'algoritmo
- Benchmarks: benchmarks finali
Il modello di segregazione di Schelling è un modello agent-based che dimostra che avere persone con una preferenza "lieve" all'interno del proprio gruppo nei confronti nel gruppo stesso, porta inevitabilmente ad una società segregata.
L'obiettivo di tale progetto è quello di implementare il modello di segregazione di Schelling creando un programma scritto in linguaggio C ed utilizzando la libreria Open MPI.
Viene fornito un unico file (Schelling.c) che necessita di essere prima compilato e, poi, eseguito.
Al suo interno è possibile definire la grandezza della matrice di partenza a proprio piacimento, in quanto l'algoritmo lavora con matrici di qualsiasi dimensione.
La soluzione sviluppata segue 8 passi ben definiti.
-
Il Master inizializza la matrice utilizzando le costanti definite all'interno del programma. Di default, questi valori sono:
// #region Matrice #define ROWS 100 // Numero di righe della matrice #define COLUMNS 100 // Numero di colonne della matrice // #endregion // #region Agenti #define AGENT_X 'X' // Agente X (BLU) #define AGENT_O 'O' // Agente O (ROSSI) #define EMPTY ' ' // Casella vuota (' ') #define AGENT_X_PERCENTAGE 30 // Percentuale di agenti X (blu) all'interno della matrice #define AGENT_O_PERCENTAGE 30 // Percentuale di agenti O (rossi) all'interno della matrice #define SATISFIED_PERCENTAGE 33.333 // Percentuale di soddisfazione di un agente // #endregion
-
Suddivisione della matrice per numero di righe tra i vari processi
-
Scambio delle righe tra i processi adiacenti per il calcolo della soddisfazione (locale) degli agenti della sottomatrice (la prima riga con il processo precedente e l'ultima riga con il processo successivo).
-
Calcolo della soddisfazione di ogni agente della sottomatrice
-
Calcolo del numero di celle vuote di ogni sottomatrice e delle posizioni in cui sono situate
-
Scambio delle posizioni calcolate al punto precedente tra tutti i processi per l'assegnazione delle celle di destinazione in cui gli agenti possono spostarsi
-
Spostamento degli agenti
-
Recupero della matrice finale per calcolare la soddisfazione globale
Nota: I punti 3-7 vengono ripetuti per un numero di volte pari MAX_STEP (di default pari a 100).
- src/
- Schelling_MPI.c: file contenente il codice sorgente del programma
- files_out/
- Schelling_MPI.out: file eseguibile del programma
- doc/
- benchmarks.md: file di report di tutti i test effettuati
- img/: cartella contente le immagini per la documentazione
Dalla root del progetto:
-
Compilare il programma con
mpicc src/Schelling_MPI.c -o files_out/Schelling_MPI.out
-
Eseguire il programma con
mpirun --allow-run-as-root --mca btl_vader_single_copy_mechanism none -np X files_out/Schelling_MPI.out
dove 'X' è un numero intero.
La matrice viene inizializzata dal Master in base ai parametri definiti all'interno del codice sorgente del programma.
L'agente da inserire in una cella [i][j] della matrice viene determinato calcolando un numero casuale num tra 0 e 99 e si inserisce:
- X -> se 0 ≤ num < AGENT_X_PERCENTAGE
- O -> se AGENT_X_PERCENTAGE ≤ num < AGENT_X_PERCENTAGE + AGENT_O_PERCENTAGE
- EMPTY (' ') -> se AGENT_X_PERCENTAGE + AGENT_O_PERCENTAGE ≤ num < 100
Le uniche regole da rispettare sono:
- La somma della percentuale di probabilità di avere un agente 'X' o 'O' all'interno della matrice non deve superare 99
- Non è possibile creare una matrice con un numero di righe maggiore del numero di processi con cui si decide di eseguire il programma
Tutti i processi calcolano quante righe della matrice dovranno ricevere. Questo significa che ogni processo si occuperà di 'numero di righe ricevute × numero di colonne' elementi.
In base al numero di righe della matrice di partenza e al numero di processi con cui si esegue il programma, viene effettuata la divisione tra questi due valori e se il 'resto > 0' viene assegnata una riga in più al processo in questione.
Inoltre, sono state assegnate ulteriori 2 righe ai processi con 'rank > 0' e 'rank < world_size-1' e solo una ulteriore riga ai processi con 'rank == 0' e 'rank == world_size - 1' per 'ospitare' le righe dei processi adiacenti.
Nota: I processi con 'rank == 0' e 'rank == world_size - 1' ricevono una singola riga in più perchè si è scelto di non implementare la matrice come una struttura circolare e, quindi, questi processi non sono vicini.
A questo punto, la matrice è stata suddivisa utilizzando la funzione MPI_Scatterv();
// Calcolo della porzione della matrice da assegnare a ciascun processo
subdivide_matrix(world_size, displacements, sendcounts, rows_per_process);
// Suddivisione delle righe tra i processi
sub_matrix = malloc(rows_per_process[rank] * COLUMNS * sizeof(char *));
MPI_Scatterv(matrix, sendcounts, displacements, MPI_CHAR, sub_matrix, rows_per_process[rank] * COLUMNS, MPI_CHAR, ROOT, MPI_COMM_WORLD);Una volta che ogni processo ha ricevuto la propria porzione di matrice, si procede calcolando la soddisfazione di ogni agente all'interno di quest'ultima.
Per fare ciò, è stato necessario scambiare le proprie righe più esterne con i processi adiacenti, come mostra il seguente snippet:
if (rank != 0) {
MPI_Isend(sub_matrix, COLUMNS, MPI_CHAR, neighbour_down, 99, communicator, &request_up);
MPI_Irecv(sub_matrix + neighbour_down_row_pos, COLUMNS, MPI_CHAR, neighbour_down, 99, communicator, &request_up);
}
if (rank != world_size - 1) {
MPI_Isend(sub_matrix + my_last_row_pos, COLUMNS, MPI_CHAR, neighbour_up, 99, communicator, &request_down);
MPI_Irecv(sub_matrix + neighbour_up_row_pos, COLUMNS, MPI_CHAR, neighbour_up, 99, communicator, &request_down);
}Il calcolo della soddisfazione restituisce una nuova matrice di dimensioni esattamente uguali a quelle della sottomatrice senza le righe aggiuntive. Il motivo per cui si è scelto questo tipo di implementazione sta nel fatto che questa nuova matrice (want_move) verrà utilizzata successivamente quando verranno effettuati gli spostamenti degli agenti che non sono soddisfatti.
Questa matrice, è formata da un intero per ogni cella [i][j]:
- 0 -> l'agente è soddisfatto e NON vuole spostarsi
- 1 -> l'agente NON è soddisfatto e vuole spostarsi
- -1 -> la cella in questione è vuota ed è utilizzabile per ospitare agenti che vogliono muoversi
Ogni agente è soddisfatto se intorno a lui ha almeno il 33.333% di agenti simili. Questo vuol dire che le celle contenenti l'agente opposto oppure quelle vuote sono considerate non corrette. Nel caso in cui un agente si trovi in un bordo della matrice, ovviamente i vicini saranno di meno.
Il calcolo delle celle di destinazione è stato eseguito attraverso una chiamata alla funzione MPI_Allgatherv, dove ogni processo ha condiviso con tutti gli altri sia il numero di celle vuote che lui aveva in quel momento, sia le loro posizioni.
// Metto tutte le celle vuote della matrice insieme
MPI_Allgatherv(local_void_cells, number_of_local_void_cells, datatype, global_void_cells, number_of_global_void_cells, displacements, datatype, MPI_COMM_WORLD);A questo punto, l'array contenente le celle vuote di tutti i processi (global_void_cells) è stato mescolato e suddiviso equamente tra i processi. 'Equamente' significa che se un processo non avesse avuto alcun agente insoddisfatto, allora non avrebbe ricevuto una porzione di questo array perchè non avrebbe avuto bisogno.
// Suddivido l'array contenente le celle di destinazione per gli spostamenti
MPI_Scatterv(global_void_cells, void_cells_per_process, displacements, datatype, toReturn, void_cells_per_process[rank], datatype, ROOT, MPI_COMM_WORLD);Una volta che ogni processo sa quante e quali celle vuote di destinazione gli sono state assegnate, è stato possibile iniziare gli spostamenti degli agenti insoddisfatti.
L'idea che si è seguita è la seguente, ovvero, per un processo 'i':
-
Se la riga della cella di destinazione è una riga della mia sottomatrice (i == rank), allora posso effettuare lo spostamento senza dover effettuare comunicazione con altri processi.
// * Sono io -> lo sposto direttamente if (receiver == rank) { int startRow = displacements[rank]; // Mia riga iniziale int destRow = destination.row_index - startRow; // Mia riga di destinazione sub_matrix[destRow + destination.column_index] = sub_matrix[i * COLUMNS + j]; // Sposta l'agente sub_matrix[i * COLUMNS + j] = EMPTY; // Liberalo lo spazio nella sottomatrice want_move[destRow + destination.column_index] = 0; // Non rendere più disponibile lo spazio disponibile per altri want_move[i * COLUMNS + j] = -1; // Libera questo spazio }
-
Se la riga della cella di destinazione NON è una riga della mia sottomatrice (i != rank), allora non posso direttamente effettuare lo spostamento.
È stata creata una matrice che contiene sulle righe i processi (0, 1, ...) e sulle colonne la cella di destinazione dell'agente che vuole spostarsi ({ row, col, agent }), in modo tale da sapere, per qualsiasi processo, sia quanti elementi dovrà inviare agli altri processi, sia in quali posizioni dovranno essere salvati gli agenti.// * Altrimenti impacchetto tutto else { int startRow = displacements[receiver]; // Riga iniziale del destinatario int destRow = destination.row_index - startRow; // Riga di destinazione del destinatario moveAgent var = { destRow, destination.column_index, sub_matrix[i * COLUMNS + j] }; // {riga di destinazione, colonna di destinazione, agente da scrivere } data[receiver][num_elems_to_send_to[receiver]] = var; // Setto, al processo 'receiver', la X-esima colonna con la cella di destinazione dell'agente num_elems_to_send_to[receiver] += 1; //Aggiorno il numero di elementi che devo mandare al processo 'receiver' sub_matrix[i * COLUMNS + j] = EMPTY; // Libera lo spazio nella sottomatrice want_move[i * COLUMNS + j] = -1; // Libera questo spazio precedente }
Dopo aver 'impacchettato' tutto, è necessaria una fase di sincronizzazione tra tutti i processi, in modo tale che ogni processo possa ricevere da tutti gli altri gli agenti da scrivere nelle proprie celle e le posizioni in cui farlo.
// * Sincronizzo tutti i processi synchronize(rank, world_size, num_elems_to_send_to, num_assigned_void_cells, data, original_rows, sub_matrix, move_agent_type);
La correttezza per questo tipo di problema deve essere dimostrata, per ogni test, a partire dalla stessa matrice iniziale. È stato necessario, quindi, crearne una ad hoc per questa dimostrazione in quanto, normalmente, le matrici vengono inizializzate in maniera casuale.
Si procederà utilizzando una matrice 10x10 e si dimostrerà che, a parità di input, l'esecuzione con lo stesso numero di processi produrrà sempre la stessa matrice finale.
Inoltre, utilizzando una matrice 50x80 per una maggior evidenza, si dimostrerà che si verranno a formare gruppi ben definiti di agenti.
La caratteristiche che porta ad avere sempre la stessa matrice finale a partire sempre dalla stessa matrice iniziale è possibile ottenerla grazie ad una divisione ben definita sia del carico di lavoro, sia ad una suddivisione delle celle libere dove spostare gli agenti.
In particolare, la strada che si è scelto di seguire è stata quella di suddividere la matrice tra i processi in base al numero di righe della matrice stessa e di distribuire le celle libere dove spostare gli agenti prima calcolandole e, poi, facendo 'mescolare' ad ogni processo l'array contenente tutte queste celle utilizzando un seme definito come costante.
#define SEED 15
...
// Mischio l'array (uso lo STESSO seme per ogni processo in modo da avere lo shuffle uguale)
srand(SEED);
for (int i = 0; i < number_of_total_void_cells; i++) {
int destination = RAND(0, number_of_total_void_cells);
voidCell tmp = global_void_cells[destination];
global_void_cells[destination] = global_void_cells[i];
global_void_cells[i] = tmp;
}| Prima esecuzione con 2 processi | Seconda esecuzione con 2 processi | Prima esecuzione con 3 processi | Seconda esecuzione con 3 processi |
|---|---|---|---|
 |
 |
 |
 |
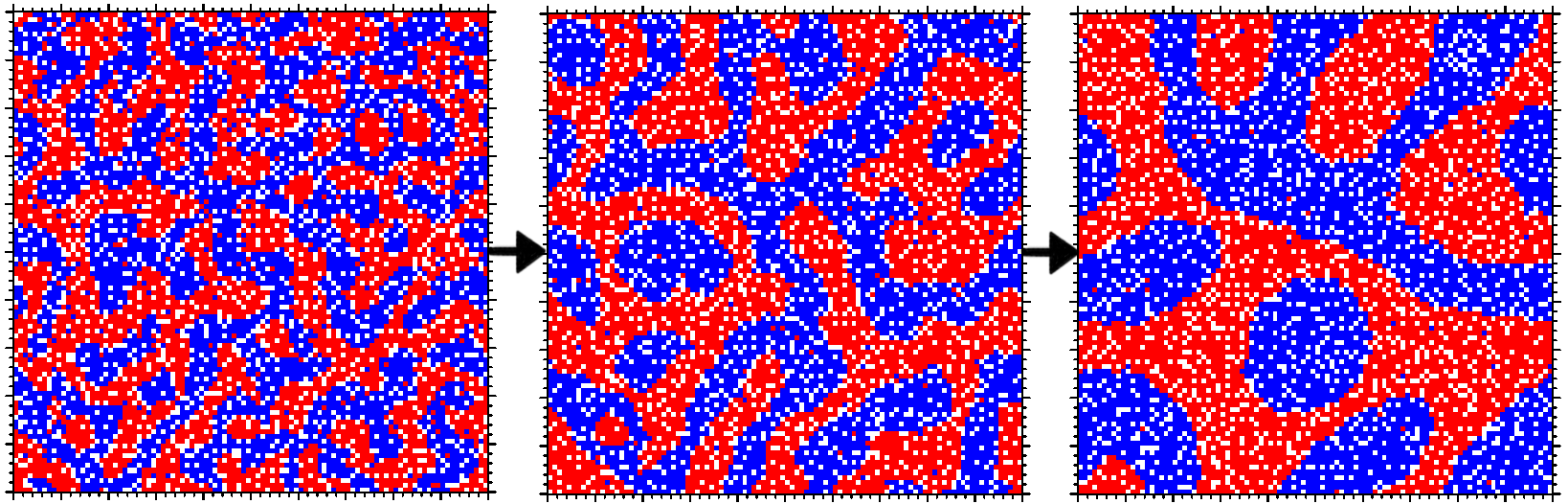
L'obiettivo di questo problema è quello di implementare il modello di segregazione di Schelling e, quindi, quello di mostrare come pian piano si vengono a formare gruppi di 'agenti' simili.
Per fare ciò, di seguito vengono riportate due immagini che mostrano la matrice iniziale e quella finale dopo aver eseguito 100 iterazioni.
| Matrice iniziale | Matrice finale |
|---|---|
 |
 |
I test sono stati effettuati su un cluster AWS composto da 4 istanze t2.2xlarge.
Per valutare l'efficienza dell'esecuzione parallela per questo tipo di problema, prenderemo in considerazione tre metriche: la speedup, la scalabilità forte e la scalabilità debole.
Tutti i test e i relativi risultati sono disponibili qui.
La speedup è una misura che indica il vantaggio nel risolvere un determinato problema utilizzando la computazione parallela. Il valore è definito come il rapporto tra il tempo impiegato per risolvere il problema su un singolo elemento di computazione (sequenziale) e il tempo impiegato per risolverlo su un computer o un sistema informatico in modo parallelo con p elementi di elaborazione identici.
Dato un input I di dimensione n, il tempo della soluzione sequenziale su input I è indicato come T(1,n) e il tempo della soluzione parallela su input I è indicato come T(p,n).
La speedup viene calcolata come S(p,n)=T(1,n)/T(p,n).
| 100x100 | 100x100 (zoom) |
|---|---|
 |
 |
| 1000x1000 | 1000x1000 (zoom) |
|---|---|
 |
 |
| 2500x2500 | 2500x2500 (zoom) |
|---|---|
 |
 |
| 5000x5000 | 5000x5000 (zoom) |
|---|---|
 |
 |
| Weak Speedup |
|---|
 |
I risultati mostrano che il trend è più o meno sempre lo stesso, ovvero che la speedup aumenta quando il calcolo parallelo viene effettuato sulla stessa macchina ma diminuisce quando si passa su macchine diverse.
Questa caratteristica è dovuta al fatto che la comunicazione tra i vari processi situati su macchine diverse è più dispendiosa in termini di tempo rispetto a quella che avviene all'interno della stessa macchina. Per come è stata implementata la soluzione e per come si può osservare dai grafici precedenti, l'algoritmo lavora molto bene in locale con 8 processi (pari al numero massimo di vCPUs per una singola istanza t2.2xlarge).
Inoltre, questo accade anche perchè ad ogni iterazione dell'algoritmo c'è bisogno di una fase di sincronizzazione in cui ogni processo invia tutto ciò che serve a tutti gli altri processi. Ovviamente, per quanto detto pocanzi, questa fase è molto dispendiosa.
Per scalabilità forte si intende il modo in cui il tempo di soluzione varia con il numero di processori per una dimensione fissa del problema.
I test sono stati eseguiti con un numero di processori pari a 1, 2, 4, 8, 12, 16, 20, 24, 28, 32 e su 4 inputi: 100x100, 1000x1000, 2500x2500, 5000x5000.
Generalmente, l'ideale sarebbe che il tempo di esecuzione diminuisca con l'aumentare dei processori in modo tale da distribuire il carico di lavoro su ognuno di essi. Questo, però, non è sempre possibile per quanto detto precedentemente, ovvero che ci potrebbero essere alcune tipologie di problemi in cui la soluzione parallela-distribuita funzioni peggio rispetto alla soluzione parallela su una singola macchina.
I grafici seguenti rispecchiano esattamente quanto detto finora.
| 100x100 | 1000x1000 |
|---|---|
 |
 |
| 2500x2500 | 5000x5000 |
|---|---|
 |
 |
I grafici, quindi, evidenziano come la soluzione parallela su singola macchina faccia diminuire il tempo di esecuzione anche della metà, ma quando si passa alla computazione distribuita i tempi crescono notevolmente per colpa della comunicazione onerosa.
Per scalabilità debole si intende il modo in cui il tempo di soluzione varia con il numero di processori per una dimensione fissa del problema per processore.
Questo significa che se il test con un numero di processori pari ad 1 fosse stato eseguito con una matrice 100x100 (#elementi = 10000), allora il test con 2 processori sarebbe dovuto ... con una matrice 200x100 o 100x200 (#elementi = 20000) per avere esattamente il doppio degli elementi e una suddivisione di 10000 elementi per processore.
Generalmente, l'ideale sarebbe che il tempo di esecuzione rimanga lineare all'aumentare della grandezza del problema e del numero di processori ma, come si può osservare dal seguente grafico, questo non succede.
Anche qui, questo è dovuto alla grande richiesta di comunicazione tra i vari processori sia per scambiarsi le righe di confine e le celle vuote, sia per la fase di sincronizzazione.