MinCq Learning Algorithm

This is a simple implementation of MinCq, a learning algorithm inspired by the PAC-Bayesian theory.

MinCq was first introduced in [1], but an upcoming journal paper will present an extensive and complete analysis of majority votes, PAC-Bayesian theory for inductive binary classification, and the resulting algorithm (MinCq) with much more experiments and information [2].

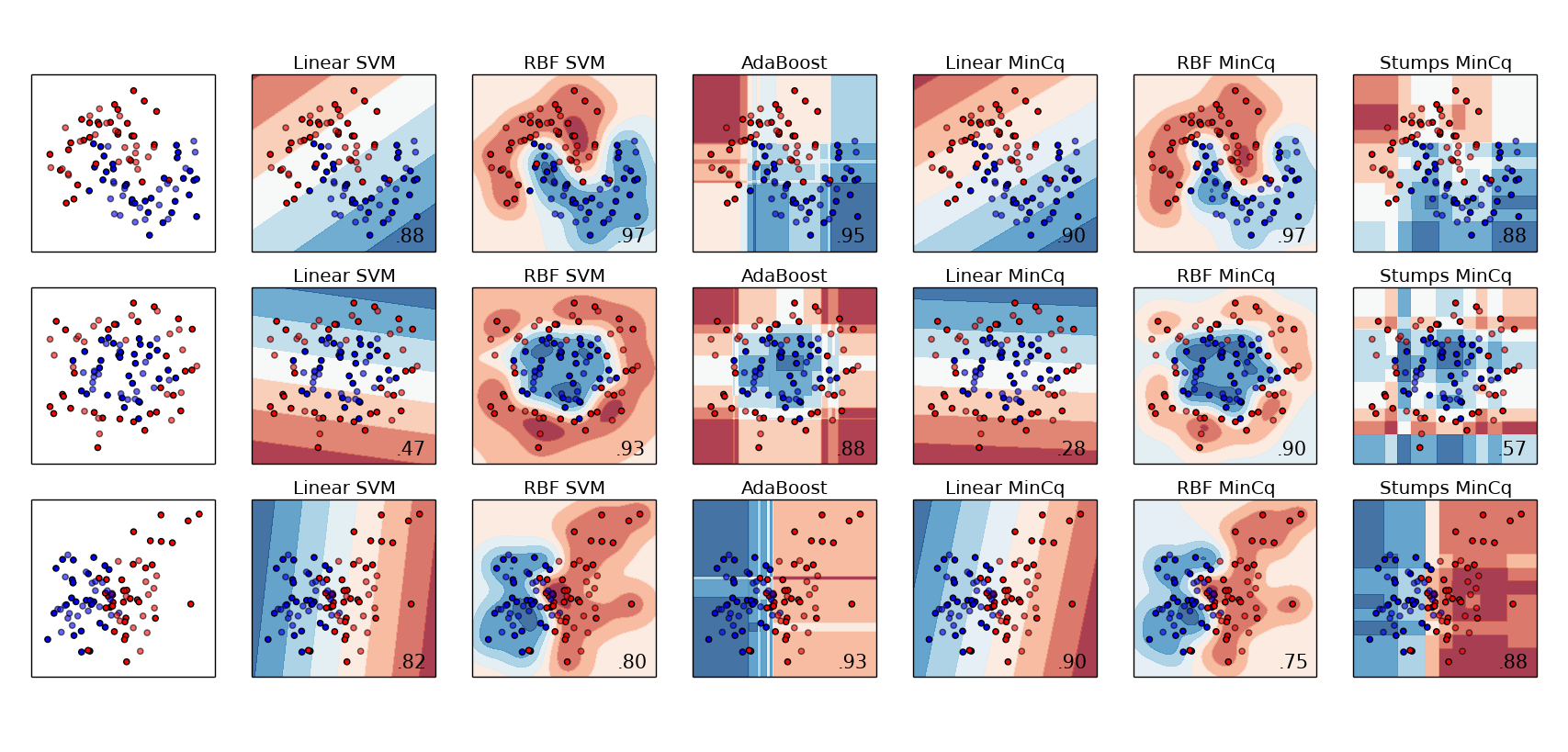
This implementation is compatible with Scikit-Learn, and comes with usage examples, one of which is based on this Scikit-Learn example

Dependencies

This Python code depends on Scikit-Learn. One example depends on Matplotlib.

Usage

$ python3 example.py

StumpsMinCq
-----------
Training set risk: 0.0357
Testing set risk: 0.0000


LinearMinCq
-----------
Training set risk: 0.2768
Testing set risk: 0.2368


PolyMinCq
-----------
Training set risk: 0.0625
Testing set risk: 0.0263


RbfMinCq
--------
Training set risk: 0.0089
Testing set risk: 0.0000

┌--------------------------------------------┐
|              RbfMinCq on Iris              |
├--------------------------------------------┤
|mu            -> |  0.0001|  0.0010|  0.0100|
|gamma            |        |        |        |
|           0.0   |  0.0357|  0.0357|  0.0357|
|           0.1   |  0.0536|  0.0357|  0.0536|
|           1.0   |  0.0536|  0.0536|  0.0536|
|          10.0   |  0.0536|  0.0536|  0.0536|
└--------------------------------------------┘

Best parameters: {'gamma': 0.0, 'mu': 0.0001}
Training set risk: 0.0179
Testing set risk: 0.0000

References

[1] François Laviolette, Mario Marchand and Jean-Francis Roy. "From PAC-Bayes Bounds to Quadratic Programs for Majority Votes". In Proceedings of the 28th International Conference on Machine Learning, 2011.

[2] Pascal Germain, Alexandre Lacasse, François Laviolette, Mario Marchand and Jean-Francis Roy. "Risk Bounds for the Majority Vote: From a PAC-Bayesian Analysis to a Learning Algorithm". Accepted for publication in the Journal of Machine Learning Research, 2014.