We read every piece of feedback, and take your input very seriously.
To see all available qualifiers, see our documentation.
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
[toc]
class Solution { public int[] getLeastNumbers(int[] arr, int k) { quickSort(arr, 0, arr.length - 1); return Arrays.copyOf(arr, k); } private void quickSort(int[] arr, int l, int r) { // 子数组长度为 1 时终止递归 if (l >= r) return; // 哨兵划分操作(以 arr[l] 作为基准数) int i = l, j = r; while (i < j) { // 右边的大于哨兵,不需要交换 while (i < j && arr[j] >= arr[l]) j--; // 左边的小于哨兵,也不需要交换 while (i < j && arr[i] <= arr[l]) i++; // 找到需要交换的值,进行交换 swap(arr, i, j); } // 将哨兵交换到分界位置 swap(arr, i, l); // 递归左(右)子数组执行哨兵划分 quickSort(arr, l, i - 1); quickSort(arr, i + 1, r); } private void swap(int[] arr, int i, int j) { int tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp; } }
class Solution{ public void quickSort(int[] a, int start, int end) { LinkedList<Integer> stack = new LinkedList<Integer>(); // 用栈模拟 if (start < end) { // 将当前的右边界入栈 stack.push(end); // 将当前的左边界入栈 stack.push(start); // 如果栈不为空,说明还有待排序的区间 while (!stack.isEmpty()) { // 后入栈的先出,第一个出栈的是左边界 int l = stack.pop(); // 后入栈的先出,第二个出栈的是右边界 int r = stack.pop(); // 内部划分完后的index int index = partition(a, l, r); // 如果当前的左边界小于index,说明左边还没有完成排序 if (l < index - 1) { // 当前的index-1是右边界 stack.push(index - 1); // 当前的左边界还是下一次划分的左边界 stack.push(l); } // 如果当前的右边界大于index,说明右边还没有完成排序 if (r > index + 1) { // 当前的右边界是下一次划分的右边界 stack.push(r); // 当前的左边界是index+1 stack.push(index + 1); } } } } // 划分数组,真正的排序逻辑 private int partition(int[] a, int l, int r) { // 选取开头的那个作为哨兵 int pivot = a[l]; int i = l, j = r; while (i < j) { // 右边的大于哨兵不需要交换 while (i < j && a[j] >= pivot) j--; // 坐标的小于哨兵不需要交换 while (i < j && a[i] <= pivot) i++; // 找到需要交换的值,进行交换 swap(a, i, j); } // 将哨兵交换到分界位置 swap(a, i, l); return i; } private void swap(int[] arr, int i, int j) { int tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp; } }
class Solution { int[] tmp; public int[] sortArray(int[] nums) { tmp = new int[nums.length]; mergeSort(nums, 0, nums.length - 1); return nums; } public void mergeSort(int[] nums, int l, int r) { if (l >= r) return; int m = (l + r) >> 1; mergeSort(nums, l, m); mergeSort(nums, m + 1, r); int i = l, j = m + 1; int cnt = 0; // 合并两个有序数组 while (i <= m && j <= r) { if (nums[i] < nums[j]) { tmp[cnt++] = nums[i++]; }else { tmp[cnt++] = nums[j++]; } } // 左边没用完 while (i <= m) tmp[cnt++] = nums[i++]; // 右边没用完 while (j <= r) tmp[cnt++] = nums[j++]; // 放到原来的数组中 for (int k = 0; k < r - l + 1; ++k) { nums[k + l] = tmp[k]; } } }
class Solution { public void heapSort(int[] nums) { int heapSize = nums.length; // 建最大堆在这里进行 buildMaxHeap(nums, heapSize); // 排序在这里进行 for (int i = heapSize - 1; i > 0; i--) { swap(nums, 0, i); heapSize--; maxHeapify(nums, 0, heapSize); } } // 建大根堆 public void buildMaxHeap(int[] nums, int heapSize) { for (int i = heapSize / 2; i >= 0; i--) { maxHeapify(nums, i, heapSize); } } public void maxHeapify(int[] nums, int index, int headSize) { // l代表左子树的元素,r代表右子树的元素,largest是当前的根节点元素的index int l = index * 2 + 1, r = index * 2 + 2, largest = index; // 如果左子树的节点大于当前的最大值,最大的是左子树的根节点的index对应的值 if (l < headSize && nums[l] > nums[largest]) largest = l; // 如果右子树的节点大于当前的最大值,最大的是右子树的根节点的index对应的值 if (r < headSize && nums[r] > nums[largest]) largest = r; // 如果最大的不是根节点的值,需要交换最大值与根节点的值,从最大值的index继续heapify if (largest != index) { swap(nums, index, largest); maxHeapify(nums, largest, headSize); } } public void swap(int[] nums, int i, int j) { int temp = nums[i]; nums[i] = nums[j]; nums[j] = temp; } }
题目描述
分别按照二叉树先序,中序和后序打印所有的节点。
示例1
输入
{1,2,3}
返回值
[[1,2,3],[2,1,3],[2,3,1]]
备注:
$n \leq 10^6$
import java.util.*; public class Solution { public int[][] threeOrders(TreeNode root) { List<Integer> pre = preOrder(root); List<Integer> in = inOrder(root); List<Integer> post = postOrder(root); int[][] res = new int[3][pre.size()]; res[0] = pre.stream().mapToInt(Integer::intValue).toArray(); res[1] = in.stream().mapToInt(Integer::intValue).toArray(); res[2] = post.stream().mapToInt(Integer::intValue).toArray(); return res; } public List preOrder(TreeNode root) { List<Integer> list = new ArrayList<>(); if (root == null) return list; Deque<TreeNode> stack = new LinkedList<>(); stack.push(root); while (!stack.isEmpty()) { TreeNode node = stack.pop(); list.add(node.val); if (node.right != null) stack.push(node.right); if (node.left != null) stack.push(node.left); } return list; } public List inOrder(TreeNode root) { List<Integer> list = new ArrayList<>(); if (root == null) return list; Deque<TreeNode> stack = new LinkedList<>(); while (root != null || !stack.isEmpty()) { while (root != null) { stack.push(root); root = root.left; } root = stack.pop(); list.add(root.val); root = root.right; } return list; } public List postOrder(TreeNode root) { LinkedList<Integer> list = new LinkedList<>(); if (root == null) return list; LinkedList<TreeNode> stack = new LinkedList<>(); stack.push(root); while (!stack.isEmpty()) { TreeNode node = stack.pop(); list.addFirst(node.val); if (node.left != null) stack.push(node.left); if (node.right != null) stack.push(node.right); } return list; } }
public class PrintABC { static Thread threadA, threadB, threadC; public static void main(String[] args) { threadA = new Thread(() -> { for (int i = 0; i < 10; i++) { // 打印当前线程名称 System.out.print(Thread.currentThread().getName()); // 唤醒下一个线程 LockSupport.unpark(threadB); // 当前线程阻塞 LockSupport.park(); } }, "A"); threadB = new Thread(() -> { for (int i = 0; i < 10; i++) { // 先阻塞等待被唤醒 LockSupport.park(); System.out.print(Thread.currentThread().getName()); // 唤醒下一个线程 LockSupport.unpark(threadC); } }, "B"); threadC = new Thread(() -> { for (int i = 0; i < 10; i++) { // 先阻塞等待被唤醒 LockSupport.park(); System.out.print(Thread.currentThread().getName()); // 唤醒下一个线程 LockSupport.unpark(threadA); } }, "C"); threadA.start(); threadB.start(); threadC.start(); } }
ABCABCABCABCABCABCABCABCABCABC Process finished with exit code 0
public class PrintABC { public static void main(String[] args) { ReentrantLock lock = new ReentrantLock(); // 使用ReentrantLock的newCondition()方法创建三个Condition // 分别对应A、B、C三个线程 Condition conditionA = lock.newCondition(); Condition conditionB = lock.newCondition(); Condition conditionC = lock.newCondition(); // A线程 new Thread(() -> { try { lock.lock(); for (int i = 0; i < 10; i++) { System.out.print(Thread.currentThread().getName()); // 叫醒B线程 conditionB.signal(); // 本线程阻塞 conditionA.await(); } // 这里有个坑,要记得在循环之后调用signal(),否则线程可能会一直处于 // wait状态,导致程序无法结束 conditionB.signal(); } catch (InterruptedException e) { e.printStackTrace(); } finally { // 在finally代码块调用unlock方法 lock.unlock(); } }, "A").start(); // B线程 new Thread(() -> { try { lock.lock(); for (int i = 0; i < 10; i++) { System.out.print(Thread.currentThread().getName()); conditionC.signal(); conditionB.await(); } conditionC.signal(); } catch (InterruptedException e) { e.printStackTrace(); } finally { lock.unlock(); } }, "B").start(); // C线程 new Thread(() -> { try { lock.lock(); for (int i = 0; i < 10; i++) { System.out.print(Thread.currentThread().getName()); conditionA.signal(); conditionC.await(); } conditionA.signal(); } catch (InterruptedException e) { e.printStackTrace(); } finally { lock.unlock(); } }, "C").start(); } }
public class PrintABC { public static void main(String[] args) { // 初始化许可数为1,A线程可以先执行 Semaphore semaphoreA = new Semaphore(1); // 初始化许可数为0,B线程阻塞 Semaphore semaphoreB = new Semaphore(0); // 初始化许可数为0,C线程阻塞 Semaphore semaphoreC = new Semaphore(0); new Thread(() -> { for (int i = 0; i < 10; i++) { try { // A线程获得许可,同时semaphoreA的许可数减为0,进入下一次循环时 // A线程会阻塞,知道其他线程执行semaphoreA.release(); semaphoreA.acquire(); // 打印当前线程名称 System.out.print(Thread.currentThread().getName()); // semaphoreB许可数加1 semaphoreB.release(); } catch (InterruptedException e) { e.printStackTrace(); } } }, "A").start(); new Thread(() -> { for (int i = 0; i < 10; i++) { try { semaphoreB.acquire(); System.out.print(Thread.currentThread().getName()); semaphoreC.release(); } catch (InterruptedException e) { e.printStackTrace(); } } }, "B").start(); new Thread(() -> { for (int i = 0; i < 10; i++) { try { semaphoreC.acquire(); System.out.print(Thread.currentThread().getName()); semaphoreA.release(); } catch (InterruptedException e) { e.printStackTrace(); } } }, "C").start(); } }
public class PrintABC { public static class Printer implements Runnable { private String name; private Object prev; private Object self; public Printer(String name, Object prev, Object self) { this.name = name; this.prev = prev; this.self = self; } @Override public void run() { int count = 10; //循环10次 while (count > 0){ //先获取prev锁 synchronized (prev) { //接着获取self锁 synchronized (self) { //打印 System.out.println(name); count--; //唤醒其他需要用到self锁的线程来竞争 //注意此时self锁还未释放 self.notify(); } //现在才释放self锁,因为需要等到临界区代码执行完毕 //立即释放prev锁,并当前线程阻塞,等待其他线程唤醒 try { prev.wait(); } catch (InterruptedException e) { e.printStackTrace(); } } } } } public static void main(String[] args) throws InterruptedException { Object a = new Object(); Object b = new Object(); Object c = new Object(); Printer pa = new Printer("A", c, a); Printer pb = new Printer("B", a, b); Printer pc = new Printer("C", b, c); new Thread(pa).start(); Thread.sleep(10);//保证初始ABC的启动顺序 new Thread(pb).start(); Thread.sleep(10); new Thread(pc).start(); Thread.sleep(10); } }
输入一个链表,反转链表后,输出新链表的表头。
{3,2,1}
解法
public class Solution { public ListNode ReverseList(ListNode head) { ListNode pre = null; ListNode cur = head; while (cur != null) { ListNode nex = cur.next; cur.next = pre; pre = cur; cur = nex; } return pre; } }
import java.util.*; public class Solution { public ListNode reverseKGroup(ListNode head, int k) { int len = 0; ListNode temp = head; // 记录链表的长度 while (temp != null) { len++; temp = temp.next; } ListNode dummyNode = new ListNode(0); dummyNode.next = head; ListNode pre = dummyNode; ListNode cur = head; for (int i = 0; i < len / k; i++) { for (int j = 0; j < k - 1; j++) { ListNode nex = cur.next; if (nex != null) { cur.next = nex.next; nex.next = pre.next; pre.next = nex; } } pre = cur; cur = cur.next; } return dummyNode.next; } }
设计LRU缓存结构,该结构在构造时确定大小,假设大小为K,并有如下两个功能
[要求]
若opt=1,接下来两个整数x, y,表示set(x, y) 若opt=2,接下来一个整数x,表示get(x),若x未出现过或已被移除,则返回-1 对于每个操作2,输出一个答案
[[1,1,1],[1,2,2],[1,3,2],[2,1],[1,4,4],[2,2]],3
[1,-1]
说明
第一次操作后:最常使用的记录为("1", 1) 第二次操作后:最常使用的记录为("2", 2),("1", 1)变为最不常用的 第三次操作后:最常使用的记录为("3", 2),("1", 1)还是最不常用的 第四次操作后:最常用的记录为("1", 1),("2", 2)变为最不常用的 第五次操作后:大小超过了3,所以移除此时最不常使用的记录("2", 2),加入记录("4", 4),并且为最常使用的记录,然后("3", 2)变为最不常使用的记录
$1 \leq K \leq N \leq 10^5$
$-2 \times 10^9 \leq x,y \leq 2 \times 10^9$
import java.util.*; public class Solution { public int[] LRU(int[][] operators, int k) { LinkedHashMap<Integer, Integer> lru = new LinkedHashMap<>(); List<Integer> list = new ArrayList<>(); for (int[] op : operators) { if (op[0] == 1) { int key = op[1]; int val = op[2]; if (lru.size() < k) { lru.put(key, val); } else { Iterator it = lru.keySet().iterator(); lru.remove(it.next()); lru.put(key, val); } } else if (op[0] == 2) { int key = op[1]; if (lru.containsKey(key)) { int val = lru.get(key); list.add(val); lru.remove(key); lru.put(key, val); } else { list.add(-1); } } } return list.stream().mapToInt(Integer::intValue).toArray(); } }
import java.util.*; public class Solution { public int[] LRU(int[][] operators, int k) { LRUCache lru = new LRUCache(k); List<Integer> list = new ArrayList<>(); for (int[] op : operators) { if (op[0] == 1) { lru.put(op[1], op[2]); } else { list.add(lru.get(op[1])); } } return list.stream().mapToInt(Integer::intValue).toArray(); } // 继承LinkedHashMap class LRUCache extends LinkedHashMap<Integer, Integer> { private int capacity; public LRUCache(int capacity) { super(capacity, 0.75f, true); this.capacity = capacity; } public int get(int key) { return super.getOrDefault(key, -1); } @Override protected boolean removeEldestEntry(Map.Entry<Integer, Integer> eldest) { return size() > capacity; } } }
请你为 最不经常使用(LFU)缓存算法设计并实现数据结构。
实现 LFUCache 类:
LFUCache
LFUCache(int capacity)
capacity
int get(int key)
void put(int key, int value)
注意「项的使用次数」就是自插入该项以来对其调用 get 和 put 函数的次数之和。使用次数会在对应项被移除后置为 0 。
get
put
为了确定最不常使用的键,可以为缓存中的每个键维护一个 使用计数器 。使用计数最小的键是最久未使用的键。
当一个键首次插入到缓存中时,它的使用计数器被设置为 1 (由于 put 操作)。对缓存中的键执行 get 或 put 操作,使用计数器的值将会递增。
1
示例:
输入: ["LFUCache", "put", "put", "get", "put", "get", "get", "put", "get", "get", "get"] [[2], [1, 1], [2, 2], [1], [3, 3], [2], [3], [4, 4], [1], [3], [4]] 输出: [null, null, null, 1, null, -1, 3, null, -1, 3, 4] 解释: // cnt(x) = 键 x 的使用计数 // cache=[] 将显示最后一次使用的顺序(最左边的元素是最近的) LFUCache lFUCache = new LFUCache(2); lFUCache.put(1, 1); // cache=[1,_], cnt(1)=1 lFUCache.put(2, 2); // cache=[2,1], cnt(2)=1, cnt(1)=1 lFUCache.get(1); // 返回 1 // cache=[1,2], cnt(2)=1, cnt(1)=2 lFUCache.put(3, 3); // 去除键 2 ,因为 cnt(2)=1 ,使用计数最小 // cache=[3,1], cnt(3)=1, cnt(1)=2 lFUCache.get(2); // 返回 -1(未找到) lFUCache.get(3); // 返回 3 // cache=[3,1], cnt(3)=2, cnt(1)=2 lFUCache.put(4, 4); // 去除键 1 ,1 和 3 的 cnt 相同,但 1 最久未使用 // cache=[4,3], cnt(4)=1, cnt(3)=2 lFUCache.get(1); // 返回 -1(未找到) lFUCache.get(3); // 返回 3 // cache=[3,4], cnt(4)=1, cnt(3)=3 lFUCache.get(4); // 返回 4 // cache=[3,4], cnt(4)=2, cnt(3)=3
提示:
0 <= capacity, key, value <= 104
105
**进阶:**你可以为这两种操作设计时间复杂度为 O(1) 的实现吗?
O(1)
解题思路
使用TreeSet保存Node的顺序,使用HashMap保存当前键值对的映射。 创建Node实现comparable接口,实现compareTo方法
class LFUCache { private Map<Integer, Node> map; private TreeSet<Node> set; private int capacity; private int time = 0; public LFUCache(int capacity) { map = new HashMap<>(); set = new TreeSet<>(); this.capacity = capacity; } public int get(int key) { if (map.containsKey(key)) { Node node = map.get(key); set.remove(node); node.cnt++; node.time = ++time; map.put(key, node); set.add(node); return node.val; } else { return -1; } } public void put(int key, int val) { if (capacity == 0) return; if (map.containsKey(key)) { Node node = map.get(key); set.remove(node); node.cnt++; node.time = ++time; node.val = val; map.put(key, node); set.add(node); } else { if (set.size() >= capacity) { Node node = set.first(); map.remove(node.key); set.remove(node); } Node node = new Node(1, ++time, key, val); map.put(key, node); set.add(node); } } private class Node implements Comparable<Node> { int cnt; int time; int key; int val; public Node(int cnt, int time, int key, int val) { this.cnt = cnt; this.time = time; this.key = key; this.val = val; } @Override public int compareTo(Node o) { return this.cnt == o.cnt ? this.time - o.time : this.cnt - o.cnt; } } } /** * Your LFUCache object will be instantiated and called as such: * LFUCache obj = new LFUCache(capacity); * int param_1 = obj.get(key); * obj.put(key,value); */
给定一个数组,找出其中最小的K个数。例如数组元素是4,5,1,6,2,7,3,8这8个数字,则最小的4个数字是1,2,3,4。如果K>数组的长度,那么返回一个空的数组
[4,5,1,6,2,7,3,8],4
[1,2,3,4]
import java.util.*; public class Solution { public ArrayList<Integer> GetLeastNumbers_Solution(int[] input, int k) { int n = input.length; if (k > n) return new ArrayList<>(); if (k == 0) return new ArrayList<>(); PriorityQueue<Integer> pq = new PriorityQueue<>((a, b) -> b - a); for (int i = 0; i < n; i++) { if (pq.size() < k) { pq.offer(input[i]); } else { if (input[i] < pq.peek()) { pq.poll(); pq.offer(input[i]); } } } ArrayList<Integer> list = new ArrayList<>(); int size = pq.size(); for (int i = 0; i < size; i++) { list.add(0, pq.poll()); } return list; } }
给出一个整数数组,请在数组中找出两个加起来等于目标值的数,
你给出的函数twoSum 需要返回这两个数字的下标(index1,index2),需要满足 index1 小于index2.。注意:下标是从1开始的
假设给出的数组中只存在唯一解
例如:
给出的数组为 {20, 70, 110, 150},目标值为90 输出 index1=1, index2=2
[3,2,4],6
[2,3]
import java.util.*; public class Solution { public int[] twoSum(int[] nums, int target) { Map<Integer, Integer> map = new HashMap<Integer, Integer>(); for (int i = 0; i < nums.length; i++) { map.put(nums[i], i); } for (int i = 0; i < nums.length; i++) { int t = target - nums[i]; if (map.containsKey(t)) { int index = map.get(t); if (index == i) continue; return index > i ? new int[]{i + 1, index + 1} : new int[]{index + 1, i + 1}; } } return new int[2]; } }
给出一个有n个元素的数组S,S中是否有元素a,b,c满足a+b+c=0?找出数组S中所有满足条件的三元组。
注意:
例如,给定的数组 S = {-10 0 10 20 -10 -40},解集为(-10, 0, 10) (-10, -10, 20)
[-2,0,1,1,2]
[[-2,0,2],[-2,1,1]]
import java.util.*; public class Solution { public ArrayList<ArrayList<Integer>> threeSum(int[] nums) { int n = nums.length; Arrays.sort(nums); ArrayList<ArrayList<Integer>> list = new ArrayList<>(); for (int i = 0; i < n - 2; i++) { // 去重复 if (i > 0 && nums[i] == nums[i - 1]) continue; int l = i + 1, r = n - 1; int f = nums[i], s = 0, t = 0; while (l < r) { s = nums[l]; t = nums[r]; if (f + s + t == 0) { // 去重复 ArrayList tList = new ArrayList(); tList.add(nums[i]); tList.add(nums[l]); tList.add(nums[r]); list.add(tList); while (l < r && nums[l] == nums[l + 1]) { l++; } while (l < r && nums[r] == nums[r - 1]) { r--; } l++; r--; } else if (f + s + t > 0) { r--; } else { l++; } } } return list; } }
给定一个数组arr,返回arr的最长无的重复子串的长度(无重复指的是所有数字都不相同)。
[2,3,4,5]
4
示例2
[2,2,3,4,3]
3
$1 \leq n \leq 10^5$
public class Solution { public int maxLength(int[] nums) { Set<Integer> set = new HashSet<>(); int n = nums.length; int l = 0, r = 0; int max = 0; while (r < n) { int val = nums[r]; if (!set.contains(val)) { set.add(val); } else { max = Math.max(set.size(), max); while (l <= r && nums[l] != val) { set.remove(nums[l]); l++; } l++; } r++; } max = Math.max(set.size(), max); return max; } }
给出一个仅包含字符'(',')','{','}','['和']',的字符串,判断给出的字符串是否是合法的括号序列 括号必须以正确的顺序关闭,"()"和"()[]{}"都是合法的括号序列,但"(]"和"([)]"不合法。
"["
false
"[]"
true
栈
如果栈为空入栈
遇到左括号就入栈
遇到右括号查看栈顶元素是不是与当前的右括号匹配,如果匹配出栈
结束时判断当前栈是否为空,为空则匹配,如果不为空,那么不匹配
import java.util.*; public class Solution { public boolean isValid(String s) { Deque<Character> stack = new LinkedList<>(); int n = s.length(); char[] arr = s.toCharArray(); for (int i = 0; i < n; i++) { char c = arr[i]; if (!stack.isEmpty()) { if ((c == ']' && stack.peek() == '[') || (c == ')' && stack.peek() == '(') || (c == '}' && stack.peek() == '{')) { stack.pop(); } else { stack.push(c); } } else { stack.push(c); } } return stack.isEmpty(); } }
请实现有重复数字的升序数组的二分查找
给定一个 元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1
[1,2,4,4,5],4
2
从左到右,查找到第1个为4的,下标为2,返回2
[1,2,4,4,5],3
-1
示例3
[1,1,1,1,1],1
0
含有重复值的二分查找的过程中,要想获得第一个数字的index,就要在找到元素后继续搜索左半部分,这样才能找到第一个(注意,如果这样做需要判断当前的左边界是不是大于了数组的长度,如果大于数组的长度,那么不存在当前的元素)
import java.util.*; public class Solution { public int search(int[] nums, int target) { return binarySearch(nums, 0, nums.length - 1, target); } public int binarySearch(int[] nums, int start, int end, int target) { int l = start, r = end, m = 0; while (l <= r) { m = l + (r - l) / 2; // 注意这里的>=是重点 if (nums[m] >= target) { r = m - 1; } else { l = m + 1; } } return l < nums.length && nums[l] == target ? l : -1; } }
对于一个字符串,请设计一个高效算法,计算其中最长回文子串的长度。
给定字符串A以及它的长度n,请返回最长回文子串的长度。
"abc1234321ab",12
7
import java.util.*; public class Solution { public int getLongestPalindrome(String S, int n) { if (S == null || S.length() == 0) return 0; boolean[][] f = new boolean[n][n]; int max = 0; // 枚举子串的长度 for (int k = 0; k < n; k++) { // 枚举子串第一个字符的位置 for (int i = 0; i < n - k; i++) { // j是子串第二个字符的位置 int j = i + k; // 如果子串的长度等于1时,那么一定是回文的(1个字符是回文的) if (k == 0) { f[i][j] = true; } else if (k == 1) { // 如果子串的长度等于2并且两个字符是相同的那么他们是回文的,否则不是回文的 f[i][j] = S.charAt(i) == S.charAt(j); } else { // 当子串的长度大于2时,如果当前两个字符相同,要看左边界右移一个字符,右边界左移动一个字符的子串是不是回文的 // 如果两个条件都满足,那么说明当前的字符是回文的 f[i][j] = S.charAt(i) == S.charAt(j) & f[i + 1][j - 1]; } // 记录回文字符的最大长度 if (f[i][j]) max = Math.max(max, k + 1); } } return max; } }
数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次,超过数组长度的一半,因此输出2。如果不存在则输出0。
[1,2,3,2,2,2,5,4,2]
摩尔投票
重新遍历一次查看当前的数字的数量是不是大于数组长度的一半
public class Solution { public int MoreThanHalfNum_Solution(int[] nums) { int most = nums[0]; int cnt = 1; int n = nums.length; for (int i = 1; i < n; i++) { if (nums[i] == most) { cnt++; } else { if (cnt > 0) { cnt--; } else { most = nums[i]; cnt = 1; } } } cnt = 0; for (int i = 0; i < n; i++) { if (nums[i] == most) { cnt++; } } if (cnt > n / 2) return most; return 0; } }
72. 编辑距离
难度困难1565
给你两个单词 word1 和 word2,请你计算出将 word1 转换成 word2 所使用的最少操作数 。
word1
word2
你可以对一个单词进行如下三种操作:
示例 1:
输入:word1 = "horse", word2 = "ros" 输出:3 解释: horse -> rorse (将 'h' 替换为 'r') rorse -> rose (删除 'r') rose -> ros (删除 'e')
示例 2:
输入:word1 = "intention", word2 = "execution" 输出:5 解释: intention -> inention (删除 't') inention -> enention (将 'i' 替换为 'e') enention -> exention (将 'n' 替换为 'x') exention -> exection (将 'n' 替换为 'c') exection -> execution (插入 'u')
0 <= word1.length, word2.length <= 500
public class EditDistancePro { public static void main(String[] args) { EditDistancePro p = new EditDistancePro(); System.out.println(p.minDistance("horse", "ros")); } public int minDistance(String word1, String word2) { int m = word1.length(); int n = word2.length(); int[][] f = new int[m + 1][n + 1]; // 当字符串2为空时,字符串1里面的所有字符都要删除 for (int i = 1; i <= m; i++) { f[i][0] = i; } // 当字符串1为空时,字符串1要插入字符串2中的每一个字符 for (int j = 1; j <= n; j++) { f[0][j] = j; } for (int i = 1; i <= m; i++) { for (int j = 1; j <= n; j++) { // 如果当前遍历的两个字符不相同 // dp[i-1][j]+1 表示第一个字符串删除第i个字符 // dp[i][j-1]+1 表示第一个字符串插入一个字符,插入的字符是第二个字符串的第j个字符 // dp[i-1][j-1]+1 表示第一个字符串中的第i-1个字符替换成第二个字符串的第j-1个字符 // 当前f[i][j]的修改次数取决于前面的子问题的最小值 if (word1.charAt(i - 1) != word2.charAt(j - 1)) { f[i][j] = Math.min(Math.min(f[i - 1][j], f[i][j - 1]), f[i - 1][j - 1]) + 1; } else { // 如果字符相同,那么不做任何操作 f[i][j] = f[i - 1][j - 1]; } } } // 输出编辑过程 int i = m, j = n; String[] op = new String[m + 1]; while (i > 0 && j > 0) { if (f[i][j] == f[i - 1][j - 1]) { op[i] = "不做变动"; i--; j--; } else if (f[i][j] == f[i - 1][j] + 1) { op[i] = "删除了一个字符\t" + word1.charAt(i); i--; } else if (f[i][j] == f[i][j - 1] + 1) { op[i] = "插入了一个字符\t" + word1.charAt(j); j--; } else if (f[i][j] == f[i - 1][j - 1] + 1) { op[i] = "替换了一个字符\t" + word1.charAt(i - 1) + "->" + word2.charAt(j - 1); i--; j--; } } for (i = 0; i < m; i++) { System.out.println(op[i]); } return f[m][n]; } }
给定一个数组arr,返回子数组的最大累加和
例如,arr = [1, -2, 3, 5, -2, 6, -1],所有子数组中,[3, 5, -2, 6]可以累加出最大的和12,所以返回12.
题目保证没有全为负数的数据
时间复杂度为O(n)O(n),空间复杂度为O(1)O(1)
[1, -2, 3, 5, -2, 6, -1]
12
$1 \leq N \leq 10^5$ $|arr_i| \leq 100$
import java.util.*; public class Solution { public int maxsumofSubarray(int[] nums) { int n = nums.length; if (n == 0) return 0; int res = nums[0]; for (int i = 1; i < n; i++) { nums[i] = Math.max(nums[i - 1] + nums[i], nums[i]); res = Math.max(nums[i], res); } return res; } }
给定两个字符串str1和str2,输出两个字符串的最长公共子序列。如果最长公共子序列为空,则输出-1。
"1A2C3D4B56","B1D23CA45B6A"
"123456"
"123456"和“12C4B6”都是最长公共子序列,任意输出一个。
$1 \leq |str_1|, |str_2| \leq 5,0001≤∣str1∣,∣str2∣≤5000$
import java.util.*; public class Solution { public String LCS(String s1, String s2) { int m = s1.length(); int n = s2.length(); int[][] dp = new int[m + 1][n + 1]; dp[0][0] = s1.charAt(0) == s2.charAt(0) ? 1 : 0; for (int i = 1; i < m; i++) { if (s1.charAt(i) == s2.charAt(0)) { dp[i][0] = 1; } else { dp[i][0] = dp[i - 1][0]; } } for (int j = 1; j < n; j++) { if (s2.charAt(j) == s1.charAt(0)) { dp[0][j] = 1; } else { dp[0][j] = dp[0][j - 1]; } } for (int i = 1; i <= m; i++) { for (int j = 1; j <= n; j++) { if (s1.charAt(i - 1) == s2.charAt(j - 1)) { dp[i][j] = dp[i - 1][j - 1] + 1; } else { // dp[i-1][j] // dp[i][j-1] dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]); } } } //反推结果 int i = m; int j = n; StringBuffer bd = new StringBuffer();//作为结果 while (i > 0 && j > 0) {//这里其实处理了i=0,j=0的,对应公式0的反推场景 if (s1.charAt(i - 1) == s2.charAt(j - 1)) { //反推公式中相等的场景 //该值一定是被选取到的,根据之前的公式,知道两条字符串的下标都前进一位 bd.append(s1.charAt(i - 1)); i--; j--; } else {//对应公式中不相等的反推场景 if (dp[i][j - 1] > dp[i - 1][j]) { //找大的那个方向,此处是左边大于上面,则该处的结果是来自左边 j--; } else if (dp[i][j - 1] < dp[i - 1][j]) { i--; } else if (dp[i][j - 1] == dp[i - 1][j]) { //对于有分支的可能时,我们选取单方向 j--; //此结果对于结果1所选取方向,str1的下标左移一位.替换为j--,则结果对应与结果2选取的方向 } } } //由于是从后往前加入字符的,需要反转才能得到正确结果 return bd.reverse().toString().length() == 0 ? "-1" : bd.toString(); } }
给定两个字符串str1和str2,输出两个字符串的最长公共子串
题目保证str1和str2的最长公共子串存在且唯一。
"1AB2345CD","12345EF"
"2345"
1 \leq |str_1|, |str_2| \leq 5\,0001≤∣str1∣,∣str2∣≤5000
import java.util.*; public class Solution { public String LCS(String str1, String str2) { int m = str1.length(), n = str2.length(); int[][] dp = new int[m + 1][n + 1]; int max = 0, index = 0; for (int i = 1; i <= m; i++) { for (int j = 1; j <= n; j++) { if (str1.charAt(i - 1) == str2.charAt(j - 1)) { dp[i][j] = dp[i - 1][j - 1] + 1; if (max < dp[i][j]) { max = dp[i][j]; index = i; } } } } return max == 0 ? "-1" : str1.substring(index - max, index); } }
给定一棵二叉树以及这棵树上的两个节点 o1 和 o2,请找到 o1 和 o2 的最近公共祖先节点。
[3,5,1,6,2,0,8,#,#,7,4],5,1
思路:
import java.util.*; public class Solution { public int lowestCommonAncestor(TreeNode root, int o1, int o2) { if (root == null) return -1; // 如果当前的值等于o1或者等于o2 那么返回当前的值 if (o1 == root.val || o2 == root.val) return root.val; int left = lowestCommonAncestor(root.left, o1, o2); int right = lowestCommonAncestor(root.right, o1, o2); // 如果左子树中不包含这两个值,一定在右子树中 if (left == -1) return right; // 如果右子树中不包含这两个值,一定在左子树中 if (right == -1) return left; // 如果这两个值分别在左子树和右子树中,那么当前的节点就是根节点,直接返回当前的值. return root.val; } }
给定一棵二叉树,已经其中没有重复值的节点,请判断该二叉树是否为搜索二叉树和完全二叉树。
{2,1,3}
[true,true]
备注: $n \leq 500000n≤500000$
判断是否是二叉搜索树:
判断是否是完全二叉树
import java.util.*; public class Solution { public boolean[] judgeIt(TreeNode root) { dfs(root); boolean flagFulll = judgeFull(root); return new boolean[]{flag, flagFulll}; } Integer pre = null; boolean flag = true; // 判断是否是二叉搜索树 public void dfs(TreeNode root) { if (root == null) return; dfs(root.left); if (pre == null) { pre = root.val; } else { if (root.val < pre) { flag = false; } pre = root.val; } dfs(root.right); } // 判断二叉树是否是完全二叉树 public boolean judgeFull(TreeNode root) { if (root == null) return true; Queue<TreeNode> queue = new LinkedList<>(); queue.offer(root); while (!queue.isEmpty()) { int size = queue.size(); for (int i = 0; i < size; i++) { TreeNode node = queue.poll(); // 如果当前节点为空,那么它后面的所有节点都应该是空的, // 如果不是空的,那么说明不是完全二叉树 if (node == null) { while (!queue.isEmpty()) { node = queue.poll(); if (node != null) return false; } // 如果后面的所有节点都是空的,那么返回true; return true; } queue.offer(node.left); queue.offer(node.right); } } return true; } }
给定一个二叉树,返回该二叉树的之字形层序遍历,(第一层从左向右,下一层从右向左,一直这样交替) 例如: 给定的二叉树是{3,9,20,#,#,15,7}, 该二叉树之字形层序遍历的结果是
[ [3], [20,9], [15,7] ]
[
[3],
[20,9],
[15,7]
]
{1,#,2}
[[1],[2]]
使用双端链表保存结果(头插和尾插)
import java.util.*; public class Solution { public ArrayList<ArrayList<Integer>> zigzagLevelOrder(TreeNode root) { ArrayList<ArrayList<Integer>> res = new ArrayList<>(); if (root == null) return res; Queue<TreeNode> queue = new LinkedList<>(); queue.offer(root); int cnt = 1; while (!queue.isEmpty()) { int size = queue.size(); LinkedList<Integer> list = new LinkedList<>(); for (int i = 0; i < size; i++) { TreeNode node = queue.poll(); if (cnt % 2 == 0) { list.addFirst(node.val); } else { list.addLast(node.val); } if (node.left != null) queue.offer(node.left); if (node.right != null) queue.offer(node.right); } res.add(new ArrayList(list)); cnt++; } return res; } }
对于一个给定的字符串,我们需要在线性(也就是O(n))的时间里对它做一些变形。首先这个字符串中包含着一些空格,就像"Hello World"一样,然后我们要做的是把着个字符串中由空格隔开的单词反序,同时反转每个字符的大小写。比如"Hello World"变形后就变成了"wORLD hELLO"。
输入描述:
给定一个字符串s以及它的长度n(1≤n≤500)
返回值描述:
请返回变形后的字符串。题目保证给定的字符串均由大小写字母和空格构成。
"This is a sample",16
"SAMPLE A IS tHIS"
使用一个StringBuilder来保存当前的单词,
import java.util.*; public class Solution { public String trans(String s, int n) { String res = ""; StringBuilder bd = new StringBuilder(); for (int i = 0; i < n; i++) { char c = s.charAt(i); if (c >= 'a' && c <= 'z') // 当前位置是小写字母转换成大写字母 bd.append(Character.toUpperCase(c)); else if (c >= 'A' && c <= 'Z') // 当前位置是大写字母转换成小写字母 bd.append(Character.toLowerCase(c)); else { // 当前位置是空格,将空格加到目前单词的前面 // 并且将当前带空格的单词加到结果前面 String temp = bd.toString(); // 将空格加到目前单词的前面 temp = c + temp; // 并且将当前带空格的单词加到结果前面 res = temp + res; // 清空当前的StringBuilder bd.delete(0, bd.length()); } } res = bd.toString() + res; return res; } }
以字符串的形式读入两个数字,编写一个函数计算它们的和,以字符串形式返回。
(字符串长度不大于100000,保证字符串仅由'0'~'9'这10种字符组成)
"1","99"
"100"
1+99=100
import java.util.*; public class Solution { public String solve(String s, String t) { int p1 = s.length() - 1, p2 = t.length() - 1; int bit = 0; StringBuilder bd = new StringBuilder(); while (p1 >= 0 && p2 >= 0) { int n1 = s.charAt(p1) - '0'; int n2 = t.charAt(p2) - '0'; int val = n1 + n2 + bit; if (val > 9) { bit = 1; val = val - 10; } else { bit = 0; } bd.append(String.valueOf(val)); p1--; p2--; } while (p1 >= 0) { int n1 = s.charAt(p1) - '0'; int val = n1 + bit; if (val > 9) { bit = 1; val = val - 10; } else { bit = 0; } bd.append(String.valueOf(val)); p1--; } while (p2 >= 0) { int n2 = t.charAt(p2) - '0'; int val = n2 + bit; if (val > 9) { bit = 1; val = val - 10; } else { bit = 0; } bd.append(String.valueOf(val)); p2--; } if (bit > 0) { bd.append(bit); } return bd.reverse().toString(); } }
对于一个给定的链表,返回环的入口节点,如果没有环,返回null
拓展:
你能给出不利用额外空间的解法么?
解题思路:
使用快慢指针,快指针一次走两步,慢指针一次走一步,如果快指针和慢指针相遇,那么从头结点再出发一个慢指针,两个慢指针再次相遇的位置即为环的入口节点。
public class Solution { public ListNode detectCycle(ListNode head) { ListNode fast = head; ListNode slow = head; while (fast != null) { fast = fast.next; if (fast != null) fast = fast.next; else return null; slow = slow.next; if (fast == slow) { ListNode t = head; while (t != slow) { t = t.next; slow = slow.next; } return t; } } return null; } }
给定一个 n * m 的矩阵 a,从左上角开始每次只能向右或者向下走,最后到达右下角的位置,路径上所有的数字累加起来就是路径和,输出所有的路径中最小的路径和。
[[1,3,5,9] ,[8,1,3,4] ,[5,0,6,1] ,[8,8,4,0]]
$1 \leq n,m \leq 2000$
$1 \leq arr_{i,j} \leq 100$
动态规划
dp[i][0] = dp[i-1][j]+matrix[i][0];
dp[0][j] = dp[i][j-1]+matrix[0][j];
dp[i][j] = Math.min(dp[i-1][j],dp[i][j-1])+matrix[i][j]
import java.util.*; public class Solution { public int minPathSum(int[][] matrix) { int m = matrix.length; int n = matrix[0].length; int[][] dp = new int[m][n]; dp[0][0] = matrix[0][0]; for (int i = 1; i < m; i++) { dp[i][0] = dp[i - 1][0] + matrix[i][0]; } for (int j = 1; j < n; j++) { dp[0][j] = dp[0][j - 1] + matrix[0][j]; } for (int i = 1; i < m; i++) { for (int j = 1; j < n; j++) { dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + matrix[i][j]; } } return dp[m - 1][n - 1]; } }
给出两个有序的整数数组 和 ,请将数组 合并到数组 中,变成一个有序的数组 注意: 可以假设 数组有足够的空间存放 数组的元素, 和 中初始的元素数目分别为 和
public class Solution { public void merge(int A[], int m, int B[], int n) { int p = m + n - 1; int p1 = m - 1; int p2 = n - 1; while (p1 >= 0 && p2 >= 0) { if (A[p1] >= B[p2]) { A[p--] = A[p1--]; } else { A[p--] = B[p2--]; } } while (p1 >= 0) { A[p--] = A[p1--]; } while (p2 >= 0) { A[p--] = B[p2--]; } } }
难度简单182
输入一个链表,输出该链表中倒数第k个节点。为了符合大多数人的习惯,本题从1开始计数,即链表的尾节点是倒数第1个节点。
例如,一个链表有 6 个节点,从头节点开始,它们的值依次是 1、2、3、4、5、6。这个链表的倒数第 3 个节点是值为 4 的节点。
6
1、2、3、4、5、6
给定一个链表: 1->2->3->4->5, 和 k = 2. 返回链表 4->5.
/** * Definition for singly-linked list. * public class ListNode { * int val; * ListNode next; * ListNode(int x) { val = x; } * } */ class Solution { public ListNode getKthFromEnd(ListNode head, int k) { ListNode fastNode = head; ListNode slowNode = head; int count = 0; while (fastNode != null) { if (count >= k) { slowNode = slowNode.next; } count++; fastNode = fastNode.next; } return slowNode; } }
给定一个链表,删除链表的倒数第 nn 个节点并返回链表的头指针 例如,
给出的链表为: 1\to 2\to 3\to 4\to 51→2→3→4→5, n= 2n=2. 删除了链表的倒数第 nn 个节点之后,链表变为1\to 2\to 3\to 51→2→3→5.
备注:
题目保证 nn 一定是有效的 请给出请给出时间复杂度为\ O(n) O(n) 的算法
{1,2},2
{2}
import java.util.*; public class Solution { public ListNode removeNthFromEnd(ListNode head, int n) { ListNode fast = head; ListNode slow = head; ListNode dummyNode = new ListNode(0); dummyNode.next = head; ListNode pre = dummyNode; int cnt = 0; while (fast != null) { fast = fast.next; if (cnt >= n) { pre = pre.next; slow = slow.next; } cnt++; } pre.next = slow.next; return dummyNode.next; } }
将两个有序的链表合并为一个新链表,要求新的链表是通过拼接两个链表的节点来生成的,且合并后新链表依然有序。
{1},{2}
{1,2}
{2},{1}
import java.util.*; public class Solution { public ListNode mergeTwoLists(ListNode l1, ListNode l2) { ListNode dummyNode = new ListNode(0); ListNode cur = dummyNode; ListNode p1 = l1; ListNode p2 = l2; while (p1 != null && p2 != null) { if (p1.val < p2.val) { cur.next = p1; p1 = p1.next; } else { cur.next = p2; p2 = p2.next; } cur = cur.next; } while (p1 != null) { cur.next = p1; p1 = p1.next; cur = cur.next; } while (p2 != null) { cur.next = p2; p2 = p2.next; cur = cur.next; } return dummyNode.next; } }
编号为 11 到 nn 的 nn 个人围成一圈。从编号为 11 的人开始报数,报到 mm 的人离开。
下一个人继续从 11 开始报数。
n-1n−1 轮结束以后,只剩下一个人,问最后留下的这个人编号是多少?
5,2
开始5个人 1,2,3,4,5 ,从1开始报数,1->1,2->2编号为2的人离开 1,3,4,5,从3开始报数,3->1,4->2编号为4的人离开 1,3,5,从5开始报数,5->1,1->2编号为1的人离开 3,5,从3开始报数,3->1,5->2编号为5的人离开 最后留下人的编号是3
1 \leq n, m \leq 100001≤n,m≤10000
import java.util.*; public class Solution { private class Node { int No; Node pre; Node next; public Node(int No, Node pre, Node next) { this.No = No; this.pre = pre; this.next = next; } } public int ysf(int n, int m) { Node head = new Node(1, null, null); Node pre = head; for (int i = 2; i <= n; i++) { pre.next = new Node(i, pre, null); pre = pre.next; } head.pre = pre; pre.next = head; int count = n; int index = 0; pre = head.pre; Node cur = head; while (cur.next != null) { index++; // 链表中去掉一个 if (index % m == 0) { // 如果链表中的元素多于一个,就删除 if (cur.next != cur) { pre.next = cur.next; cur = cur.next; } else { // 如果链表中的元素只剩下一个,即为结果,返回值 break; } } else { // 不需要处理,继续遍历 pre = cur; cur = cur.next; } } return cur.No; } }
先遍历自己的那一条链,自己的遍历完遍历另外的一条链,当两个遍历的节点相等时返回其中一个节点
/* public class ListNode { int val; ListNode next = null; ListNode(int val) { this.val = val; } }*/ public class Solution { public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) { ListNode p1 = pHead1; ListNode p2 = pHead2; while (p1 != p2) { p1 = p1 == null ? pHead2 : p1.next; p2 = p2 == null ? pHead1 : p2.next; } return p1; } }
有一个整数数组,请你根据快速排序的思路,找出数组中第K大的数。
给定一个整数数组a,同时给定它的大小n和要找的K(K在1到n之间),请返回第K大的数,保证答案存在。
[1,3,5,2,2],5,3
import java.util.*; public class Solution { public int findKth(int[] a, int n, int K) { // 注意哦,这里是n-k return quickSort(a, 0, n - 1, n - K); } public int quickSort(int[] nums, int l, int r, int k) { int i = l, j = r; int pivot = nums[l]; while (i < j) { while (i < j && nums[j] >= pivot) j--; while (i < j && nums[i] <= pivot) i++; swap(nums, i, j); } swap(nums, l, i); if (i == k) return nums[i]; else if (i < k) return quickSort(nums, i + 1, r, k); else return quickSort(nums, l, i - 1, k); } public void swap(int[] nums, int index1, int index2) { int temp = nums[index1]; nums[index1] = nums[index2]; nums[index2] = temp; } }
public class Solution { int k = 0; public ArrayList<Integer> GetLeastNumbers_Solution(int[] input, int k) { ArrayList<Integer> res = new ArrayList<>(); if (input.length < k) return res; this.k = k; quickSort(input, 0, input.length - 1); for (int i = 0; i < k; i++) { res.add(input[i]); } return res; } public void quickSort(int[] nums, int l, int r) { if (l >= r) return; int i = l, j = r; int pivot = nums[l]; while (i < j) { while (i < j && nums[j] >= pivot) j--; while (i < j && nums[i] <= pivot) i++; swap(nums, i, j); } swap(nums, l, i); if (i + 1 < k) quickSort(nums, i + 1, r); if (i + 1 > k) quickSort(nums, l, i - 1); } public void swap(int[] nums, int index1, int index2) { int temp = nums[index1]; nums[index1] = nums[index2]; nums[index2] = temp; } }
将给出的32位整数x翻转。 例1:x=123,返回321 例2:x=-123,返回-321
你有注意到翻转后的整数可能溢出吗?因为给出的是32位整数,则其数值范围为[−2^{31}, 2^{31} − 1][−231,231−1]。翻转可能会导致溢出,如果反转后的结果会溢出就返回 0。
-123
-321
import java.util.*; public class Solution { public int reverse (int x) { int res = 0; boolean neg = false; if(x<0){ neg = true; x = -x; } while(x>0){ int bit = x%10; int left = Integer.MAX_VALUE/10-bit; if(res >= left){ return 0; } res = res * 10+ bit; x = x / 10; } if(neg){ res = -res; } return res; } }
给定数组arr,设长度为n,输出arr的最长递增子序列。(如果有多个答案,请输出其中字典序最小的)
[2,1,5,3,6,4,8,9,7]
[1,3,4,8,9]
[1,2,8,6,4]
[1,2,4]
其最长递增子序列有3个,(1,2,8)、(1,2,6)、(1,2,4)其中第三个字典序最小,故答案为(1,2,4)
$n \leq 10^5$ $1 \leq arr_i \leq 10^9$
import java.util.*; public class Solution { public int[] LIS (int[] nums) { int n = nums.length; // 保存临时子序列的每个元素的index int[] indexes = new int[n]; // 保存临时的递增子序列 int[] increase = new int[n]; int incIndex = 0; increase[incIndex] = nums[0]; indexes[0] = 0; for (int i = 1; i < n; ++i) { // 如果当前的值大于最后一个元素 // 那么当前子序列的长度加1,临时递增子序列的最后一个元素是当前的元素 // 当前临时子序列的index是当前临时子序列的长度+1 if (nums[i] > increase[incIndex]) { increase[++incIndex] = nums[i]; indexes[i] = incIndex; } else { // 临时递增子序列的左边界是0,右边界是当前子序列的最后一个元素的index int left = 0, right = incIndex; // 如果当前的值小于最后一个元素,那么找到第一个比当前元素大的位置,替换那个元素为当前的元素 while (left <= right) { // 注意这里 left <= right 而不是 left < right, // 我们要替换的是第一个比 arr[i] 大的元素 int mid = (right + left) / 2; if (increase[mid] > nums[i]) { right = mid - 1; } else { left = mid + 1; } } // 用当前的元素替换已经保存的序列中第一个比当前元素大的那个元素 increase[left] = nums[i]; indexes[i] = left; } } int[] res = new int[incIndex + 1]; for (int i = indexes.length - 1; i >= 0; --i) { if (indexes[i] == incIndex) { res[incIndex--] = nums[i]; } } return res; } }
给出一组区间,请合并所有重叠的区间。
请保证合并后的区间按区间起点升序排列。
[[10,30],[20,60],[80,100],[150,180]]
[[10,60],[80,100],[150,180]]
import java.util.*; public class Solution { public ArrayList<Interval> merge(ArrayList<Interval> intervals) { Collections.sort(intervals, new Comparator<Interval>() { public int compare(Interval o1, Interval o2) { return o1.start == o2.start ? o1.end - o2.end : o1.start - o2.start; } }); ArrayList<Interval> res = new ArrayList<>(); if (intervals.size() == 0) return res; Interval last = intervals.get(0); for (int i = 0; i < intervals.size(); i++) { Interval curr = intervals.get(i); if (curr.start <= last.end) { if (res.size() > 0) res.remove(res.size() - 1); Interval temp = new Interval(last.start, Math.max(curr.end, last.end)); res.add(temp); last = temp; } else { res.add(curr); last = curr; } } return res; } }
编写一个函数来验证输入的字符串是否是有效的 IPv4 或 IPv6 地址
IPv4 地址由十进制数和点来表示,每个地址包含4个十进制数,其范围为 0 - 255, 用(".")分割。比如,172.16.254.1; 同时,IPv4 地址内的数不会以 0 开头。比如,地址 172.16.254.01 是不合法的。
IPv6 地址由8组16进制的数字来表示,每组表示 16 比特。这些组数字通过 (":")分割。比如, 2001:0db8:85a3:0000:0000:8a2e:0370:7334 是一个有效的地址。而且,我们可以加入一些以 0 开头的数字,字母可以使用大写,也可以是小写。所以, 2001:db8:85a3:0:0:8A2E:0370:7334 也是一个有效的 IPv6 address地址 (即,忽略 0 开头,忽略大小写)。
然而,我们不能因为某个组的值为 0,而使用一个空的组,以至于出现 (::) 的情况。 比如, 2001:0db8:85a3::8A2E:0370:7334 是无效的 IPv6 地址。 同时,在 IPv6 地址中,多余的 0 也是不被允许的。比如, 02001:0db8:85a3:0000:0000:8a2e:0370:7334 是无效的。
说明: 你可以认为给定的字符串里没有空格或者其他特殊字符。
"172.16.254.1"
"IPv4"
这是一个有效的 IPv4 地址, 所以返回 "IPv4"
"2001:0db8:85a3:0:0:8A2E:0370:7334"
"IPv6"
这是一个有效的 IPv6 地址, 所以返回 "IPv6"
"256.256.256.256"
"Neither"
这个地址既不是 IPv4 也不是 IPv6 地址
ip地址的类型,可能为 IPv4, IPv6, Neither
import java.util.*; public class Solution { public String solve (String IP) { return validIPAddress(IP); } public String validIPAddress(String IP) { return validIPv4(IP) ? "IPv4" : (validIPv6(IP) ? "IPv6" : "Neither"); } private boolean validIPv4(String IP) { String[] strs = IP.split("\\.", -1); if (strs.length != 4) { return false; } for (String str : strs) { if (str.length() > 1 && str.startsWith("0")) { return false; } try { int val = Integer.parseInt(str); if (!(val >= 0 && val <= 255)) { return false; } } catch (NumberFormatException numberFormatException) { return false; } } return true; } private boolean validIPv6(String IP) { String[] strs = IP.split(":", -1); if (strs.length != 8) { return false; } for (String str : strs) { if (str.length() > 4 || str.length() == 0) { return false; } try { int val = Integer.parseInt(str, 16); } catch (NumberFormatException numberFormatException) { return false; } } return true; } }
给定一个整形数组arr,已知其中所有的值都是非负的,将这个数组看作一个容器,请返回容器能装多少水。
[3,1,2,5,2,4]
5
[4,5,1,3,2]
1 \leq N \leq 10^61≤N≤106
import java.util.*; public class Solution { public long maxWater(int[] arr) { int n = arr.length; int leftMax = arr[0]; int rightMax = arr[n - 1]; int l = 0, r = n - 1; long res = 0; while (l <= r) { if (leftMax <= rightMax) { // 左边盛的水的数量由leftMax决定 leftMax = Math.max(leftMax, arr[l]); res += Math.max(leftMax - arr[l], 0); l++; } else { // 右边盛的水的数量由rightMax决定 rightMax = Math.max(rightMax, arr[r]); res += Math.max(rightMax - arr[r], 0); r--; } } return res; } }
难度困难221
请实现一个函数用来匹配包含'. '和'*'的正则表达式。模式中的字符'.'表示任意一个字符,而'*'表示它前面的字符可以出现任意次(含0次)。在本题中,匹配是指字符串的所有字符匹配整个模式。例如,字符串"aaa"与模式"a.a"和"ab*ac*a"匹配,但与"aa.a"和"ab*a"均不匹配。
'. '
'*'
'.'
"aaa"
"a.a"
"ab*ac*a"
"aa.a"
"ab*a"
示例 1:
输入: s = "aa" p = "a" 输出: false 解释: "a" 无法匹配 "aa" 整个字符串。
示例 2:
输入: s = "aa" p = "a*" 输出: true 解释: 因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此,字符串 "aa" 可被视为 'a' 重复了一次。
示例 3:
输入: s = "ab" p = ".*" 输出: true 解释: ".*" 表示可匹配零个或多个('*')任意字符('.')。
示例 4:
输入: s = "aab" p = "c*a*b" 输出: true 解释: 因为 '*' 表示零个或多个,这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。
示例 5:
输入: s = "mississippi" p = "mis*is*p*." 输出: false
s
a-z
p
.
*
注意:本题与主站 10 题相同:https://leetcode-cn.com/problems/regular-expression-matching/
class Solution { public boolean isMatch(String s, String p) { int m = s.length(); int n = p.length(); boolean[][] dp = new boolean[m + 1][n + 1]; dp[0][0] = true; for (int i = 0; i <= m; i++) { for (int j = 1; j <= n; j++) { if (p.charAt(j - 1) == '*') { dp[i][j] = dp[i][j - 2]; if (matches(s, p, i, j - 1)) { dp[i][j] = dp[i][j] || dp[i - 1][j]; } } else if (matches(s, p, i, j)) { dp[i][j] = dp[i - 1][j - 1]; } } } return dp[m][n]; } public boolean matches(String s, String p, int i, int j) { if (i == 0) return false; if (p.charAt(j - 1) == '.') return true; return s.charAt(i - 1) == p.charAt(j - 1); } }
编写一个函数来查找字符串数组中的最长公共前缀。
["abca","abc","abca","abc","abcc"]
"abc"
字典树写法
import java.util.*; public class Solution { public String longestCommonPrefix(String[] strs) { int n = strs.length; Trie tree = new Trie(); if (n == 0) return ""; if (n == 1) return strs[0]; tree.insert(strs[0]); int max = Integer.MAX_VALUE; for (int i = 1; i < n; i++) { int same = tree.search(strs[i]); max = Math.min(same, max); } return strs[0].substring(0, max); } private class Trie { Trie[] next = new Trie[26]; boolean isEnd = false; public Trie() { } public void insert(String word) { Trie root = this; char[] w = word.toCharArray(); for (int i = 0; i < w.length; i++) { int index = w[i] - 'a'; if (root.next[index] == null) root.next[index] = new Trie(); root = root.next[index]; } root.isEnd = true; } public int search(String word) { int same = 0; Trie root = this; char[] w = word.toCharArray(); for (int i = 0; i < w.length; i++) { int index = w[i] - 'a'; if (root.next[index] == null) return same; same++; root = root.next[index]; } return same; } } }
横向扫描
class Solution { public String longestCommonPrefix(String[] strs) { if (strs == null || strs.length == 0) { return ""; } String prefix = strs[0]; int count = strs.length; for (int i = 1; i < count; i++) { prefix = longestCommonPrefix(prefix, strs[i]); if (prefix.length() == 0) { break; } } return prefix; } public String longestCommonPrefix(String str1, String str2) { int length = Math.min(str1.length(), str2.length()); int index = 0; while (index < length && str1.charAt(index) == str2.charAt(index)){ index++; } return str1.substring(0, index); } } 作者:LeetCode-Solution 链接:https://leetcode-cn.com/problems/longest-common-prefix/solution/zui-chang-gong-gong-qian-zhui-by-leetcode-solution/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
给出一个升序排序的链表,删除链表中的所有重复出现的元素,只保留原链表中只出现一次的元素。 例如: 给出的链表为1 \to 2\to 3\to 3\to 4\to 4\to51→2→3→3→4→4→5, 返回1\to 2\to51→2→5. 给出的链表为1\to1 \to 1\to 2 \to 31→1→1→2→3, 返回2\to 32→3.
{1,2,2}
{1}
使用虚节点
import java.util.*; public class Solution { public ListNode deleteDuplicates(ListNode head) { ListNode dummyNode = new ListNode(0); dummyNode.next = head; ListNode pre = dummyNode; ListNode cur = head; while (cur != null) { ListNode nex = cur.next; if (nex != null && cur.val == nex.val) { while (nex != null && cur.val == nex.val) { nex = nex.next; } cur = nex; } else { pre.next = cur; pre = pre.next; cur = nex; } } pre.next = cur; return dummyNode.next; } }
题目描述 用两个栈来实现一个队列,完成队列的Push和Pop操作。 队列中的元素为int类型。
import java.util.Stack; public class Solution { Stack<Integer> stack1 = new Stack<Integer>(); Stack<Integer> stack2 = new Stack<Integer>(); public void push(int node) { stack1.push(node); } public int pop() { if(stack2.isEmpty()){ while(!stack1.isEmpty()){ stack2.push(stack1.pop()); } if(!stack2.isEmpty()){ return stack2.pop(); }else{ return -1; } }else{ return stack2.pop(); } } }
给定一个整型数组 arrarr 和一个整数 k(k>1)k(k>1)。 已知 arrarr 中只有 1 个数出现一次,其他的数都出现 kk 次。 请返回只出现了 1 次的数。
[5,4,1,1,5,1,5],3
import java.util.*; public class Solution { public int foundOnceNumber (int[] arr, int k) { int[] counts = new int[32]; for(int num : arr) { for(int j = 0; j < 32; j++) { counts[j] += num & 1; num >>>= 1; } } int res = 0; for(int i = 0; i < 32; i++) { res <<= 1; res |= counts[31 - i] % k; } return res; } }
172. 阶乘后的零
难度简单456收藏分享切换为英文接收动态反馈
给定一个整数 n,返回 n! 结果尾数中零的数量。
输入: 3 输出: 0 解释: 3! = 6, 尾数中没有零。
输入: 5 输出: 1 解释: 5! = 120, 尾数中有 1 个零.
说明: 你算法的时间复杂度应为 O(log n) 。
class Solution { public int trailingZeroes(int n) { int ans = 0; while (n > 0) { n /= 5; ans += n; } return ans; } }
给定一个表达式,其中运算符仅包含 +,-,*,/(加 减 乘 整除),可能包含括号,请你求出表达式的最终值。
+,-,*,/
import java.util.*; public class Main { public static void main(String[] args) { Scanner sc = new Scanner(System.in); String s = sc.nextLine(); // 数字栈 Deque<Integer> stack = new LinkedList<>(); // 符号栈 Deque<Character> opStack = new LinkedList<>(); // 运算的优先级 Map<Character, Integer> priority = new HashMap<>(); // 括号不参与运算优先级设置为0,没有括号时,先乘除法再加减法 priority.put('+', 1); priority.put('-', 1); priority.put('*', 2); priority.put('/', 2); priority.put('(', 0); priority.put(')', 0); int n = s.length(); for (int i = 0; i < n; i++) { char c = s.charAt(i); // 如果某个字符是数字,那么把连续的数字转换成运算数 if (Character.isDigit(c)) { int val = 0; boolean flag = false; while (i < n && Character.isDigit(s.charAt(i))) { val = val * 10 + s.charAt(i) - '0'; flag = true; i++; } if (flag) i--; // 将数字加入数字栈 stack.push(val); } else if (c == '(') {// 遇到左括号直接入栈 opStack.push(c); } else if (c == ')') {// 遇到右括号,计算括号里面的加减法,因为在下个部分没有遇到右括号之前,乘除法已经运算完了,所以这边只剩下加减法. while (opStack.peek() != '(') { eval(stack, opStack); } // 左括号出栈 opStack.pop(); } else { // 计算乘除法 // 如果符号栈不为空,并且栈顶的优先级大于目前操作符的优先级,那么对当前的符号和数字进行计算 while (!opStack.isEmpty() && priority.get(opStack.peek()) >= priority.get(c)) { // 计算的应该是乘除法 eval(stack, opStack); } // 把当前的运算符入栈(应该是加减法的符号) opStack.push(c); } } // 如果符号栈还没有空,说明还有需要计算的,此时应该只剩下加减法,直接计算即可 while (!opStack.isEmpty()) { eval(stack, opStack); } System.out.println(stack.pop()); } // 计算模块,计算模块只负责计算,不考虑优先级 public static void eval(Deque<Integer> stack, Deque<Character> opStack) { int op2 = stack.pop(); int op1 = stack.pop(); char op = opStack.pop(); int res = 0; switch (op) { case '+': res = op1 + op2; break; case '-': res = op1 - op2; break; case '*': res = op1 * op2; break; case '/': res = op1 / op2; break; } stack.push(res); } }
给定一个m x n大小的矩阵(m行,n列),按螺旋的顺序返回矩阵中的所有元素。
[[1,2,3],[4,5,6],[7,8,9]]
[1,2,3,6,9,8,7,4,5]
优雅写法
import java.util.*; public class Solution { int[][] road = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}}; int direction = 0; public ArrayList<Integer> spiralOrder(int[][] matrix) { ArrayList list = new ArrayList<>(); int m = matrix.length; if (m == 0) return list; int n = matrix[0].length; if (m * n == 0) return list; int x = 0, y = 0; int cnt = 0; boolean[][] vis = new boolean[m][n]; while (cnt < m * n) { list.add(matrix[x][y]); vis[x][y] = true; int x_ = x + road[direction][0]; int y_ = y + road[direction][1]; cnt++; if (x_ < 0 || x_ >= m || y_ < 0 || y_ >= n || vis[x_][y_]) { direction += 1; direction %= 4; } x += road[direction][0]; y += road[direction][1]; } return list; } }
剑指 Offer 49. 丑数
难度:中等
我们把只包含质因子 2、3 和 5 的数称作丑数(Ugly Number)。求按从小到大的顺序的第 n 个丑数。
示例:
输入: n = 10 输出: 12 解释: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 是前 10 个丑数。
说明:
n
注意:本题与主站 264 题相同:https://leetcode-cn.com/problems/ugly-number-ii/
public class Solution { public int GetUglyNumber_Solution(int index) { if(index==0)return 0; int[] values = new int[index+1]; int lastTwo = 0, lastThree = 0, lastFive = 0; values[0] = 1; for (int i = 1; i < index; i++) { values[i] = Math.min(Math.min(values[lastTwo] * 2, values[lastThree] * 3), values[lastFive] * 5); while (values[lastTwo] * 2 <= values[i]) lastTwo++; while (values[lastThree] * 3 <= values[i]) lastThree++; while (values[lastFive] * 5 <= values[i]) lastFive++; } return values[index - 1]; } }
难度困难405
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
输入: [7,5,6,4] 输出: 5
限制:
0 <= 数组长度 <= 50000
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/shu-zu-zhong-de-ni-xu-dui-lcof 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
归并排序
class Solution { public int reversePairs(int[] nums) { int n = nums.length; temp = new int[n]; return mergeSort(nums,0,n-1); } int [] temp ; public int mergeSort(int []nums,int l,int r){ if(l>=r)return 0; int m = l+(r-l)/2; int res= mergeSort(nums,l,m) + mergeSort(nums,m+1,r); int cnt = 0,i=l,j=m+1; while(i<=m&&j<=r){ // 如果左边的元素小于右边的元素,说明没有逆序 // 如果左边的元素大于右边的元素,说明左边的元素是逆序的 // 逆序的数量是从i到m之间的所有元素 if(nums[i]<=nums[j]){ temp[cnt++] = nums[i++]; }else{ temp[cnt++] = nums[j++]; // 一开始这里我不明白 // 从i到m之间的所有元素都是逆序的,统计从i到m之间的数字的数量 res += m - i + 1; } } // 左边的没用完 while(i<=m)temp[cnt++] = nums[i++]; // 右边的没用完 while(j<=r)temp[cnt++] = nums[j++]; // 放回原来的数组当中 for(int k=0;k<r-l+1;k++){ nums[l+k] = temp[k]; } return res; } }
实现函数 atoi 。函数的功能为将字符串转化为整数
提示:仔细思考所有可能的输入情况。这个问题没有给出输入的限制,你需要自己考虑所有可能的情况。
"123"
123
"123a4"
import java.util.*; public class Solution { public int atoi (String str) { // 处理空字符串 // 忽略前置空格 // 保存符号 // 处理非法输入 // 处理溢出 if (str == null || str.trim().length() < 1) return 0; //处理掉前后空格 char[] arr = str.trim().toCharArray(); int sign = 1, index = 0; //判断正负号 if (arr[0] == '+'){ index++; }else if (arr[0] == '-') { sign = -1; index++; } int num = 0; for (int i = index; i < arr.length; i++) { if (Character.isDigit(arr[i])) { //如果当前运算会越界的时候,直接输出结果 if(Integer.MAX_VALUE/10 - num < arr[i]-'0'){ if (sign > 0) return Integer.MAX_VALUE; else return Integer.MIN_VALUE; } // 没有溢出 num = 10 * num + arr[i] - '0'; } else //如果是字母,跳出循环,不再继续算 break; } return num * sign; } }
难度中等631
给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。
num1
num2
输入: num1 = "2", num2 = "3" 输出: "6"
输入: num1 = "123", num2 = "456" 输出: "56088"
说明:
0-9
public String multiply(String num1, String num2) { int m = num1.length(), n = num2.length(); int[] pos = new int[m + n]; for(int i = m - 1; i >= 0; i--) { for(int j = n - 1; j >= 0; j--) { int mul = (num1.charAt(i) - '0') * (num2.charAt(j) - '0'); int p1 = i + j, p2 = i + j + 1; int sum = mul + pos[p2]; pos[p1] += sum / 10; pos[p2] = (sum) % 10; } } StringBuilder sb = new StringBuilder(); for(int p : pos) if(!(sb.length() == 0 && p == 0)) sb.append(p); return sb.length() == 0 ? "0" : sb.toString(); }
给你一个非空模板串S,一个文本串T,问S在T中出现了多少次
"ababab","abababab"
"abab","abacabab"
返回值 1
空间O(n)时间O(n)的算法
import java.util.*; public class Solution { public static int kmp(String S, String T) { int[] next = getNext(S); char[] s = T.toCharArray(); char[] t = S.toCharArray(); int si = 0; int ti = 0; int ans = 0; while (si < s.length) { if (ti == -1 || s[si] == t[ti]) { si++; ti++; } else { ti = next[ti]; } if (ti == t.length) { //改造2 ans++; ti = next[ti]; } } return ans; } public static int[] getNext(String S) { char[] p = S.toCharArray(); int[] next = new int[p.length + 1]; //改造1 int j = 1; //改造1 int t = next[0] = -1; while (j <= p.length) { if (t == -1 || p[j - 1] == p[t]) { next[j++] = ++t; } else { t = next[t]; } } return next; } }
The text was updated successfully, but these errors were encountered:
No branches or pull requests
[toc]
快排
递归实现
非递归实现
归并排序
堆排序
二叉树的先序、中序、后序遍历
题目描述
分别按照二叉树先序,中序和后序打印所有的节点。
示例1
输入
返回值
备注:
多线程交替打印
LockSupport实现
Lock搭配Condition实现
Semaphore 实现
synchronized实现
反转链表
题目描述
输入一个链表,反转链表后,输出新链表的表头。
示例1
输入
返回值
解法
链表中的节点每k个一组反转
设计LRU的缓存结构
题目描述
设计LRU缓存结构,该结构在构造时确定大小,假设大小为K,并有如下两个功能
[要求]
若opt=1,接下来两个整数x, y,表示set(x, y)
若opt=2,接下来一个整数x,表示get(x),若x未出现过或已被移除,则返回-1
对于每个操作2,输出一个答案
示例1
输入
返回值
说明
备注:
继承写法
460. LFU 缓存
请你为 最不经常使用(LFU)缓存算法设计并实现数据结构。
实现
LFUCache类:LFUCache(int capacity)- 用数据结构的容量capacity初始化对象int get(int key)- 如果键存在于缓存中,则获取键的值,否则返回 -1。void put(int key, int value)- 如果键已存在,则变更其值;如果键不存在,请插入键值对。当缓存达到其容量时,则应该在插入新项之前,使最不经常使用的项无效。在此问题中,当存在平局(即两个或更多个键具有相同使用频率)时,应该去除 最近最久未使用 的键。注意「项的使用次数」就是自插入该项以来对其调用
get和put函数的次数之和。使用次数会在对应项被移除后置为 0 。为了确定最不常使用的键,可以为缓存中的每个键维护一个 使用计数器 。使用计数最小的键是最久未使用的键。
当一个键首次插入到缓存中时,它的使用计数器被设置为
1(由于 put 操作)。对缓存中的键执行get或put操作,使用计数器的值将会递增。示例:
提示:
0 <= capacity, key, value <= 104105次get和put方法**进阶:**你可以为这两种操作设计时间复杂度为
O(1)的实现吗?解题思路
使用TreeSet保存Node的顺序,使用HashMap保存当前键值对的映射。
创建Node实现comparable接口,实现compareTo方法
最小的K个数
题目描述
给定一个数组,找出其中最小的K个数。例如数组元素是4,5,1,6,2,7,3,8这8个数字,则最小的4个数字是1,2,3,4。如果K>数组的长度,那么返回一个空的数组
示例1
输入
返回值
堆(大根堆是从小到大排序,小根堆是从大到小排序)
两数之和
题目描述
给出一个整数数组,请在数组中找出两个加起来等于目标值的数,
你给出的函数twoSum 需要返回这两个数字的下标(index1,index2),需要满足 index1 小于index2.。注意:下标是从1开始的
假设给出的数组中只存在唯一解
例如:
给出的数组为 {20, 70, 110, 150},目标值为90
输出 index1=1, index2=2
示例1
输入
返回值
使用HashMap加速
三数之和
题目描述
给出一个有n个元素的数组S,S中是否有元素a,b,c满足a+b+c=0?找出数组S中所有满足条件的三元组。
注意:
示例1
输入
返回值
循环+双指针
最长无重复子串
题目描述
给定一个数组arr,返回arr的最长无的重复子串的长度(无重复指的是所有数字都不相同)。
示例1
输入
返回值
示例2
输入
返回值
备注:
滑动窗口+集合检测是否重复
括号序列
题目描述
给出一个仅包含字符'(',')','{','}','['和']',的字符串,判断给出的字符串是否是合法的括号序列
括号必须以正确的顺序关闭,"()"和"()[]{}"都是合法的括号序列,但"(]"和"([)]"不合法。
示例1
输入
返回值
示例2
输入
返回值
栈
如果栈为空入栈
遇到左括号就入栈
遇到右括号查看栈顶元素是不是与当前的右括号匹配,如果匹配出栈
结束时判断当前栈是否为空,为空则匹配,如果不为空,那么不匹配
含有重复元素的二分查找
题目描述
请实现有重复数字的升序数组的二分查找
给定一个 元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1
示例1
输入
返回值
说明
示例2
输入
返回值
示例3
输入
返回值
含有重复值的二分查找的过程中,要想获得第一个数字的index,就要在找到元素后继续搜索左半部分,这样才能找到第一个(注意,如果这样做需要判断当前的左边界是不是大于了数组的长度,如果大于数组的长度,那么不存在当前的元素)
最长回文子串
题目描述
对于一个字符串,请设计一个高效算法,计算其中最长回文子串的长度。
给定字符串A以及它的长度n,请返回最长回文子串的长度。
示例1
输入
返回值
动态规划
数组中出现次数超过一半的数字
题目描述
数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次,超过数组长度的一半,因此输出2。如果不存在则输出0。
示例1
输入
返回值
摩尔投票
重新遍历一次查看当前的数字的数量是不是大于数组长度的一半
编辑距离(记录编辑过程)
72. 编辑距离
难度困难1565
给你两个单词
word1和word2,请你计算出将word1转换成word2所使用的最少操作数 。你可以对一个单词进行如下三种操作:
示例 1:
示例 2:
提示:
0 <= word1.length, word2.length <= 500word1和word2由小写英文字母组成子数组最大累加和
题目描述
给定一个数组arr,返回子数组的最大累加和
例如,arr = [1, -2, 3, 5, -2, 6, -1],所有子数组中,[3, 5, -2, 6]可以累加出最大的和12,所以返回12.
题目保证没有全为负数的数据
[要求]
时间复杂度为O(n)O(n),空间复杂度为O(1)O(1)
示例1
输入
返回值
备注:
最长公共子序列(返回序列)
题目描述
给定两个字符串str1和str2,输出两个字符串的最长公共子序列。如果最长公共子序列为空,则输出-1。
示例1
输入
返回值
说明
备注:
最长公共子串
题目描述
给定两个字符串str1和str2,输出两个字符串的最长公共子串
题目保证str1和str2的最长公共子串存在且唯一。
示例1
输入
返回值
备注:
二叉树的最近公共祖先
题目描述
给定一棵二叉树以及这棵树上的两个节点 o1 和 o2,请找到 o1 和 o2 的最近公共祖先节点。
示例1
输入
返回值
递归
思路:
判断一颗二叉树是否为二叉搜索树和完全二叉树
题目描述
给定一棵二叉树,已经其中没有重复值的节点,请判断该二叉树是否为搜索二叉树和完全二叉树。
示例1
输入
{2,1,3}返回值
[true,true]备注:
$n \leq 500000n≤500000$
判断是否是二叉搜索树:
判断是否是完全二叉树
二叉树的之字形层序遍历
给定一个二叉树,返回该二叉树的之字形层序遍历,(第一层从左向右,下一层从右向左,一直这样交替)
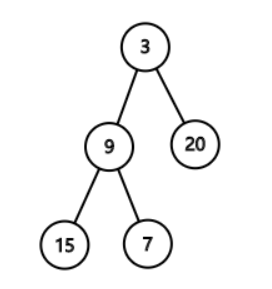
例如:
给定的二叉树是{3,9,20,#,#,15,7},
该二叉树之字形层序遍历的结果是
示例1
输入
返回值
使用双端链表保存结果(头插和尾插)
字符串变形
题目描述
对于一个给定的字符串,我们需要在线性(也就是O(n))的时间里对它做一些变形。首先这个字符串中包含着一些空格,就像"Hello World"一样,然后我们要做的是把着个字符串中由空格隔开的单词反序,同时反转每个字符的大小写。比如"Hello World"变形后就变成了"wORLD hELLO"。
输入描述:
给定一个字符串s以及它的长度n(1≤n≤500)
返回值描述:
请返回变形后的字符串。题目保证给定的字符串均由大小写字母和空格构成。
示例1
输入
"This is a sample",16返回值
"SAMPLE A IS tHIS"使用一个StringBuilder来保存当前的单词,
大数加法
题目描述
以字符串的形式读入两个数字,编写一个函数计算它们的和,以字符串形式返回。
(字符串长度不大于100000,保证字符串仅由'0'~'9'这10种字符组成)
示例1
输入
返回值
说明
链表中环的入口点
题目描述
对于一个给定的链表,返回环的入口节点,如果没有环,返回null
拓展:
你能给出不利用额外空间的解法么?
解题思路:
使用快慢指针,快指针一次走两步,慢指针一次走一步,如果快指针和慢指针相遇,那么从头结点再出发一个慢指针,两个慢指针再次相遇的位置即为环的入口节点。
矩阵的最小路径和
题目描述
给定一个 n * m 的矩阵 a,从左上角开始每次只能向右或者向下走,最后到达右下角的位置,路径上所有的数字累加起来就是路径和,输出所有的路径中最小的路径和。
示例1
输入
返回值
备注:
动态规划
dp[i][0] = dp[i-1][j]+matrix[i][0];dp[0][j] = dp[i][j-1]+matrix[0][j];dp[i][j] = Math.min(dp[i-1][j],dp[i][j-1])+matrix[i][j]合并有序数组
题目描述
给出两个有序的整数数组 和
和  ,请将数组
,请将数组  合并到数组
合并到数组  中,变成一个有序的数组
中,变成一个有序的数组 数组有足够的空间存放
数组有足够的空间存放  数组的元素,
数组的元素,  和
和  中初始的元素数目分别为
中初始的元素数目分别为  和
和 
注意:
可以假设
链表中的倒数第k个节点
剑指 Offer 22. 链表中倒数第k个节点
难度简单182
输入一个链表,输出该链表中倒数第k个节点。为了符合大多数人的习惯,本题从1开始计数,即链表的尾节点是倒数第1个节点。
例如,一个链表有
6个节点,从头节点开始,它们的值依次是1、2、3、4、5、6。这个链表的倒数第3个节点是值为4的节点。示例:
删除链表的倒数第n个节点
题目描述
给定一个链表,删除链表的倒数第 nn 个节点并返回链表的头指针
例如,
给出的链表为: 1\to 2\to 3\to 4\to 51→2→3→4→5, n= 2n=2.
删除了链表的倒数第 nn 个节点之后,链表变为1\to 2\to 3\to 51→2→3→5.
备注:
题目保证 nn 一定是有效的
请给出请给出时间复杂度为\ O(n) O(n) 的算法
示例1
输入
返回值
合并两个有序链表
题目描述
将两个有序的链表合并为一个新链表,要求新的链表是通过拼接两个链表的节点来生成的,且合并后新链表依然有序。
示例1
输入
返回值
示例2
输入
返回值
环形链表的约瑟夫问题
题目描述
编号为 11 到 nn 的 nn 个人围成一圈。从编号为 11 的人开始报数,报到 mm 的人离开。
下一个人继续从 11 开始报数。
n-1n−1 轮结束以后,只剩下一个人,问最后留下的这个人编号是多少?
示例1
输入
返回值
说明
备注:
两个链表的第一个公共节点
先遍历自己的那一条链,自己的遍历完遍历另外的一条链,当两个遍历的节点相等时返回其中一个节点
第K大的数
题目描述
有一个整数数组,请你根据快速排序的思路,找出数组中第K大的数。
给定一个整数数组a,同时给定它的大小n和要找的K(K在1到n之间),请返回第K大的数,保证答案存在。
示例1
输入
返回值
最小的k个数(k个数之间不要求顺序)
给定一个数组,找出其中最小的K个数。例如数组元素是4,5,1,6,2,7,3,8这8个数字,则最小的4个数字是1,2,3,4。如果K>数组的长度,那么返回一个空的数组
示例1
输入
返回值
最小的k个数(k个数之间要求顺序时最好用堆)
反转数字
题目描述
将给出的32位整数x翻转。
例1:x=123,返回321
例2:x=-123,返回-321
你有注意到翻转后的整数可能溢出吗?因为给出的是32位整数,则其数值范围为[−2^{31}, 2^{31} − 1][−231,231−1]。翻转可能会导致溢出,如果反转后的结果会溢出就返回 0。
示例1
输入
返回值
最长递增子序列
题目描述
给定数组arr,设长度为n,输出arr的最长递增子序列。(如果有多个答案,请输出其中字典序最小的)
示例1
输入
返回值
示例2
输入
返回值
说明
备注:
合并区间
题目描述
给出一组区间,请合并所有重叠的区间。
请保证合并后的区间按区间起点升序排列。
示例1
输入
返回值
验证IP地址
题目描述
编写一个函数来验证输入的字符串是否是有效的 IPv4 或 IPv6 地址
IPv4 地址由十进制数和点来表示,每个地址包含4个十进制数,其范围为 0 - 255, 用(".")分割。比如,172.16.254.1;
同时,IPv4 地址内的数不会以 0 开头。比如,地址 172.16.254.01 是不合法的。
IPv6 地址由8组16进制的数字来表示,每组表示 16 比特。这些组数字通过 (":")分割。比如, 2001:0db8:85a3:0000:0000:8a2e:0370:7334 是一个有效的地址。而且,我们可以加入一些以 0 开头的数字,字母可以使用大写,也可以是小写。所以, 2001:db8:85a3:0:0:8A2E:0370:7334 也是一个有效的 IPv6 address地址 (即,忽略 0 开头,忽略大小写)。
然而,我们不能因为某个组的值为 0,而使用一个空的组,以至于出现 (::) 的情况。 比如, 2001:0db8:85a3::8A2E:0370:7334 是无效的 IPv6 地址。
同时,在 IPv6 地址中,多余的 0 也是不被允许的。比如, 02001:0db8:85a3:0000:0000:8a2e:0370:7334 是无效的。
说明: 你可以认为给定的字符串里没有空格或者其他特殊字符。
示例1
输入
返回值
说明
示例2
输入
返回值
说明
示例3
输入
返回值
说明
备注:
接雨水问题
题目描述
给定一个整形数组arr,已知其中所有的值都是非负的,将这个数组看作一个容器,请返回容器能装多少水。
示例1
输入
返回值
示例2
输入
返回值
备注:
正则表达式匹配
剑指 Offer 19. 正则表达式匹配
难度困难221
请实现一个函数用来匹配包含
'. '和'*'的正则表达式。模式中的字符'.'表示任意一个字符,而'*'表示它前面的字符可以出现任意次(含0次)。在本题中,匹配是指字符串的所有字符匹配整个模式。例如,字符串"aaa"与模式"a.a"和"ab*ac*a"匹配,但与"aa.a"和"ab*a"均不匹配。示例 1:
示例 2:
示例 3:
示例 4:
示例 5:
s可能为空,且只包含从a-z的小写字母。p可能为空,且只包含从a-z的小写字母以及字符.和*,无连续的'*'。注意:本题与主站 10 题相同:https://leetcode-cn.com/problems/regular-expression-matching/
最长公共前缀
题目描述
编写一个函数来查找字符串数组中的最长公共前缀。
示例1
输入
返回值
字典树写法
横向扫描
删除链表中重复出现的元素
题目描述
给出一个升序排序的链表,删除链表中的所有重复出现的元素,只保留原链表中只出现一次的元素。
例如:
给出的链表为1 \to 2\to 3\to 3\to 4\to 4\to51→2→3→3→4→4→5, 返回1\to 2\to51→2→5.
给出的链表为1\to1 \to 1\to 2 \to 31→1→1→2→3, 返回2\to 32→3.
示例1
输入
返回值
使用虚节点
两个栈实现队列
题目描述
用两个栈来实现一个队列,完成队列的Push和Pop操作。 队列中的元素为int类型。
数组中只出现一次的数字(其余都出现了k次)
题目描述
给定一个整型数组 arrarr 和一个整数 k(k>1)k(k>1)。
已知 arrarr 中只有 1 个数出现一次,其他的数都出现 kk 次。
请返回只出现了 1 次的数。
示例1
输入
返回值
阶乘后的0
172. 阶乘后的零
难度简单456收藏分享切换为英文接收动态反馈
给定一个整数 n,返回 n! 结果尾数中零的数量。
示例 1:
示例 2:
说明: 你算法的时间复杂度应为 O(log n) 。
表达式求值
给定一个表达式,其中运算符仅包含
+,-,*,/(加 减 乘 整除),可能包含括号,请你求出表达式的最终值。螺旋矩阵
题目描述
给定一个m x n大小的矩阵(m行,n列),按螺旋的顺序返回矩阵中的所有元素。
示例1
输入
返回值
优雅写法
生成丑数
剑指 Offer 49. 丑数
难度:中等
我们把只包含质因子 2、3 和 5 的数称作丑数(Ugly Number)。求按从小到大的顺序的第 n 个丑数。
示例:
说明:
1是丑数。n不超过1690。注意:本题与主站 264 题相同:https://leetcode-cn.com/problems/ugly-number-ii/
剑指 Offer 51. 数组中的逆序对
难度困难405
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
示例 1:
限制:
归并排序
字符串转化为数字
实现函数 atoi 。函数的功能为将字符串转化为整数
提示:仔细思考所有可能的输入情况。这个问题没有给出输入的限制,你需要自己考虑所有可能的情况。
示例1
输入
返回值
输入
返回值
43. 字符串相乘(大数乘法)
难度中等631
给定两个以字符串形式表示的非负整数
num1和num2,返回num1和num2的乘积,它们的乘积也表示为字符串形式。示例 1:
示例 2:
说明:
num1和num2的长度小于110。num1和num2只包含数字0-9。num1和num2均不以零开头,除非是数字 0 本身。优雅写法
KMP算法
题目描述
给你一个非空模板串S,一个文本串T,问S在T中出现了多少次
示例1
输入
"ababab","abababab"返回值
2示例2
输入
"abab","abacabab"返回值
1备注:
The text was updated successfully, but these errors were encountered: