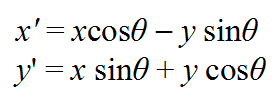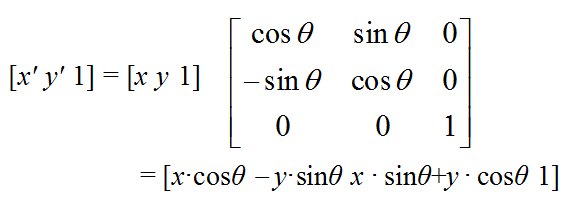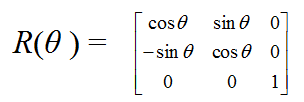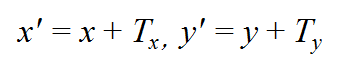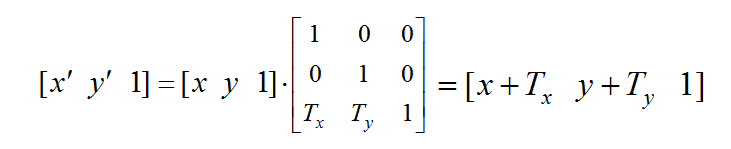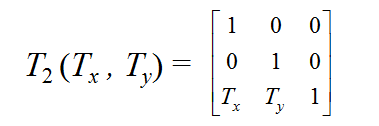---

Android动画总结之有赞、邮箱大师进度条实现原理

原文地址

相关文章 基于贝塞尔曲线的安卓动画插值器

一、效果

二、有赞加载进度条

四个正方形的运动可以分解成两个分运动，一个是平移运动，一个是自身的旋转运动。在实现这个动画上有两个思路：

• 一个是通过Android提供的Animation或者Animator操作视图，让一个正方形的视图在translate动画的同时进行rotate动画，只需要设置rotate动画的pivot坐标为视图的中心点就可以了。
• 另一个是直接在canvas上绘制正方形，通过canvas的坐标变换实现动画。

下面主要说第二种方式的原理：

• 平移：平移canvas，在平行与手机屏幕的平面坐标系中，水平向右方向为X轴，竖直向下方向为Y轴，把原点平移到视图的中心点，只需要在水平和竖直的正方向平移就可以了。

canvas.translate(mBounds.width() / 2, mBounds.height() / 2);

• 旋转：想要完成一个矩形围绕其中心点顺时针旋转一个角度，首先要意识到旋转的过程中，只改变了坐标系的方向并没有改变坐标系的原点位置。换句话说，如果你需要围绕坐标系原点做旋转，那么你只需要旋转操作，如果你需要围绕除了原点以外的另外一个点（比如当前现在正方形的中心点），那么你需要先做平移操作，先把坐标系平移到一个正确的点在做旋转操作。如图所示：

canvas.translate((float) (x + (1 - 1.414f * Math.sin((45 - degree) / 180f * Math.PI)) * halfLength),(float) (y - (1.414f * Math.cos((45 - degree) / 180f * Math.PI) - 1) * halfLength));
canvas.rotate(degree);
drawable.draw(canvas);

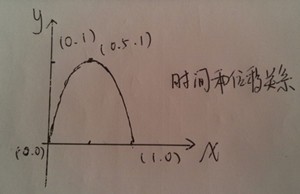
• 动画插值：可以看到，每个正方形的平移运动周期是从起始点回到起始点，在时间的中点上达到平移的最大值。反应在平面坐标中的情况就是，一条通过(0, 0), (0.5, 1),(1, 0)三点，在(0.5, 1)达到最大值的一元二次方程。可以间接得到这个插值器是：

// 过（0,0），（0.5,1），（1,0）的一元二次方程
Interpolator mInterpolator = new Interpolator() {
    @Override
    public float getInterpolation(float input) {
        return -4 * input * input + 4 * input;
    }
};

三、网易邮箱大师加载进度条

圆弧的动画需要分解成四个分动画：

• 画笔宽度变化：绘制圆弧的画笔宽度在动画
• 圆弧长度变化：绘制圆弧的长度在动画
• 旋转变化：绘制每段圆弧的起点在动画
• 圆弧半径变化：绘制圆弧的半径在动画

public ObjectAnimator[] getAtomAnimator(Atom atom, Rect bound) {
    ObjectAnimator[] result = new ObjectAnimator[4];
    result[0] = ObjectAnimator.ofFloat(atom, "delta", 4f, 9f);
    result[0].setInterpolator(mPaintInterpolator);
    switch (atom.getId()) {
        case 0:
            result[1] = ObjectAnimator.ofInt(atom, "rotate", 0, 360);
            break;
        case 1:
            result[1] = ObjectAnimator.ofInt(atom, "rotate", 120, 480);
            break;
        case 2:
            result[1] = ObjectAnimator.ofInt(atom, "rotate", 240, 600);
            break;
        default:
            throw new RuntimeException();
    }
    result[1].setInterpolator(mRotateInterpolator);
    result[2] = ObjectAnimator.ofFloat(atom, "length", 80f, 59f);
    result[2].setInterpolator(mPaintInterpolator);
    result[3] = ObjectAnimator.ofFloat(atom, "r", 0, mScaleFactor * getIntrinsicWidth());
    result[3].setInterpolator(mPaintInterpolator);
    return result;
}

四、Canvas图形变换原理

2.1、平移

设图形上点P(x, y)，在x轴和y轴方向分别移动Tx和Ty，结果生成新的点P'(x', y')，则:

用矩阵形式可表示为: 平移变换矩阵为：

2.2、缩放

设图形上的点P(x, y)在x轴和y轴方向分别作Sx倍和Sy倍的缩放，结果生成新的点坐标P'(x', y')，则: 用矩阵表示为： 比例变换矩阵为：

2.3、旋转

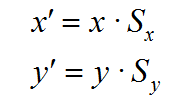
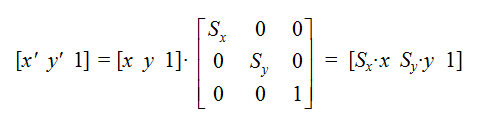
设点P(x, y)绕原点旋转变换θ角度(假设按逆时针旋转为正角)，生成的新的点坐标P'(x', y')，则： 用矩阵表示为： 旋转变换矩阵为：