The ADCME library (Automatic Differentiation Library for Computational and Mathematical Engineering) aims at general and scalable inverse modeling in scientific computing with gradient-based optimization techniques. It is built on the deep learning framework, graph-mode TensorFlow, which provides the automatic differentiation and parallel computing backend. The dataflow model adopted by the framework makes it suitable for high performance computing and inverse modeling in scientific computing. The design principles and methodologies are summarized in the slides.

Several features of the library are

• MATLAB-style Syntax. Write A*B for matrix production instead of tf.matmul(A,B).
• Custom Operators. Implement operators in C/C++ for performance critical parts; incorporate legacy code or specially designed C/C++ code in ADCME; automatic differentiation through implicit schemes and iterative solvers.
• Numerical Scheme. Easy to implement numerical schemes for solving PDEs.
• Physics Constrained Learning. Embed neural network into PDEs and solve with any numerical schemes, including implicit and iterative schemes.
• Static Graphs. Compilation time computational graph optimization; automatic parallelism for your simulation codes.
• Parallel Computing. Concurrent execution and model/data parallel distributed optimization.
• Custom Optimizers. Large scale constrained optimization? Use CustomOptimizer to integrate your favorite optimizer. Try out prebuilt Ipopt and NLopt optimizers.
• Sparse Linear Algebra. Sparse linear algebra library tailored for scientific computing.
• Inverse Modeling. Many inverse modeling algorithms have been developed and implemented in ADCME, with wide applications in solid mechanics, fluid dynamics, geophysics, and stochastic processes.

Start building your forward and inverse modeling using ADCME today!

Documentation	Tutorial	Applications

Why graph mode TensorFlow?

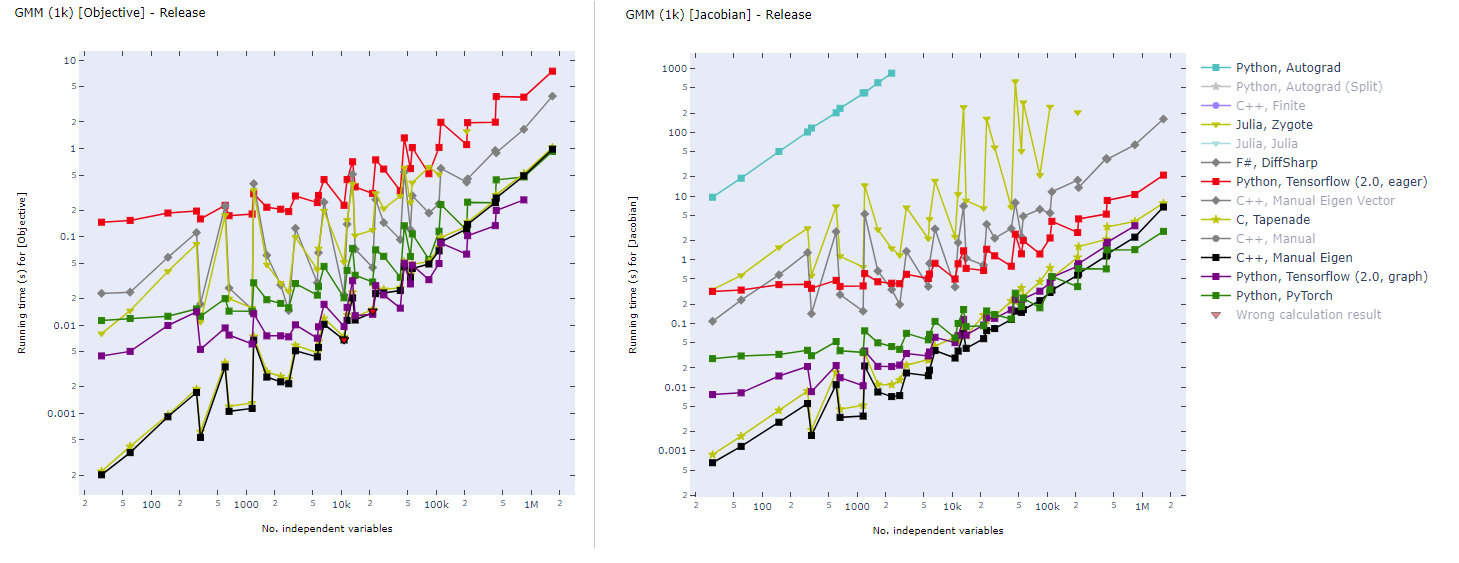
Static computational graph enables compilation time optimization. Below is a benchmark of common AD software from here. In inverse modeling, we usually have a scalar-valued objective function, so the left panel is most relevant for ADCME.

Installation

1. Install Julia

2. Install ADCME

julia> ]
pkg> add ADCME

3. (Optional) Test ADCME.jl

julia> ]
pkg> test ADCME

See Troubleshooting if you encounter any compilation problems.

4. (Optional) Enable GPU Support To enable GPU support, first, make sure nvcc is available from your environment (e.g., type nvcc in your shell and you should get the location of the executable binary file).

ENV["GPU"] = 1
Pkg.build("ADCME")

For manual installation without access to the internet, see here.

⚠️ PyCall is forced to use the default interpreter by ADCME. Do not try to reset the interpreter by rebuilding PyCall.

Tutorial

Here we present two inverse problem examples. The first one is a parameter estimation problem, and the second one is a function inverse problem.

Parameter Inverse Problem

Consider solving the following problem

where

Assume that we have observed u(0.5)=1, we want to estimate b. In this case, he true value should be b=1.

using LinearAlgebra
using ADCME

n = 101 # number of grid nodes in [0,1]
h = 1/(n-1)
x = LinRange(0,1,n)[2:end-1]

b = Variable(10.0) # we use Variable keyword to mark the unknowns
A = diagm(0=>2/h^2*ones(n-2), -1=>-1/h^2*ones(n-3), 1=>-1/h^2*ones(n-3)) 
B = b*A + I  # I stands for the identity matrix
f = @. 4*(2 + x - x^2) 
u = B\f # solve the equation using built-in linear solver
ue = u[div(n+1,2)] # extract values at x=0.5

loss = (ue-1.0)^2 

# Optimization
sess = Session(); init(sess) 
BFGS!(sess, loss)

println("Estimated b = ", run(sess, b))

Expected output

Estimated b = 0.9995582304494237

The gradients can be obtained very easily. For example, if we want the gradients of loss with respect to b, the following code will create a Tensor for the gradient

julia> gradients(loss, b)
PyObject <tf.Tensor 'gradients_1/Mul_grad/Reshape:0' shape=() dtype=float64>

Function Inverse Problem

Consider a nonlinear PDE,

where

Here f(x) can be computed from an analytical solution

In this problem, we are given the values of u(x) on the grid points and want to estimate the nonparametric function b(u). We approximate b(u) using a neural network and use the residual minimization method to find the optimal weights and biases of the neural network. The minimization problem is given by

using LinearAlgebra
using ADCME
using PyPlot

n = 101 
h = 1/(n-1)
x = LinRange(0,1,n)|>collect

u = sin.(π*x)
f = @. (1+u^2)/(1+2u^2) * π^2 * u + u 
b = squeeze(ae(u[2:end-1], [20,20,1])) 

residual = -b.*(u[3:end]+u[1:end-2]-2u[2:end-1])/h^2 + u[2:end-1] - f[2:end-1]
loss = sum(residual^2)

sess = Session(); init(sess)
BFGS!(sess, loss)

plot(x, (@. (1+x^2)/(1+2*x^2)), label="Reference")
plot(u[2:end-1], run(sess, b), "o", markersize=5., label="Estimated")
legend(); xlabel("\$u\$"); ylabel("\$b(u)\$"); grid("on")

Here we show the estimated coefficient function and the reference one:

See Applications for more inverse modeling techniques and examples.

Under the Hood: Computational Graph

Under the hood, a static computational graph is automatic constructed. The computational graph guides the runtime execution and provides dependencies of data flows for automatic differentiation. Here we show the computational graph in the parameter inverse problem:

See a detailed tutorial, or a full documentation.

Featured Applications

Constitutive Modeling	Seismic Inversion	Coupled Two-Phase Flow and Time-lapse FWI	Calibrating Jump Diffusion

Domain specific software based on ADCME

ADSeismic.jl: Inverse Problems in Earthquake Location/Source-Time Function, FWI, Rupture Process

FwiFlow.jl: Seismic Inversion, Two-phase Flow, Coupled seismic and flow equations

NNFEM.jl: Constitutive Modeling, Elasticity, Plasticity, Hyperelasticity, Finite Element Method on Unstructured Grid

LICENSE

ADCME.jl is released under MIT License. See License for details.