-
-
Notifications
You must be signed in to change notification settings - Fork 5.5k
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Resolves #47565 and #36534. nthroot() for complex variables implemented. #47860
base: master
Are you sure you want to change the base?
Conversation
…ang#47565. One minor fix needed.
|
This seems potentially possible to do as an iterator to avoid the allocations? |
|
@bramtayl Is this what you asked for? diff --git a/base/complex.jl b/base/complex.jl
index 27fc62dfff..67e9721126 100644
--- a/base/complex.jl
+++ b/base/complex.jl
@@ -561,7 +561,7 @@ end
# return Complex(abs(iz)/r/2, copysign(r,iz))
# end
-function nthroot(z::Complex, n::Int)
+function nthroot(z::Complex, n::Integer)
z = float(z)
x, y = reim(z)
if x==y==0
@@ -569,9 +569,9 @@ function nthroot(z::Complex, n::Int)
end
r = abs(z)
θ = angle(z)
- roots = Array{Complex}(undef, n)
+ roots = ComplexF64[]
for k in 1:n
- roots[k] = r^(1/n)*(cos((θ+2*pi*(k-1))/n) + sin((θ+2*pi*(k-1))/n)im)
+ push!(roots, ComplexF64(r^(1/n)*(cis((θ+2*pi*(k-1))/n))))
end
return roots
end |
|
Not quite. I was thinking something more along the lines of |
…ented for complex and real numbers.
@bramtayl Give me some time to look into it. Rest is my function correct mathematically? |
|
I like returning a Even when returning all roots, there is a question about where to put the branch point. Where does this PR put it? i.e. for which As an aside you can post code like this julia> sqrt(2)
1.4142135623730951which is better for folks with weak internet connections, renders the same way no matter who is posting it (unlike screenshots which depend on the editor settings of the person posting them) and more importantly, can be copied. |
I think now I am getting the rough idea of what is required here. Lemme refer the Docs |
|
This example might be helpful: |
|
@LilithHafner @bramtayl struct RootsVector{T<:Complex} <: AbstractVector{T}
z::T
n::Int
end
Base.size(S::RootsVector) = S.n
Base.IndexStyle(S::RootsVector) = IndexLinear()
Base.getindex(S::RootsVector, i::Int) = abs(S.z)^(1/S.n)*(Float16(cos((angle(S.z)+2*pi*(i-1))/S.n)) + Float16(sin((angle(S.z)+2*pi*(i-1))/S.n))im)But I am unable to figure out two things:-
julia> roots = RootsVector(1+0im, 3)
ERROR: UndefVarError: `RootsVector` not defined
Stacktrace:
[1] top-level scope
@ REPL[1]:1
julia> roots = Base.RootsVector(1+0im, 3)
1×1×1 Base.RootsVector{Complex{Int64}} with indices 1×2×3:
Error showing value of type Base.RootsVector{Complex{Int64}}:
ERROR: MethodError: no method matching unitrange(::Int64)
julia> for i in 1:3
println(roots[i])
end
1.0 + 0.0im
-0.5 + 0.8662109375im
-0.5 - 0.8662109375imSample Example that it is returning correct values julia> roots = Base.RootsVector(1+0im, 4)
1×1×1×1 Base.RootsVector{Complex{Int64}} with indices 1×2×3×4:
Error showing value of type Base.RootsVector{Complex{Int64}}:
ERROR: MethodError: no method matching unitrange(::Int64)
julia> for i in 1:4
println(roots[i])
end
1.0 + 0.0im
0.0 + 1.0im
-1.0 + 0.0im
-0.0 - 1.0im |
julia> size([1,2,3])
(3,)
julia> size(RootsVector(1+0im, 3))
3 |
How to export it though?
This is fixed now. julia> Base.RootsVector(1+0im, 3)
3-element Base.RootsVector{Complex{Int64}}:
1.0 + 0.0im
-0.5 + 0.8662109375im
-0.5 - 0.8662109375im
julia> Base.RootsVector(1+0im, 4)
4-element Base.RootsVector{Complex{Int64}}:
1.0 + 0.0im
0.0 + 1.0im
-1.0 + 0.0im
-0.0 - 1.0im
I didn't quite understood what you mean by branch point (some examples would be preferable), but I am looking into it how to incorporate it. Shouldn't branch point be julia> sqrt(0+0im)
0.0 + 0.0im
julia> Base.RootsVector(0+0im, 4)
4-element Base.RootsVector{Complex{Int64}}:
0.0 + 0.0im
0.0 + 0.0im
-0.0 + 0.0im
-0.0 - 0.0im
julia> Base.RootsVector(0+0im, 3)
3-element Base.RootsVector{Complex{Int64}}:
0.0 + 0.0im
-0.0 + 0.0im
-0.0 - 0.0im |
You can export it with
julia> x = -1
-1
julia> Δ = 1e-9im
0.0 + 1.0e-9im
julia> sqrt(x + Δ) - sqrt(x - Δ)
0.0 + 2.0im |
|
It seems quite surprising for For implementing this, using |
|
Examples of problems where all roots are actually needed would be interesting to understand the use case for a multivalued |
It was representing julia> roots = RootsVector(1+0im, 4)
4-element RootsVector{Complex{Int64}}:
1.0 + 0.0im
6.123234262925839e-17 + 1.0im
-1.0 + 1.2246468525851679e-16im
-1.8369701465288538e-16 - 1.0im |
Do we have a function which returns roots of unity? I am writting this to generalize for complex numbers beyond just unity. I think |
|
This is how it will work now. I have removed the julia> roots = RootsVector(1+0im, 4)
4-element RootsVector{Complex{Int64}}:
1.0 + 0.0im
6.123233995736766e-17 + 1.0im
-1.0 + 1.2246467991473532e-16im
-1.8369701987210297e-16 - 1.0im
julia> roots = RootsVector(1+0im, 4, 'm')
4-element RootsVector{Complex{Int64}}:
1.0 + 0.0im
6.123233995736766e-17 + 1.0im
-1.0 + 1.2246467991473532e-16im
-1.8369701987210297e-16 - 1.0im
julia> roots = RootsVector(1+0im, 4, 's')
1-element RootsVector{Complex{Int64}}:
1.0 + 0.0im
julia> roots = RootsVector(1, 4)
1-element RootsVector{Int64}:
1.0
julia> roots = RootsVector(1, 4, 'm')
2-element RootsVector{Int64}:
1.0
-1.0
julia> roots = RootsVector(1, 4, 's')
1-element RootsVector{Int64}:
1.0
julia> roots = RootsVector(1, 4, 'm')
2-element RootsVector{Int64}:
1.0
-1.0
julia> roots = RootsVector(1, 4, 's')
1-element RootsVector{Int64}:
1.0Need feedback on julia> roots = RootsVector(-1, 4, 'm')
1-element RootsVector{Int64}:
NaN
julia> roots = RootsVector(-1, 4)
1-element RootsVector{Int64}:
NaN
julia> roots = RootsVector(-1, 4, 's')
1-element RootsVector{Int64}:
NaN
julia> roots = RootsVector(8, 3, 'm')
1-element RootsVector{Int64}:
2.0
julia> roots = RootsVector(8, 3, 's')
1-element RootsVector{Int64}:
2.0
julia> roots = RootsVector(8, 3)
1-element RootsVector{Int64}:
2.0
julia> roots = RootsVector(-8, 3)
1-element RootsVector{Int64}:
-2.0
julia> roots = RootsVector(-8, 3, 'm')
1-element RootsVector{Int64}:
-2.0
julia> roots = RootsVector(-8, 3, 's')
1-element RootsVector{Int64}:
-2.0 |
|
There are a lot of features here. Perhaps it makes sense to prototype in a package first and see if there are many use cases where these features are needed. |
I think for So, I have implemented Also julia> x = -1
-1
julia> Δ = 1e-9im
0.0 + 1.0e-9im
julia> RootsVector(x+Δ, 3, 's')
1-element RootsVector{ComplexF64}:
0.5000000002886753 + 0.8660254036177719im
julia> RootsVector(x-Δ, 3, 's')
1-element RootsVector{ComplexF64}:
0.5000000002886753 - 0.8660254036177719im
julia> RootsVector(x+Δ, 2, 's')
1-element RootsVector{ComplexF64}:
5.000001026025254e-10 + 1.0im
julia> RootsVector(x-Δ, 2, 's')
1-element RootsVector{ComplexF64}:
5.000001026025254e-10 - 1.0im
julia> RootsVector(x+Δ, 2, 's') - RootsVector(x-Δ,2,'s')
1-element Vector{ComplexF64}:
0.0 + 2.0im |
@LilithHafner I think the Suggestions are appreciated. Please confirm if it's good to |
|
There is an infinite set of possible features to add to the language, but it's nice to keep the language itself small. Just because a feature is implemented tested and documented doesn't mean it is appropriate for Base. For example, which use cases motivate the inclusion of both an Feel free to merge master into this branch or rebase this branch on top of the baster branch. I typically prefer it when PR authors merge so that I still have the option to view "changes since last review", but other folks prefer rebasing. Either way the entire PR will get squashed into a single commit to the Julia master branch if it is merged, so there is no need to be particularly fussy about git history, what matters most is the content of the PR, not its git history. As an aside, typically folks use backticks (`) for literal code snippets like |
cispi.(range(0, 2-2/n, n))(if performance matters, it might make sense to do it by repeated multiplication by
What are some examples of this potential usefulness beyond pedagogy? |
|
@LilithHafner |
I am Physics undergrad students, so I thought it might be useful. But I don't have the vantage point to comment on it. Just mention me in the comments if some changes are needed. I would like my first PR to complete all the steps. I would be happy to incorporate the changes the community wants. |
|
There are still several unresolved comments including
These are more design decisions that need to be made than things that need changing in this PR. |
|
I think this is a bad idea. The whole point of an I don't think we want a function to return an array (or iterator) of all roots for complex arguments. I don't think If you want to work on this, I would suggest closing this PR and starting over from scratch. In general, if you want to resolve an issue you should implement the functionality discussed in the issue, not some completely different function. |



So I have written the function nthroot. It returns all the roots in 1D array be it real or complex.
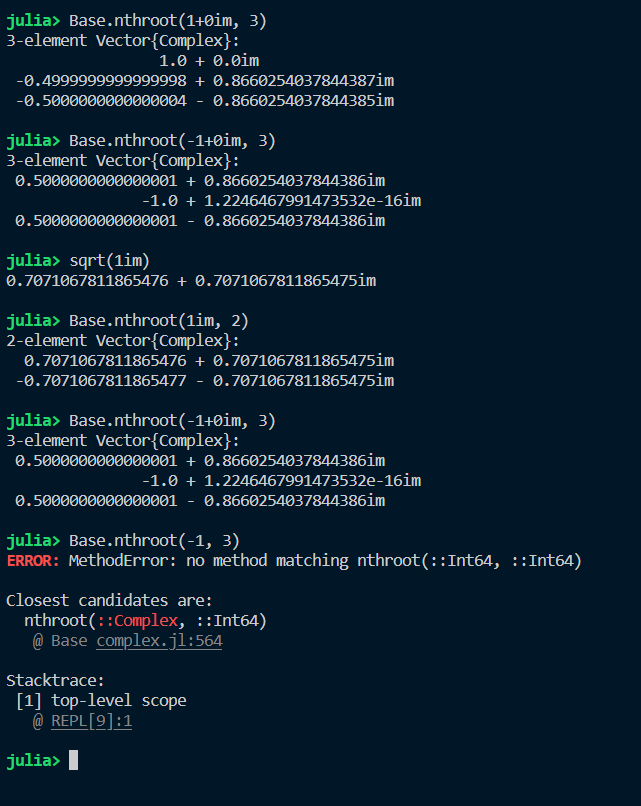
You can see in the above picture that not only it matches sqrt() but also improves it, as the sqrt() reports only one root instead of two. First 4 lines are the examples that the my code is working correctly.
Though I see two points of improvement.
nthroot(-1, 3)andnthroot(-1+0im, 3)to return same thing (will it be a good idea?). Or should I implementnthroot(x::Real, n::Int)so as to return a real value from therootsarray if it exits, else throw an error like belowFeedback would be appreciated!! Also is my function exported correctly?