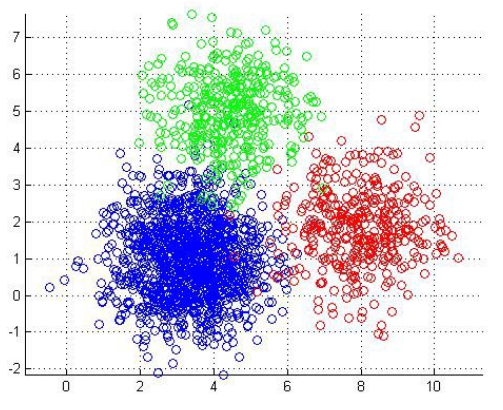
- 层次聚类是一种构建聚类层次结构的聚类算法。该算法从分配给它们自己的集群的所有数据点开始。然后将两个最近的集群合并到同一个集群中。最后,当只剩下一个集群时,该算法终止。
- 可以通过观察树状图来选择最能描述不同组的簇数的决定。聚类数的最佳选择是树状图中垂直线的数量,该水平线可以垂直横穿最大距离而不与聚类相交。
层次聚类(Hierarchical clustering)是一种常见的聚类算法,它将数据点逐步地合并成越来越大的簇,直到达到某个停止条件。层次聚类可以分为两种方法:自下而上的聚合法(agglomerative)和自上而下的分裂法(divisive)。在聚合法中,每个数据点最初被视为一个单独的簇,然后每次迭代将距离最近的两个簇合并为一个新的簇,直到所有点都合并成一个大簇。在分裂法中,最初的簇被视为一个单独的簇,然后每次迭代将当前簇中距离最远的两个点分成两个新的簇,直到每个点都是一个簇为止。
- 使每个数据点成为单点簇→形成N个簇
- 取距离最近的两个数据点,使之成为一个簇→形成N-1个簇
- 取最近的两个簇并使它们成为一个簇→形成N-2个簇。
- 重复第 3 步,直到只剩下一个集群。
有几种方法可以测量聚类之间的距离以确定聚类规则,它们通常称为链接方法。一些常见的链接方法是:
- 完全链接:两个集群之间的距离定义为每个集群中两点之间的最长距离。
- 单链接:两个集群之间的距离定义为每个集群中两点之间的最短距离。此链接可用于检测数据集中的高值,这些值可能是异常值,因为它们将在最后合并。
- 平均链接:两个聚类之间的距离定义为一个聚类中的每个点与另一个聚类中的每个点之间的平均距离。
- Centroid-linkage:找到聚类1的质心和聚类2的质心,然后在合并前计算两者之间的距离。
不同的链接方法导致不同的集群。
树状图是一种显示不同数据集之间的层次关系。正如已经说过的,树状图包含了层次聚类算法的记忆,因此只需查看树状图就可以知道聚类是如何形成的。
import numpy as np
from scipy.cluster.hierarchy import dendrogram, linkage
import matplotlib.pyplot as plt
# 生成随机数据
np.random.seed(0)
X = np.random.randn(15, 2)
# 计算距离矩阵
Z = linkage(X, 'ward')
# 绘制树形图
plt.figure(figsize=(10, 5))
plt.title('Hierarchical Clustering Dendrogram')
plt.xlabel('Sample index')
plt.ylabel('Distance')
dendrogram(
Z,
leaf_rotation=90.,
leaf_font_size=8.,
)
plt.show()在这个示例中,我们首先使用NumPy生成了一个随机的二维数据集X,其中包含15个样本。然后,我们使用SciPy中的linkage函数计算距离矩阵Z,这里使用了“ward”方法来计算簇之间的距离。最后,我们使用Matplotlib来绘制树形图,其中leaf_rotation和leaf_font_size参数用于调整叶子节点的旋转角度和字体大小。
这个示例中生成的树形图显示了不同样本之间的距离,并且根据距离合并了不同的簇。可以通过树形图来确定最优的簇的数量,可以在图中找到最大距离的位置,然后画一条水平线,这个水平线和垂直线的交点就是最优的簇的数量。