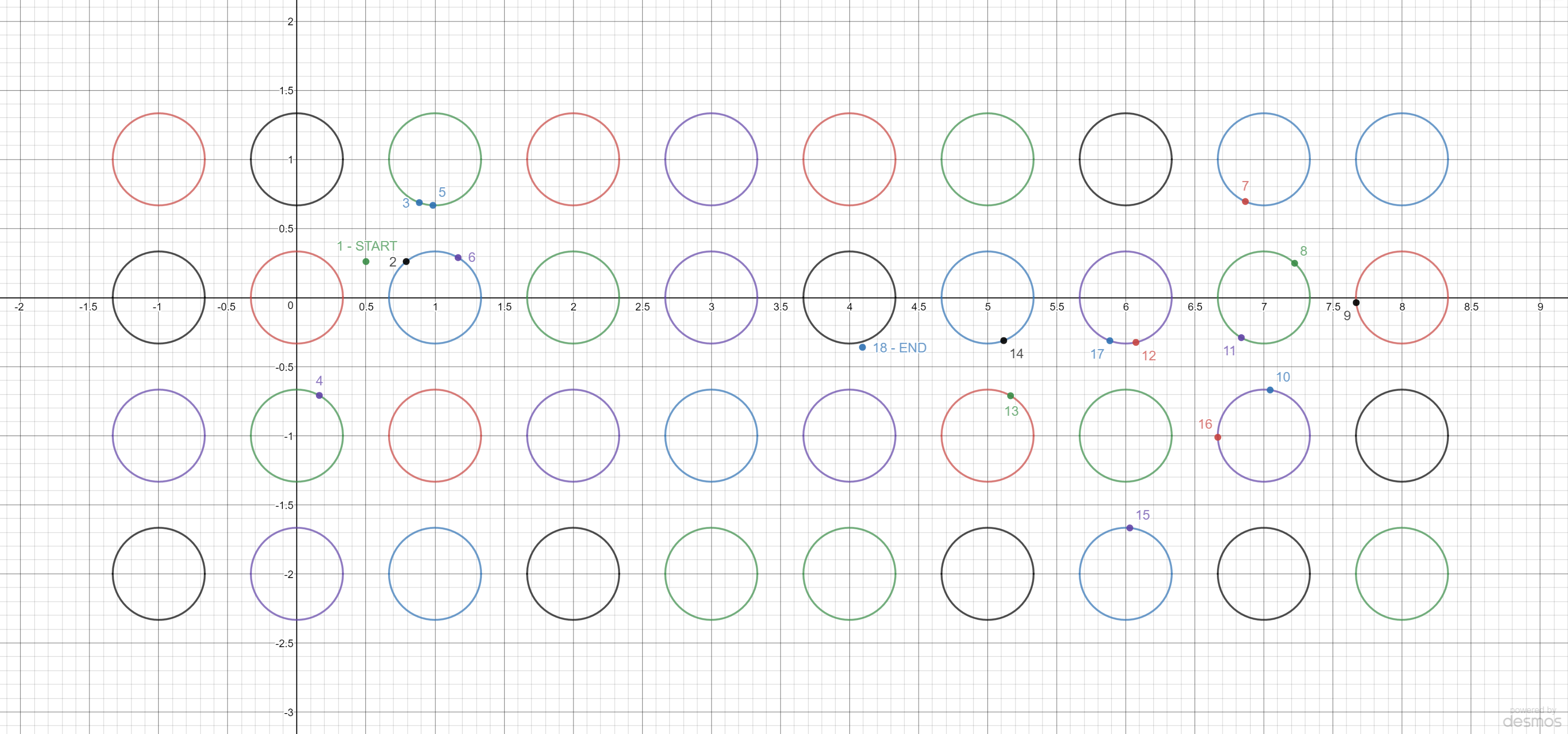
Photon starts moving to the right from point (0.50, 0.26) in a grid lattice with a circular mirror
in each point (R = 1/3) - see Visualization.
The speed of the photon is 1 point per second. Where will the photon be located after t = 20 seconds?
Solving this problem comes down to calculating the reflected line after interaction with the circle. All calculations must be done with very high precision - see Result dependency on precision.
Algorithm used in this project does not use any trigonometric functions nor angles between lines. The only problematic part is calculating the square root, but that can easily be done in arbitrary precision.
These are the points of reflection (impact), except for 1st and 18th point,
rounded to 6 decimal places. All decimal places are correct.
1. (+0.500000, +0.260000) - START
2. (+0.791407, +0.260000)
3. (+0.886170, +0.686705)
4. (+0.162338, -0.708868)
5. (+0.984961, +0.667006)
6. (+1.167217, +0.288356)
7. (+6.866226, +0.694688)
8. (+7.223030, +0.247727)
9. (+7.668756, -0.037259)
10. (+7.045625, -0.669804)
11. (+6.836904, -0.290707)
12. (+6.073914, -0.325035)
13. (+5.166353, -0.711144)
14. (+5.116817, -0.312194)
15. (+6.029651, -1.667988)
16. (+6.666874, -1.011762)
17. (+5.885223, -0.312950)
FINAL POINT:
18. (4.094557, -0.360327) - END
Covered distance:
20.000000
Final points calculated with different values of N are listed below.
N is the number of significant digits used in all calculations.
It is important to notice that a double variable can store up to 15 stable decimal places,
meaning that for values in range <-100, 100> it can store only 17 significant digits.
That is the exact N at which a large computation error occurs.
For this kind of calculations, one must use data types capable of storing numbers in very high precision.
Java's BigDecimal type was used in this project.
N = 50000 => (+4.094557, -0.360327) - correct result
N = 24 => (+4.094557, -0.360327) - correct result
N = 23 => (+4.094557, -0.360328) - change in 6th decimal place
N = 22 => (+4.094556, -0.360306) - change in 5th decimal place
N = 21 => (+4.094557, -0.360325)
N = 20 => (+4.094578, -0.361136) - change in 3rd decimal place
N = 19 => (+4.094611, -0.362331)
N = 18 => (+4.094777, -0.368034)
N = 17 => (+5.645412, +0.906681) - critical error
N = 16 => (+6.468524, -1.785508)
N = 15 => (+6.551874, +1.408657)
N = 14 => (+5.776366, -4.158442)
A small error in locating the impact point will make an error in the equation of the reflected line, which will propagate to the next collision with a lever arm of the free path. Even with exact mathematical equations, numerical errors will occur due to limited calculation precision. These errors will soon accumulate resulting in critical errors such as completely missing a mirror which should have been hit. Using symbolic calculations might seem like a good solution at first, but after just a few reflections the expressions become incredibly complex and calculations are slowed down. Evaluating the final expression on its own might result in large errors due to possible numerical instability.
Image below illustrates the entire problem and solution for t=20s. Each of the reflection points is
labeled with a number, from 1 to 18. Connecting the dots in order will give you the photon's trajectory.
Let us increase the time frame from t=20s to t=200s, keeping all other parameters the same.
At that exact moment the photon will be positioned over point (-15.454298, -7.616898).
This result will be consistently achieved for N=140 and higher. It is quite obvious that using double precision
will produce completely unpredictable outcomes.