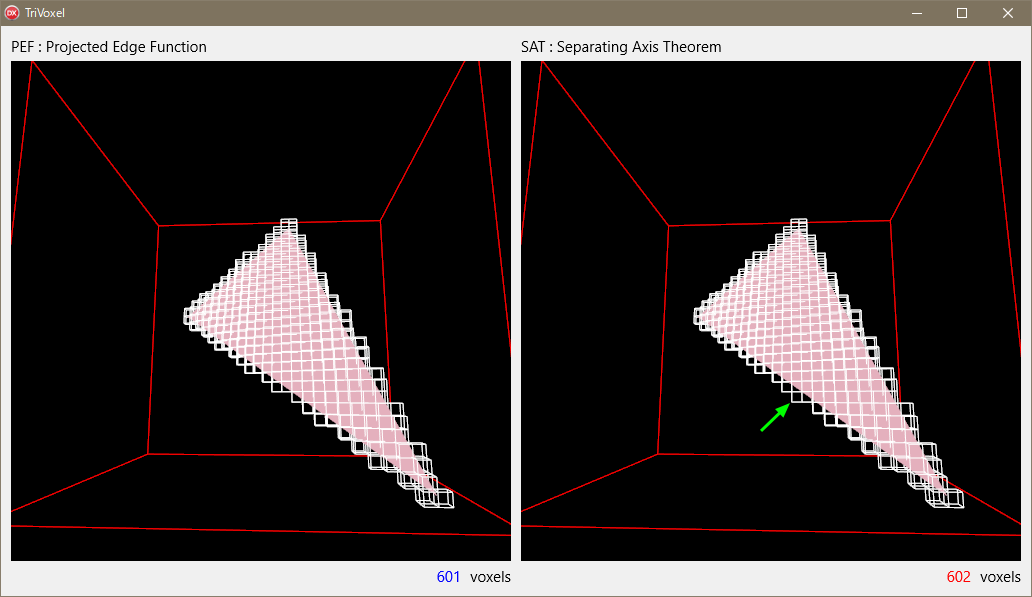
Collision detection between a polygon (triangle) and a voxel (AABB).
ポリゴン:Polygon(三角形)と ボクセル:Voxel(軸平行直方体)との 衝突/交差/干渉を判定(Collision detection) する方法。この手法を利用することで、任意のポリゴンモデルをボクセルモデルへ高速に変換することが可能となる。
アルゴリズムとしては、PEF法 と SAT法 の両方を実装。もちろん"接触"に近い衝突の場合、数値誤差によって結果が曖昧になるが、そのようなレアケースを除いて、本質的に同一の結果が得られることを確認した。
なお、三角形を完全に覆う 26-separating 形式の衝突判定アルゴリズムを対象とする。
3Dでの 点座標 は、以下のレコード型によって定義される。
LUX.D3.pas
3Dでの 軸平行な直方体(AABB:Axis Aligned Bounding Box) は、以下のレコード型によって定義される。
LUX.D3.pas
TSingleArea3D= recordTDoubleArea3D= record
Min:TDouble3D
XYZ軸方向の最小値。Max:TDouble3D
XYZ軸方向の最大値。- function
ProjVec( const Vec_:TDouble3D ) :TDoubleArea
任意のベクトル方向へ射影した1Dの範囲を返す。- function
Collision( const Area_:TDoubleArea3D ) :Boolean
3D-AABB 同士の衝突判定。
3Dでの 三角形平面 は、以下のレコード型によって定義される。
LUX.Geometry.D3.pas
TSingleTria3D= recordTDoubleTria3D= record
Poin1/2/3:TDouble3D
三頂点の座標。- property
Norv:TDouble3D
法線ベクトル。- property
Edge1/2/3:TDouble3D
頂点Poin1/2/3に正対する辺のベクトル。- property
ProjXY:TDoubleTria2D
XY平面上へ投影した2Dの三角形。- property
ProjYZ:TDoubleTria2D
YZ平面上へ投影した2Dの三角形。- property
ProjZX:TDoubleTria2D
ZX平面上へ投影した2Dの三角形。- property
AABB:TDoubleArea3D
三角面を内包する 3D-AABB 。- function
ProjVec( const Vec_:TDouble3D ) :TDoubleArea
任意のベクトル方向へ射影した1Dの範囲を返す。- function
CollisionPEF( const Area_:TDoubleArea3D ) :Boolean
PEF法 による 3D-AABB との衝突判定。- function
CollisionSAT( const Area_:TDoubleArea3D ) :Boolean
SAT法 による 3D-AABB との衝突判定。
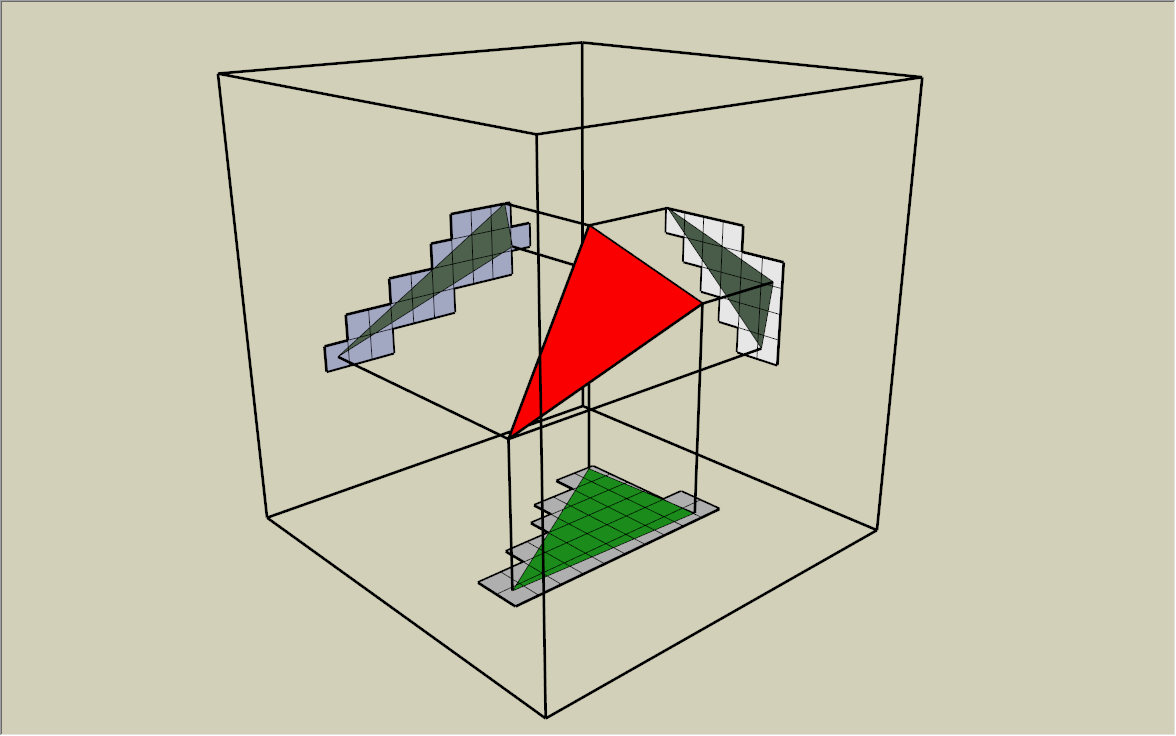
3Dの三角形を XY, YZ, ZX 平面へ投影した上で、2Dの衝突判定を利用する方法。
2Dでの 点座標 は、以下のレコード型によって定義される。
LUX.D2.pas
TSingle2D= recordTDouble2D= record
X/Y:Double
座標値。
2Dでの 軸平行な長方形(AABB:Axis Aligned Bounding Box) は、以下のレコード型によって定義される。
LUX.D2.pas
TSingleArea2D= recordTDoubleArea2D= record
Min:TSingle2D
X/Y軸方向の最小値。Max:TSingle2D
X/Y軸方向の最大値。- function
Collision( const Area_:TSingleArea2D ) :Boolean
2D-AABB 同士の衝突判定。
2Dでの 三角形 は、以下のレコード型によって定義される。
LUX.Geometry.D2.pas
TSingleTria2D= recordTDoubleTria2D= record
Poin1/2/3:TDouble2D
三頂点の座標。- property
Norv:Double
概念的な法線のZ成分。正ならば表。負ならば裏。- property
Edge1/2/3:TDouble2D
頂点Poin1/2/3に正対する辺のベクトル。- property
Enor1/2/3:Double
辺法線:辺に垂直な内側向きのベクトル。- property
AABB:TSingleArea2D
三角形を内包する 2D-AABB 。- function
Collision( const Area_:TDoubleArea2D ) :Boolean
2D-AABB との衝突判定。
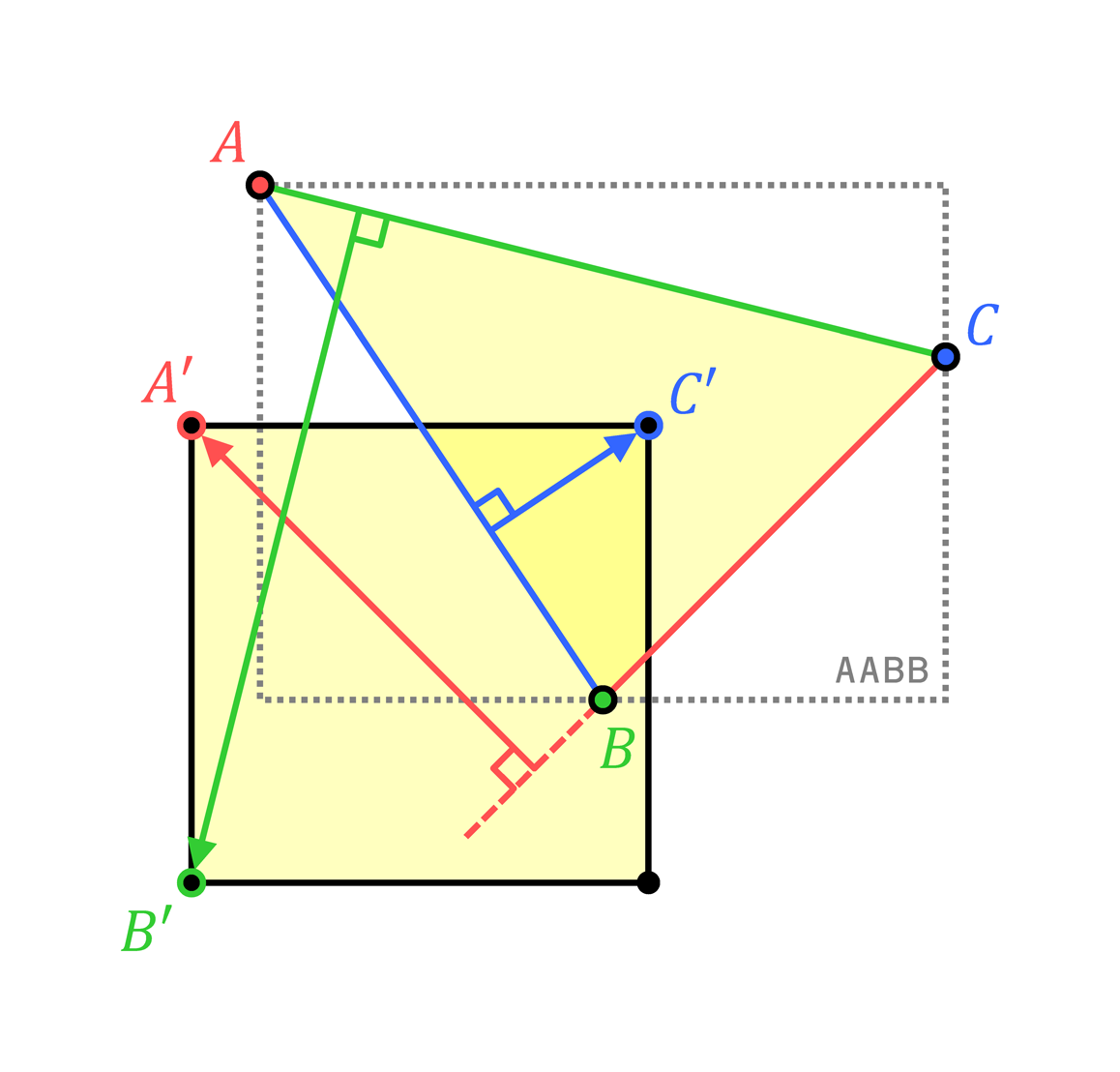
2Dにおける三角形と長方形の衝突判定には、三角形の辺に垂直な内向きのベクトル(辺法線)を用い、以下の2つの条件が満たされる場合、三角形と長方形は衝突していると判定できる。
- 三角形
TDoubleTria2Dの AABB が、長方形TDoubleArea2Dと衝突する。- 三角形の3辺すべてにおいて、辺法線
Enor*の方向に沿って最も前方の長方形の頂点が辺の内側に入る。
function TDoubleTria2D.ColliEdge( const Area_:TDoubleArea2D ) :Booleanメソッドを用いる。
2Dにおける三角形と長方形の衝突判定を実装すると以下のようになる。
function TDoubleTria2D.Collision( const Area_:TDoubleArea2D ) :Boolean;
begin
Result := AABB.Collision( Area_ ) and ColliEdge( Area_ );
end;ただ、第1条件の 2D-AABB 同士の衝突は、わざわざ射影した2D上で判定せずとも、元の3Dでの 3D-AABB 同士の衝突としてまとめることができるので、最終的な実装としては以下のようになる。
function TDoubleTria3D.CollisionPEF( const Area_:TDoubleArea3D ) :Boolean;
//······································
function CheckPlane :Boolean;
begin
~
end;
//······································
begin
Result := AABB.Collision( Area_ )
and CheckPlane
and ProjXY.ColliEdge( Area_.ProjXY )
and ProjYZ.ColliEdge( Area_.ProjYZ )
and ProjZX.ColliEdge( Area_.ProjZX );
end;なお、2Dの衝突判定を3軸方向から行ったとしても、3Dでの衝突判定としては不十分であるため、ポリゴンの法線方向に沿った衝突を判定するCheckPlane関数が加えられている。
分離超平面定理 を利用することで、3次元的にポリゴンとボクセルの衝突判定を行う方法。
[YouTube]
* Separating Axis Theorem (SAT) Explanation.:Hilze Vonck
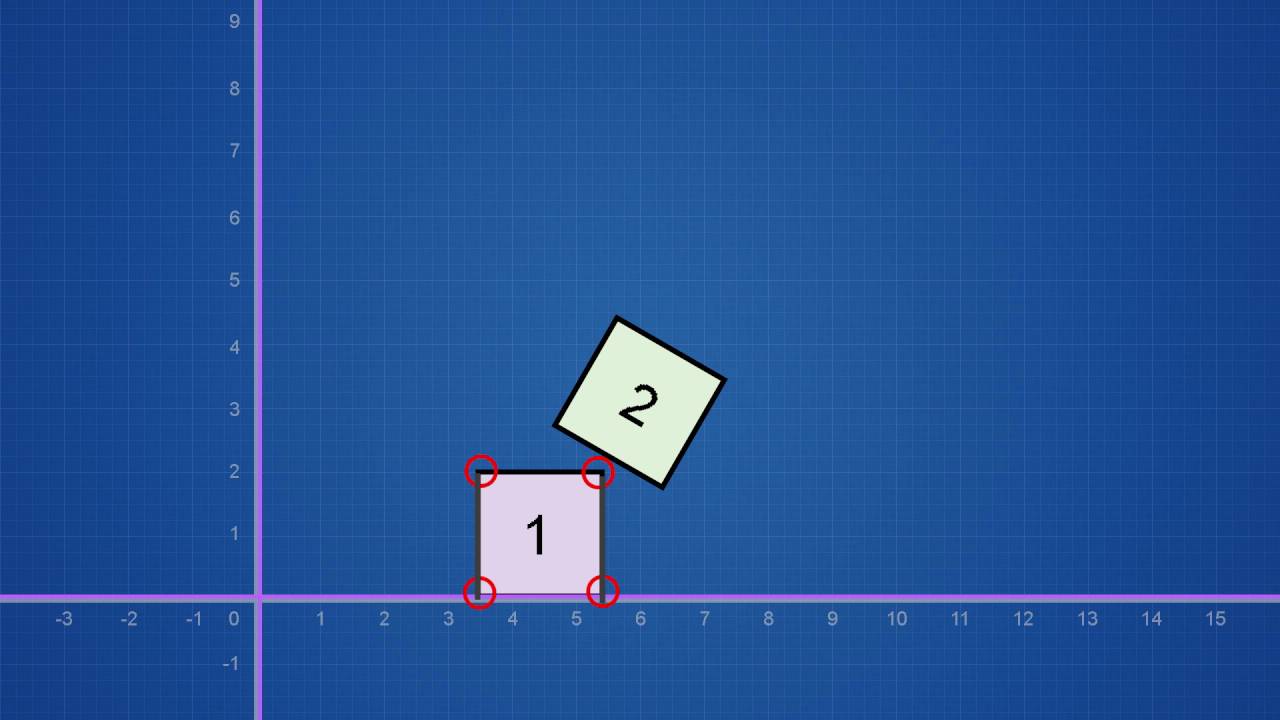
2つの凸体が衝突していなければ、必ず分離面を差し挟むことのできる方向(分離軸:Separating axis)が存在する。つまり、どの方向から見ても隙間が存在しなければ、2つの凸体は衝突している。
具体的には、指定したベクトルVecの垂直方向へ、三角面TriaとボクセルAreaを射影し、その1Dの範囲が重なるかどうかで、分離面の存在が判定できる。
Tria.ProjVec( Vec ).Collision( Area.ProjVec( Vec ) )
さらに、凸体を多面体に限るのであれば、調べるべき方向の数は有限となる。 特にポリゴンとボクセルの場合、以下の 13方向 について調べるだけでよい。
- 三角面の法線
- ボクセルの法線
- X軸方向
- Y軸方向
- Z軸方向
- ボクセルの法線 × 三角面の辺 ※ ×:外積
- X軸 × A辺
- X軸 × B辺
- X軸 × C辺
- Y軸 × A辺
- Y軸 × B辺
- Y軸 × C辺
- Z軸 × A辺
- Z軸 × B辺
- Z軸 × C辺
* Improvements of the Voxmap-PointShell Algorithm - Fast Generation of Haptic Data-Structures:ResearchGate
具体的な実装は以下のようになる。
function TDoubleTria3D.CollisionSAT( const Area_:TDoubleArea3D ) :Boolean;
//······································
function CheckPlane :Boolean;
begin
~
end;
//·································
function Check( const Vec_:TDouble3D ) :Boolean;
begin
Result := ProjVec( Vec_ ).Collision( Area_.ProjVec( Vec_ ) );
end;
//······································
const
AX :TDouble3D = ( X:1; Y:0; Z:0 );
AY :TDouble3D = ( X:0; Y:1; Z:0 );
AZ :TDouble3D = ( X:0; Y:0; Z:1 );
var
E1, E2, E3 :TDouble3D;
begin
E1 := Edge1;
E2 := Edge2;
E3 := Edge3;
Result := AABB.Collision( Area_ ) // Check( AX ) and Check( AY ) and Check( AZ )
and CheckPlane // Check( Norv )
and Check( CrossProduct( AX, E1 ) )
and Check( CrossProduct( AX, E2 ) )
and Check( CrossProduct( AX, E3 ) )
and Check( CrossProduct( AY, E1 ) )
and Check( CrossProduct( AY, E2 ) )
and Check( CrossProduct( AY, E3 ) )
and Check( CrossProduct( AZ, E1 ) )
and Check( CrossProduct( AZ, E2 ) )
and Check( CrossProduct( AZ, E3 ) );
end;ここでX/Y/Z軸方向の分離判定は 3D-AABB との衝突判定と等価であり、さらに三角面の法線方向の分離判定は前述のCheckPlane関数と等価である。
- The Basics of GPU Voxelization:NVIDIA Developer
- GPU上でのvoxel構築手法:shikihuiku
- Improvements of the Voxmap-PointShell Algorithm - Fast Generation of Haptic Data-Structures:ResearchGate
- Fast Parallel Surface and Solid Voxelization on GPUs:Michael Schwarz
- VoxelPipe: A Programmable Pipeline for 3D Voxelization:NVIDIA Research