python modules to evaluate methylation modeling strategies and find differentially methylated regions.
See additional documentation here
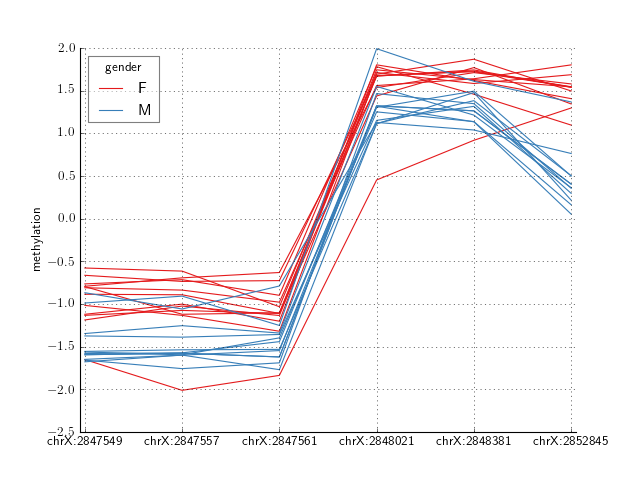
Here is an example of a region discovered by crystal where males have lower methylation than females
All functions to model clusters take:
- formula: a string model formula in R (or patsy syntax).
- a methylation cluster from aclust
- a pandas datafame containing the covariates of interest. The samples in this dataframe should be in the same order as they are in the methylation cluster.
- a coefficient of interest from the model.
So a single call would look like:
import pandas as pd
import aclust
import crystal
covs_df = pd.read_csv('covariates.csv')
cluster_iter = aclust.mclust(feature_gen(), max_dist=100)
crystal.zscore_cluster("methylation ~ disease + age + gender",
next(cluster_iter),
covs_df,
"disease")Which will return a dictionary containing the p value, the coef
and the t statistic for 'disease' status. However it is more likely
that users will want a simple way to model every cluster:
for cluster in crystal.model_clusters(cluster_iter, covs_df,
formula, "disease",
crystal.zscore_cluster, n_cpu=10):
print clusterSee the introduction notebook for more detail
users unaccustomed to installing their own python packages should
download anaconda and
then install additional modules with pip.
Running python setup.py install should work on systems with the
scientific python stack.
Crystal works by generating clusters using aclust and then testing them against a chosen method. New methods can be implemented easily, but currently, there is:
- GEE: generalized estimating equation using sample as the grouping variable
- Mixed Effect Model: with a random intercept by sample
- Combining P-values: test each site in a region and combine the resulting p-values using the Stouffer-Liptak or Z-score method
- Bump(hunt)ing: A modification of bumphunting that works on local clusters and allows arbitrary metrics (not just the sum of the smoothed coefficients).
Methods using Robust regression are also available for the above.
Note that these are cleanly implemented in python thanks to the excellent statsmodels package
I have evaluated a number of methods for modeling correlated data (clusters). See the evaluation notebook for more detail. Here is the summary image--higher is better for the top plot and lower is better for the bottom plot: