To install the graphical interface GoGui[14] and the player GnuGo[13], execute:
./install_env.sh
To compile our programs:
make all
Inside the folder bin you will find: marcos_(tateti|connect4|hexa|go) and marcos_debug, which is a special compilation of the Go player with enabled debug flags.
The program can be used by console through commands provided by Go Text Protocol[15].
On the other hand, if you want a friendlier user interface, you can use GoGui. A sample script is provided: "play_game" (You can also start GoGui and configure it).
To play a game between our program and GnuGo through visual interface, you can use the "play_game_vs_gnu" script.
- boardsize int , Determines the size of the board.
- clear_board , Clean the board, ie, restart the game.
- genmove (w|white|b|black) , Generates a movement for the right player.
- play (w|white|b|black) mov , Performs a certain movement for the right player. The movement may be a coordinate on the board, "pass" (pass) or "resign" (give up).
- showboard , Display the board.
- komi value , Determines the komi value (compensation for the white player).
- final_score , Displays the final score of the game.
- quit , Finish the game.
If you run the debug version, you will have two more commands:
- match_patterns , Shows board positions that match patterns, capture movements and atari escape.
- debug Displays information about the internal representation of board as: grouping of blocks, the number of free adjacencies of each block, status within the MCTS tree for each board position (number of visits and current estimation), etc.
Within the implementation of the program there are several variables that can be modified and influence how the program progresses. Several command line options were implemented to allow you to configure each of them without recompiling the code (if not be present, a default value is taken).
- --help , Displays available options.
- --patterns file_name (No file) Determines the input file from which read the 3x3 patterns.
- --bandit_coeff double (0) Specify exploration coefficient.
- --amaf_coeff double (2500) Specify the K value for the RAVE extension.
- --fill_board double (1) Number of attempts per cycle to fill the board.
- --long_game_coeff double (3) Specify the coefficient to be multiplied by the size of the board to determine the maximum number of moves per simulation.
- --limit_expansion int (1) Determine the number of simulations required before expanding a node.
- --cycles_mcts int (30000) Determines the number of cycles of the algorithm MCTS before a mov.
- --threads_mcts int (5) Determines the number of threads to run parallel.
- --resign_limit double (0.1) Determines the minimum probability of winning the game to continue playing.
- --root_parallel (False) Enables parallelization using the ``Root Parallel" approach.
- --japanese_rules (China) Activates the Japanese score (by territory).
- --totally_random_sim (False) Disables the use of patterns and captures. Totally random simulations.
- --no_rave (Rave) Disables the use of Rave extension.
Para instalar la interfaz gráfica GoGui[14] y el jugador GnuGo[13], ejecutamos:
./install_env.sh
Para compilar nuestros programas:
make all
Dentro de la carpeta bin obtendremos los binarios marcos_(tateti|connect4|hexa|go) y marcos_debug que es una compilación del jugador de Go con banderas de debug activadas que nos permiten obtener información extra en la ejecución del programa.
El programa se puede utilizar por consola a través de los comandos provistos por Go Text Protocol[15].
Por otro lado, si se desea una interfaz más amigable, se puede recurrir a la interfaz visual GoGui. Para esto, se provee un script de ejemplo: "play_game" (También se puede iniciar GoGui y configurarlo utilizando las opciones provistas en la barra de tareas).
Para jugar una partida entre nuestro programa y GnuGo a través de la interfaz visual, se puede utilizar el script "play_game_vs_gnu".
- boardsize int , Determina el tamaño del tablero.
- clear_board , Limpia el tablero, es decir, reinicia el juego.
- genmove (w|white|b|black) , Genera un movimiento para el jugador indicado.
- play (w|white|b|black) mov , Realiza un movimiento determinado para el jugador indicado. El movimiento puede ser una coordenada en el tablero, "pass" (pasar) o "resign" (rendirse).
- showboard , Mostrar el tablero.
- komi value , Determina un valor de komi (compensación al jugador blanco).
- final_score , Muestra el puntaje final del juego.
- quit , Termina el juego.
Si ejecutamos la versión de debug, contaremos con 2 comandos más:
- match_patterns , Muestra las posiciones del tablero que concuerdan con patrones, movimientos de captura y escape de atari.
- debug Muestra varios datos respecto a la representación interna del tablero como ser la agrupación por bloques, el número de adyacencias libres en cada bloque y el estado dentro del árbol de MCTS para cada posición del tablero (número de visitas y estimación actual).
Dentro de la implementación del programa hay varias variables que se pueden modificar e influyen en la forma que el programa progresa. Se implementaron varias opciones de linea de comando que permiten configurar cada una de ellas sin necesidad de recompilar el código (en caso de no estar presentes, se toma un valor por defecto).
- --help , Muestra las opciones disponibles.
- --patterns file_name (No file) Determina un archivo sobre el cual leer los patrones de 3x3.
- --bandit_coeff double (0) Determina un valor determinado al coeficiente de exploración.
- --amaf_coeff double (2500) Determina el valor K de la mejora Rave.
- --fill_board double (1) Determina el número de intentos ``fill_board" por ciclo en simulación.
- --long_game_coeff double (3) Determina el coeficiente que se multiplicará por el tamaño del tablero para determinar el número máximo de movimientos por simulación.
- --limit_expansion int (1)Determina el número de simulaciones necesarias antes de expandir un nodo.
- --cycles_mcts int (30000) Determina el número de ciclos del algoritmo MCTS antes de realizar un mov.
- --threads_mcts int (5) Determina el número de threads a correr en paralelo.
- --resign_limit double (0.1) Determina el mínimo de esperanza de ganar el juego necesario para continuar una partida.
- --root_parallel (False) Activa la paralelización utilizando el enfoque ``Root Parallel".
- --japanese_rules (China) Activa la puntuación Japonesa (por territorio).
- --totally_random_sim (False) Desactiva el uso de patrones y capturas, por simulaciones totalmente aleatorias.
- --no_rave (Rave) Desactiva el uso de la mejora Rave.
Como trabajo final de la materia Introducción a la Inteligencia Artificial, se decidió implementar un programa que juegue al juego Go. Informándose acerca del estado del arte, se puso en manifiesto que el enfoque principal que se utiliza hoy en día para enfrentar este problema son los programas construidos sobre el algoritmo de Monte Carlo Tree Search.
El Go ha sido considerado siempre un gran desafío para la Inteligencia Artificial. Uno de los mayores obstáculos para la construcción de un programa, ha sido la dificultad de conseguir una adecuada función de evaluación. Para hacer frente a esta dificultad, surgió el algoritmo de MCTS, que permite evaluar una posición simulando un conjunto de partidas partiendo de dicha posición y analizando los resultados obtenidos al final.
Monte Carlo Tree Search (MCTS) es un método para toma óptima de decisiones en problemas de Inteligencia Artificial. Combina la generalidad de simulaciones aleatorias con la precisión de una búsqueda en el árbol de posibilidades.
MCTS no requiere una función de evaluación de posición, en contraste con la búsqueda alfa beta. Está basado en una exploración aleatoria del espacio de búsqueda, pero usa los resultados de previas exploraciones. Para ello, MCTS construye gradualmente un árbol en memoria, que mejora sucesivamente estimando los valores de los movimientos más prometedores.
Para que MCTS sea aplicable se debe cumplir: la puntuación del juego debe estar acotada, las reglas son conocidas (información completa) y las simulaciones terminan relativamente rápido (longitud del juego es limitada) [1].
MCTS ofrece ciertas ventajas sobre los métodos tradicionales de búsqueda en árboles [16]:
-
Sin Heurísticas: MCTS no requiere ningún conocimiento estratégico del dominio de aplicación para lograr decisiones razonables. El algoritmo puede funcionar efectivamente sin conocimiento del juego fuera de los estados posibles y la condición final. Esto permite que sus implementaciones sean fácilmente reusables.
-
Asimétrico: MCTS incrementa el tamaño del árbol de búsqueda de manera asimétrica, adaptándose a la topología del espacio de búsqueda. Es decir, enfoca su búsqueda en las partes más relevantes del árbol. Esto otorga grandes beneficios en juegos con un gran factor de crecimiento del espacio de estados.
-
Cuanto tiempo se desee: El algoritmo puede ser interrumpido en cualquier momento y obtener la mejor estimación hasta este punto.
-
Simple de implementar.
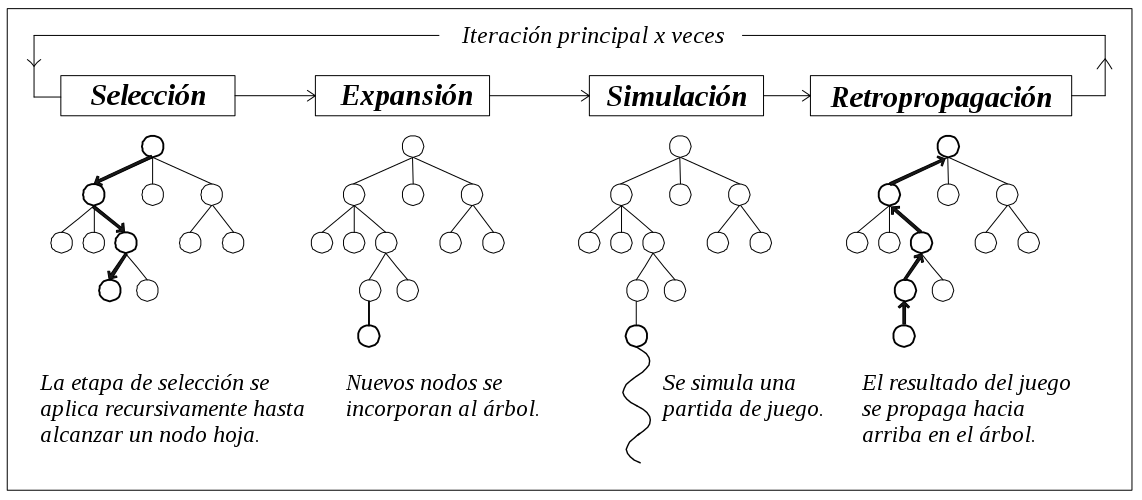
Etapas del algoritmo MCTS [6].
MCTS consiste en cuatro etapas principales, repetidas tantas veces como tiempo se disponga. En cada una de las iteraciones se parte de la situación actual del juego.
-
Selección: El árbol se recorre desde el nodo raíz hasta alcanzar un nodo hoja. Se toma una rama u otra dependiendo de la estrategia de selección que se emplee y la información almacenada en el nodo en ese momento, como el valor y el número de visitas.
Dentro de las diferentes opciones, UCT (Upper Confidence bounds applied to Trees) [4] es la más utilizada por su simplicidad y eficiencia. La estrategia UCT calcula para cada uno de los movimientos posibles una combinación de dos valores, la tasa de éxito de ese nodo y un número asociado a la relación entre el número de veces que se ha visitado el nodo padre y el número de veces que se visitó dicho nodo(hijo). El primer valor está relacionado con la explotación y el segundo con la exploración. A través de un coeficiente C utilizado en la combinación de ambos valores, se puede dar mayor prioridad a la explotación o exploración.
Otro punto a favor de la estrategia UCT, es su independencia del dominio de aplicación.
Fórmula UCT:
$ValUCT(N_i) = tasaExito_i + C * \sqrt{ln(n_p) / n_i}$ Donde:
$n_p$ y$n_i$ son el número de visitas al nodo padre y al nodo$N_i$ respectivamente, C es el coeficiente de exploración. -
Expansión: Se añaden nodos al árbol MCTS según una estrategia de expansión.
Según el criterio, se puede expandir siempre que se visite un nodo, o cuando se alcanza un determinado número de visitas mínimo, lo que permite ahorrar espacio en memoria, regulando cuánto crece el árbol en relación al número de ciclos del algoritmo.
Además, se pueden tomar dos caminos a la hora de expandir: en cada expansión añadir un solo nodo hijo de todos los posibles movimientos o añadir directamente todos los nodos hijos.
-
Simulación: Se realiza una partida simulada partiendo del nodo hoja alcanzado en las fases anteriores. Durante esta partida, el programa juega solo, realizando los movimientos de todos los jugadores que intervienen hasta que la partida finalice y se obtenga un resultado.
Las estrategias que se utilizan consisten o bien utilizar movimientos aleatorios o combinar la aleatoriedad con una heurística asociada al problema concreto. En estos casos es necesario buscar un equilibrio entre la exploración, que da la aleatoriedad, y la explotación, que dirige hacia un movimiento más prometedor.
-
Retropropagación: El resultado de la simulación se propaga hacia los nodos atravesados previamente. Partiendo del nodo hoja y subiendo por la relación con los nodos padres hasta llegar a la raíz, se actualiza cada nodo, incrementando en una unidad el número de visitas y actualizando su valor con el resultado de la simulación.
Por último, a la hora de seleccionar el movimiento final, se considerará el mejor hijo del nodo raíz, es decir, el movimiento más prometedor de acuerdo a la información recaudada. Para determinar qué nodo "es mejor" se pueden tomar diferentes criterios, considerando la tasa de éxito, o el número de visitas, etc. De acuerdo a experimentos realizados, no hay una diferencia significativa entre las diferentes opciones, si se realiza un número suficiente de simulaciones.
Para la implementación del algoritmo MCTS, principalmente se buscó:
-
Que sea reutilizable, es decir, que la implementación del árbol y el algoritmo MCTS sean independiente del dominio de aplicación, y además se puedan agregar nuevos módulos para modificar diferentes etapas del algoritmo (Selección, Expansión, Simulación, etc.), en caso de tomar diferentes criterios.
-
Que sea eficiente. Este punto siempre estuvo presente en la implementación. Para lograr buenos resultados, resulta vital realizar la mayor cantidad de ciclos del algoritmo en el menor tiempo posible. Por esto, se intentó optimizar en todo lo posible, y en muchas casos se recurrió al uso de templates, funciones "inline", guardar cachés de ciertos valores para evitar hacer cálculos redundantes, sobretodo de funciones costosas (por ejemplo las llamadas a log() y sqrt() en las selecciones uct y rave), etc.
Buscando un código reusable, se decidió abstraer toda la lógica del dominio de aplicación en una clase State y un tipo Data. La clase State abstrae las formas en que puede transicionar el sistema, todas las reglas de juego, el cálculo de puntajes, los posibles pasos a tomar en un determinado punto, etc. El tipo Data, almacenará los datos de una transición a realizar en un determinado momento, por ejemplo, en el caso del tateti, Data almacenará las coordenadas de la ficha a incorporar y si es cruz o círculo.
State, luego, contará con una interfaz mínima:
class State{
// Crear una copia del estado.
State(State *src)
// Obtener una lista de posible pasos a realizar desde dicho estado.
// Si es vacía, se llegó al final.
get_possible_moves(vector<Data>& v)
// Aplicar un paso en particular. (transición)
apply(Data)
// Obtener el resultado final.
Value get_final_value()
}
De la cual heredarán por ejemplo: StateTateti, StateGo, StateConnect4, etc. Cada nodo del árbol almacenará información Data, de un movimiento determinado.
Entonces, partiendo de un estado inicial, podemos ir recorriendo el árbol desde la raíz, aplicando los pasos que se encuentran en cada nodo hasta llegar a una hoja, donde se iniciará la simulación. De esta manera se evita almacenar un estado en cada nodo, almacenando únicamente los datos de la transición realizada (Data).
Para las 4 etapas principales: Selección, Expansion, Simulación, Retropropagación, se crearon clases abstractas con las interfaces mínimas necesarias para llevar a cabo el algoritmo.
Diferentes implementaciones que corresponden a diferentes criterios, pueden heredar de cada una de ellas, como por ejemplo: SelectionUCT, implementará la selección utilizando el algoritmo UCT, mientras que SelectionUCTRave, incorporará además la evaluación amaf siguiendo la propuesta de optimización RAVE.
Con respecto a la paralelización del algoritmo, se consideraron diferentes opciones, de igual manera a las mencionadas en [3]. Luego de hacer algunas pruebas con diferentes enfoques, se decidió proseguir con el principio de Tree Parallelization ([3]) con un lock global. En este enfoque, cada thread bloqueará el árbol cuando necesite acceder al mismo, en las etapas de selección, expansión y retropropagación. Puede parecer muy limitante, pero como el mayor tiempo se pierde en la etapa de simulación, este criterio termina siendo muy válido y se pueden lograr resultados muy buenos con una implementación muy simple, solamente de debe agregar un lock global para el acceso al árbol.
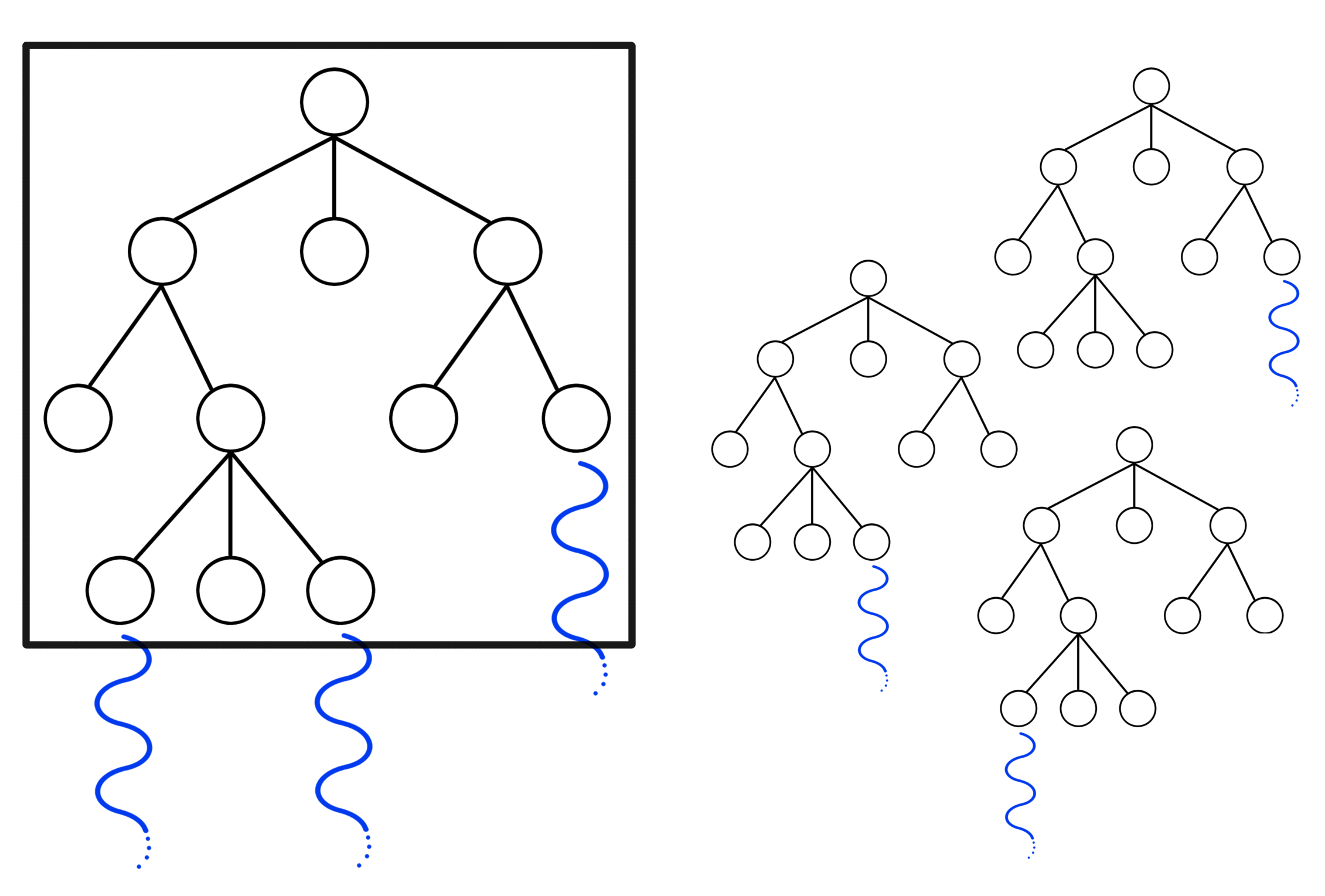
También, como segunda opción, se implementó el enfoque Root Parallelization, debido a que se mencionaban muy buenos resultados en la documentación [3]. Root Parallelization consiste en mantener un árbol distinto para cada thread que actúa de forma independiente al resto y, al finalizar, se unen en un solo árbol sobre el que analiza el mejor movimiento. Esto permite el máximo de concurrencia, ya que cada thread actúa de forma independiente, pero al costo de tener mucho mas información almacenada en memoria. En nuestro caso, no se lograron mejoras en el tiempo de ejecución ni en la porcentaje de partidas ganadas, por el contrario, resultó en una leve desmejora, por lo que se prosiguió con el enfoque de Tree Parallelization. Sin embargo, Root Parallelization es soportado y se puede activar a través de una bandera.
Diferentes enfoques de paralelización MCTS. [3]
Para testear la implementación del algoritmo MCTS con algunos ejemplos simples, se implementaron diferentes juegos. Básicamente, fue necesario implementar la lógica del juego en una clase que herede de State y añadir la posibilidad de que el usuario pueda interactuar jugando a través de la consola.
Las estrategias utilizadas en cada etapa fueron:
-
Selección: UCT.
-
Expansión: Luego de 2 visitas, se expanden todos los hijos posibles.
-
Simulación: Movimientos totalmente aleatorios.
-
Retropropagación: Simple, actualizando las tasa de éxito y num. de visitas.
-
Selección del resultado: Más Robusta, que consiste en elegir el nodo hijo con mayor número de visitas.
Tendremos un tablero de 3x3 y cada paso consistirá en el ingreso de una ficha en una posición vacía. El objetivo será lograr una linea de 3 fichas iguales (Diagonal/Vertical/Horizontal).
Tendremos un tablero de 6x7 y cada paso consistirá en el ingreso de una ficha en una columna con al menos una posición vacía. El objetivo será lograr una linea de 4 fichas iguales (Diagonal/Vertical/Horizontal).
Tendremos un tablero de 11x11 y cada paso consistirá en el ingreso de una ficha en una posición vacía. El objetivo será lograr una cadena de fichas iguales que conecten ambos extremos del tablero. A diferencia de los dos ejemplos anteriores, en este caso el factor de crecimiento del árbol (11*11=121) es mucho mayor. Para poder hacer frente a esto, se recurrió a la mejora llamada RAVE. Siguiendo este criterio se lograron mucho mejores resultados.
El Go es un juego de tablero estratégico para dos jugadores. Durante el juego, los jugadores se alternan para colocar piedras sobre las intersecciones vacías de una cuadrícula, sujetos a algunas restricciones; o pasando (no colocando ninguna piedra en su turno). A un jugador se le llama blanco y a otro negro, según el color de sus piedras. Negro mueve primero. Una vez colocada una piedra, no se mueve por el resto del juego. Una piedra o cadena de piedras del mismo color es capturada y retirada del juego si después de una jugada, no posee intersecciones vacías adyacentes, esto es, si se encuentra completamente rodeada por piedras del color contrario en todas sus intersecciones directamente adyacentes. El objetivo del juego es obtener la mayor puntuación al final del juego.
Existen diferentes formulaciones de las reglas del juego, pero todas concuerdan en los aspectos generales y las diferencias no afectan significativamente la estrategia ni el desarrollo del juego salvo en situaciones excepcionales. El juego termina después de 2 pases consecutivos; esto ocurre cuando ningún jugador piensa que existan más movimientos convenientes y por lo tanto decide no mover (Pasa).
En todas las reglas se tiene en cuenta el territorio (cada una de las regiones del tablero rodeadas por piedras de un único color) como parte de la puntuación. En la puntuación Japonesa, la puntuación consiste en la cantidad de territorio propio más la cantidad de piedras enemigas capturadas, y también el komi para blanco, que es un valor plus que se le otorga al jugador blanco para compensar la desventaja de empezar en segundo lugar. En cambio, en la puntuación China, en vez de contar las piedras capturadas, se suman las piedras de color propio presentes en el tablero.
A pesar de que las reglas de Go son simples, la estrategia es extremadamente compleja e involucra balancear muchos requisitos, algunos contradictorios. Por ejemplo, ubicar piedras juntas ayuda a mantenerlas conectadas y si una está viva, también lo estarán las demás. Por otro lado, colocarlas separadas permite tener influencia sobre una mayor porción del tablero con la posibilidad de apropiarse de más territorio. Parte de la dificultad estratégica del juego surge a la hora de encontrar un equilibrio entre estas dos alternativas. Los jugadores luchan tanto de manera ofensiva como defensiva y deben elegir entre tácticas de urgencia y planes a largo plazo más estratégicos.
Go Text Protocol (GTP)[15] es un protocolo basado en texto para la comunicación con programas que juegan al Go. A través del intercambio de comandos, se puede establecer partidas entre diferentes programas, programas y usuarios y conectarse con servidores para participar de torneos.
El proyecto desarrollado, soporta este protocolo. Esto nos permitió testear los diferentes avances jugando contra otros programas, como GnuGo[13], y contra diferentes variantes de si mismo.
Al mismo tiempo, también nos posibilitó comunicarnos con una interfaz visual, como ser GoGui[14], pudiendo así jugar de manera más amigable y testear el programa durante su desarrollo.
Para almacenar el estado del juego, se recurre por un lado a una matriz que almacene las posiciones del tablero (Blanco/Negro/Vacío).
Por otro lado, debemos representar de alguna manera la noción de "Bloque". Para esto, se buscó la implementación que nos permita realizar las operaciones sobre ellos lo más eficientemente posible. Las principales operaciones y su complejidad de acuerdo a la implementación elegida son:
-
Saber si el bloque está rodeado por fichas del color opuesto. O(1)
-
Saber a qué bloque pertenece una ficha en una posición. O(1)
-
Agregar fichas a un bloque. O(1)
-
Unir 2 bloques. O(n)
-
Eliminar del tablero las fichas de un bloque. O(n)
El algoritmo MCTS calcula por separado el valor de cada estado y cada acción en el árbol de búsqueda. Como resultado, no se puede generalizar entre las posiciones o movimientos relacionados. Para determinar el mejor movimiento, muchas simulaciones deben realizarse a partir de todos los estados y de todas las acciones.
El algoritmo RAVE[2], utiliza la heurística "all-moves-as-first" , desde cada nodo del árbol de búsqueda, para estimar el valor de cada acción. Proporciona una forma sencilla de compartir conocimientos entre los nodos relacionados en el árbol de búsqueda, lo que resulta en una estimación rápida del valor de cada acción. Esta estimación a menudo puede determinar la mejor jugada después de sólo un puñado de simulaciones, y se puede utilizar para mejorar significativamente el rendimiento del algoritmo de búsqueda.
Esta mejora está basada en el hecho de que en ciertos juegos incrementales, como el Go, el valor de una acción a menudo no está afectada por movimientos jugados en otro lugar en el tablero. Entonces, la idea subyacente de all-moves-as-first es tener un valor general para cada movimiento, independientemente del momento en que se juega.
De esta manera, la heurística AMAF proporciona órdenes de magnitud más información: cada movimiento típicamente se ha intentado en varias ocasiones, después de sólo un puñado de simulaciones.
RAVE propone generalizar sobre los sub-árboles con la asumpción de que el valor de una acción a en un estado s será similar en cualquier punto del sub-árbol de s. Luego, el valor de a es estimado a partir de todas las simulaciones que parten de s e incluyen en algún momento el paso a, sin importar exactamente cuándo se realiza.
El algoritmo RAVE aprende muy rápidamente, pero a menudo es equivocado. La principal asumpción de RAVE, que un movimiento en particular tiene el mismo valor en todo un sub-árbol, se viola con frecuencia.
Este problema se supera mediante la combinación del aprendizaje rápido del algoritmo RAVE con la precisión y la convergencia del algoritmo MCTS. Para estimar el valor total de la acción a en un estado s, usamos una suma ponderada, entre el valor amaf y el valor mc en dicho nodo:
MCamaf
Donde p se irá modificando a medida que se realizan mayor número de
simulaciones. Valiendo p(N_i) \approx 1 cuando n_i (num de
simulaciones) es un número menor y un valor
Si además incorporamos el componente de exploración de la selección UCT, obtenemos una nueva fórmula para el algoritmo de selección:
UCT-RAVE[2]: ValUCTRave(N_i) = (1-p(N_i)) * tasaExito_i + p(N_i) * amaf_i + C * \sqrt{ln(n_p) / n_i}
Donde: n_p y n_i son el número de visitas al nodo padre y al nodo N_i respectivamente, C es el coeficiente de exploración y p es el coeficiente que determina la relación entre la estimación amaf y la tasa de éxito.
Se decidió definir el valor de p de acuerdo al enfoque "Hand-Selected Schedule" [2]. El cual utiliza un parámetro k que determina el número de simulaciones en el cual p asignará igual peso a la tasa de éxito y a la estimación amaf.
p(N_i)= \sqrt{k / (3n_i+k)}*
Esta mejora se implementó a nuestro algoritmo de MCTS de la siguiente manera:
-
Incorporando una nueva clase SelectionUCTRave que hereda de la clase abstracta Selection y implementa la funcionalidad antes descripta.
-
Fue necesario modificar los nodos del árbol para llevar cuenta de los valores amaf.(NodeUCTRave)
-
Crear una clase MoveRecorder que lleva el registro de los movimientos realizados en una simulación. (y por lo tanto modificar el proceso de simulación para que utilice esta clase).
-
Modificar el algoritmo de retropropagación para que actualice adecuadamente los valores amaf de los sub árboles de acuerdo a los movimientos registrados en la simulación.
Nuevamente, se buscó una implementación independiente del dominio de aplicación.
Con el objetivo de mejorar el algoritmo, y habiendo agotado las principales opciones independientes del dominio de aplicación, se decidió considerar algunas alternativas a partir de la incorporación de conocimiento propio del juego Go.
Las principales etapas sobre las que se puede actuar son las de Selección y Simulación:
-
Selección: existen varias mejoras posibles, como ser:
-
"Progressive Bias"[8]: Consiste en guiar la búsqueda incorporando heurísticas en la etapa de Selección, las cuales tendrán gran influencia cuando el número de simulaciones es menor y a medida que el número aumenta, su aporte disminuirá hasta ser nulo.
-
"Progressive Widening"[8]: consiste en podar el árbol en relación al tiempo disponible y número de simulaciones realizadas, con el objetivo de reducir el factor de crecimiento y concentrar la búsqueda en las mejores opciones encontradas hasta el momento.
-
-
Simulación:
En el enfoque inicial para las simulaciones, los movimientos a realizar en cada instante de juego se eligen de manera uniformemente aleatoria.
Sin embargo, este tipo de simulaciones resulta en partidas sin mucho sentido, perdiendo utilidad a la hora de evaluar un movimiento. La idea intuitiva es que las simulaciones deben ser los más cercanas a un juego de la realidad, de manera de poder evaluar con cierta seguridad como proseguiría el juego si se realizan determinados movimientos iniciales.
Entonces, resulta un desafío lograr un correcto balance entre exploración y explotación. Las simulaciones no deben ser demasiado aleatorias, ya que llevarían a resultados sin mucho sentido, ni demasiado deterministas, ya que perderían un gran rango de posibilidades/rumbos que tome el juego.
Para lograr esto, dentro de la documentación propia del área, se encontraron 2 principales enfoques:
-
"Urgency-based simulation"(Bouzy [6]): En cada instante de la simulación, un valor de urgencia U_j es computado para cada movimiento j posible, combinando un valor "capture-escape" (que considera el número de fichas que serían capturadas y el número que lograrían escapar de una captura, con dicho movimiento) con un valor que se calcula buscando ciertos patrones de 3x3 en el tablero. Luego, cada movimiento será elegido con mayor o menor probabilidad de acuerdo a su valor de urgencia U_j.
-
"Sequence-like simulation"(Gelly [9]): Consiste en seleccionar ciertos movimientos de interés en un área cercana al último movimiento realizado, resultando en una secuencia de movimientos cercanos uno del otro.
Para seleccionar un movimiento, se buscan respuestas locales a través de patrones. Estos patrones, son matrices de 3x3, centradas sobre una intersección libre (que representa el próximo movimiento a realizar) y intentan dar respuestas a algunas situaciones clásicas del juego Go. Son considerados únicamente en el perímetro alrededor del último movimiento realizado.
La idea detrás de este enfoque es:
-
Probablemente, movimientos cercanos serán la respuesta apropiada para contrarrestar los últimos movimientos realizados.
-
Es más importante obtener mejores secuencias de movimientos que mejores movimientos aislados.
-
-
A pesar de encontrar varios enfoques para introducir conocimiento, no resulta claro cómo evaluar cual es mejor sin hacer pruebas uno mismo con cada uno de ellos. Probablemente, el mejor resultado se logre a partir de una combinación de diferentes enfoques.
Sin embargo, debido al tiempo limitado con el que se cuenta, se decidió inclinarse por un enfoque en particular, mejorando la etapa de Simulación a través del uso de secuencias de movimientos, porque:
-
No requiere un gran gasto computacional como es el caso de calcular valores de urgencia para todos los movimientos en cada instante de simulación.
-
Es bastante simple de implementar.
-
Es el enfoque utilizado en MoGo[9], el cual logró muy buenos resultados siendo uno de los programas pioneros en el área.
Esta mejora se implementó a nuestro algoritmo de MCTS de la siguiente manera:
-
Incorporando una nueva clase SimulationWithDomainKnowledge que hereda de la clase Simulation y implementa el algoritmo para la selección del paso a realizar en cada instante de la simulación.
-
Creando una clase PatternList, que leerá una lista de patrones de un archivo y permitirá determinar si una posición matchea un patrón en un estado en particular:
class PatternList { ... //Determina si la posición (i,j) en el estado state, //``matchea" alguno de los patrones introducidos. bool match(StateGo *state,INDEX i,INDEX j); //Lee una lista de patrones del archivo ``file_name". read_file(String file_name); };Debido a que trabajamos con patrones de un tamaño menor, de 3x3, se logra implementar el algoritmo de manera de poder hacer el chequeo en tiempo constante. Básicamente:
-
Se crea un arreglo de 3^9=19683 booleanos, representando cada posición una posible combinación de un tablero de 3x3 y se lo inicializa en false.
-
Por cada patrón leído del archivo (dado en un formato general definido) se generan todos los posibles tableros 3x3 que coincidirán con dicho patrón, incluyendo simetrías y rotaciones. Por cada uno, se activa su posición en el arreglo, almacenando el valor true.
-
Luego, para saber si una posición matchea algún patrón, solo debo chequear que su posición en el arreglo tenga el valor true. Es decir, podemos hacerlo en tiempo constante O(1).
-
Los patrones utilizados en nuestras pruebas, fueron tomados de [10], y corresponden a varias situaciones clásicas del juego Go. Por ejemplo:
Además de las posiciones que concuerdan con patrones, otras posiciones resultan de gran importancia en el juego, las posiciones que determinan cuándo los bloques son capturados.
Por lo tanto, se incorporan algoritmos para detectar los movimientos de "Captura", es decir, los que permiten capturar bloques del oponente y los movimientos "Escape de atari", que permite aumentar el número de adyacencias de un bloque propio en estado de atari (una sola intersección libre y por lo tanto propenso a ser capturado por el oponente). Por ejemplo:
Posiciones de escape de atari a través de una captura de un bloque opuesto. La posición azul significará una captura de blancas y escape de atari del bloque negro principal, que pasará a tener dos adyacencias libres. De igual manera la posición roja para las fichas blancas.
Posición de escape de atari. La posición remarcada permite aumentar el número de adyacencias del bloque negro librándolo del peligro de ser capturado.
Fue necesario modificar el algoritmo de simulación para reemplazar la elección de movimientos puramente aleatorios por una elección que dé mayor importancia a las posiciones antes mencionadas.
Para elegir qué movimiento tomar en cada instante de la simulación, basándose en las propuestas presentadas en [11] y [7], se probaron diferentes variantes y finalmente se concluyó con el siguiente algoritmo (se muestra una versión simplificada):
list = []
Por cada movimiento de ESCAPE DE ATARI Mi que salva al bloque Bi,
incorporar size(Bi) veces Mi a list y si Mi además captura un
bloque enemigo Ei, incorporarlo size(Ei) veces más.
Si size(list) < CTE:
Intentar encontrar aleatoriamente una posición "FILL BOARD".
Si no se encuentra:
Incorporar a list toda posición adyacente (8-adj) al último
movimiento que concuerde con algún PATRÓN.
Por cada movimiento Mi de CAPTURA al bloque Bi, incorporarlo
a list size(Bi) veces.
Si list está vacía:
Incorporar a list todos los movimientos posibles.
Elegir, de forma uniformemente aleatoria, una posición de list
y realizar dicho movimiento.
De esta manera, incrementamos la probabilidad en que son elegidos los movimientos de mayor importancia. Es decir, un movimiento que me permite evitar que un bloque de tamaño 10 sea capturado, probablemente será mucho más importante que un movimiento que concuerda con un patrón, o uno que solo captura un bloque de tamaño 1. A la vez, si tenemos dos movimientos que nos permiten escapar de una situación de atari, probablemente nos interese más el que a la vez captura fichas del contrincante.
Sin embargo, aún si ponderamos la probabilidad de elegir ciertos movimientos, no anulamos el resto, de manera de asegurarnos cierta aleatoriedad en las simulaciones que nos permitan obtener una estimación más abarcativa del rumbo que pueda tomar el juego.
Cuando mencionamos una posición "fill board", nos referimos a la mejora mencionada en [11], que nos permite considerar ciertos movimientos en áreas no exploradas del tablero.
Intentando mejorar el número de simulaciones realizadas por tiempo, se analizaron diferentes optimizaciones sobre la clase StateGo. En cierto punto, se hizo evidente un cuello de botella en el proceso de obtener la lista de movimientos posibles en cada instante de juego. Para esto, se recorría toda la matriz del juego, buscando posiciones libres, que no impliquen suicidios ni otras restricciones de juego (como ser Ko). Esto nos llevaba a un costo fijo en cada iteración de la simulación.
Para evitar este costo, se propuso llevar un registro de los movimientos disponibles en cada instante de juego. Las principales operaciones sobre este conjunto serían:
-
Insertar un movimiento.
-
Eliminar un movimiento.
-
Obtener el número de movimientos disponibles.
-
Acceder al movimiento ubicado en la posición i.
Los dos últimos puntos se deben a que necesitamos elegir un movimiento aleatoriamente, y para esto tenemos que poder enumerarlos y acceder a ellos una vez elegido un número aleatorio dentro del conjunto.
Sin embargo, de las estructuras esenciales disponibles, no se contaba con ninguna que nos permita realizar todas las operaciones en una complejidad aceptable. Por ejemplo, se analizaron:
-
List: para insertar o eliminar un elemento de manera única, tendremos un costo lineal, al igual que para obtener el elemento i-ésimo.
-
Vector: nos permite obtener el elemento i-ésimo en tiempo constante. Pero insertar y eliminar elementos de manera única tendrá un costo lineal.
-
Set: nos permite insertar y eliminar elementos en tiempo log(n), pero acceder al elemento i-ésimo tendrá un costo lineal. Es decir, se permite un acceso secuencial y no aleatorio a los elementos.
Por lo tanto, se decidió implementar una nueva estructura que nos permita realizar las 3 operaciones en una complejidad aceptable. Se comenzó con un árbol binario AVL [12], continuamente balanceado, que nos asegura complejidad log(n) para inserción y eliminación de elementos.
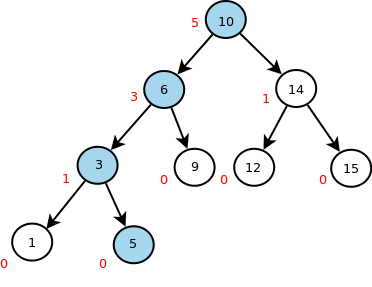
Para permitir acceso aleatorio a los elementos, se decidió incorporar una modificación sobre el árbol, donde cada nodo lleva un registro del número de elementos en el sub árbol izquierdo, es decir, el sub árbol que contiene los elementos menores. Esta modificación incorpora gastos mínimos en la actualización del árbol, pero nos permite buscar el elemento i-ésimo con una complejidad log(n).
Ejemplo de una búsqueda del elemento en la posición 2. Número rojos representan el número de nodos en el subárbol a izquierda de cada nodo.
Dentro de la implementación del programa hay varias variables que se pueden modificar e influyen en la forma que el programa progresa, como ser: la lista de patrones a utilizar, el coeficiente de exploración para el algoritmo UCT, la variable K del algoritmo RAVE, el número de intentos de llenar el tablero en una simulación, el número de visitas antes de expandir un nodo, el número de ciclos del algoritmo que se realizarán antes de cada movimiento, el número de threads a utilizar en paralelo, etc.
De manera de poder testear al programa en diferentes situaciones y así buscar los valores óptimos para cada una de estas variables, se implementaron varias opciones de linea de comando que permiten configurar cada una de ellas sin necesidad de recompilar el código (en caso de no estar presentes, se toma un valor por defecto).
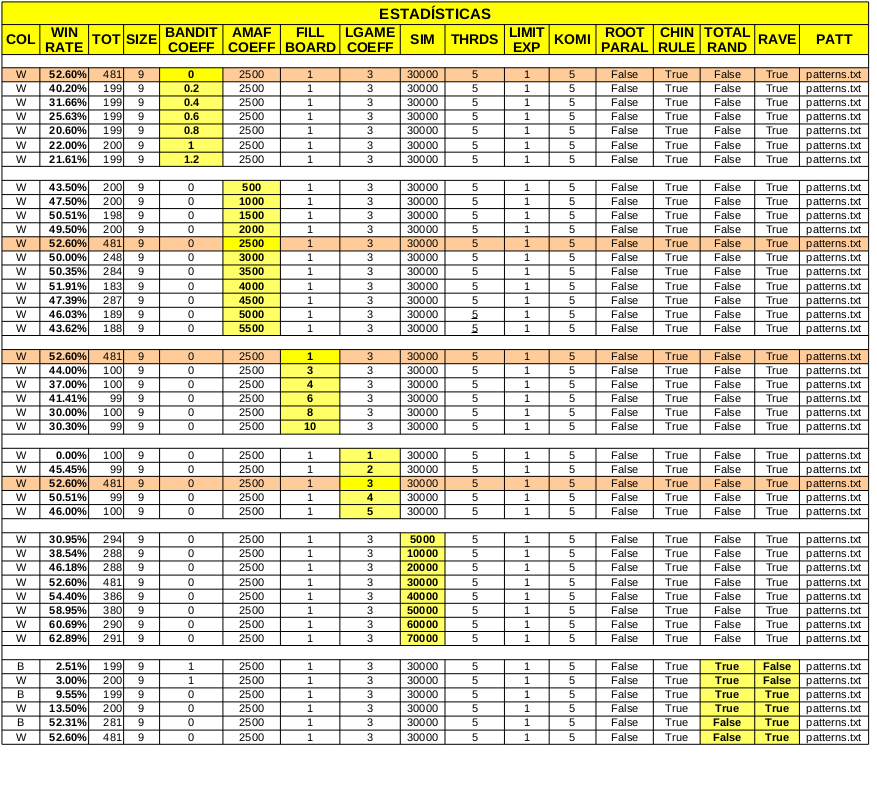
Haciendo uso de estas opciones, de la aplicación "gogui-twogtp"[14] que permite correr múltiples partidas entre dos programas y de un script que se creó para generar estadísticas ("generate_stats.py"), se testeó al programa corriendo múltiples partidas modificando el valor de diferentes variables y analizando el porcentaje de partidas ganadas. En el Apéndice se pueden encontrar los datos exactos de las estadísticas realizadas.
 Análisis del coeficiente de
exploración.
Análisis del coeficiente de
exploración.
De acuerdo a las pruebas realizadas para diferentes valores del coeficiente de exploración en el algoritmo UCT, y en concordancia con los resultados presentados en [2], el valor óptimo luego de la incorporación de la mejora RAVE, resulta ser 0.
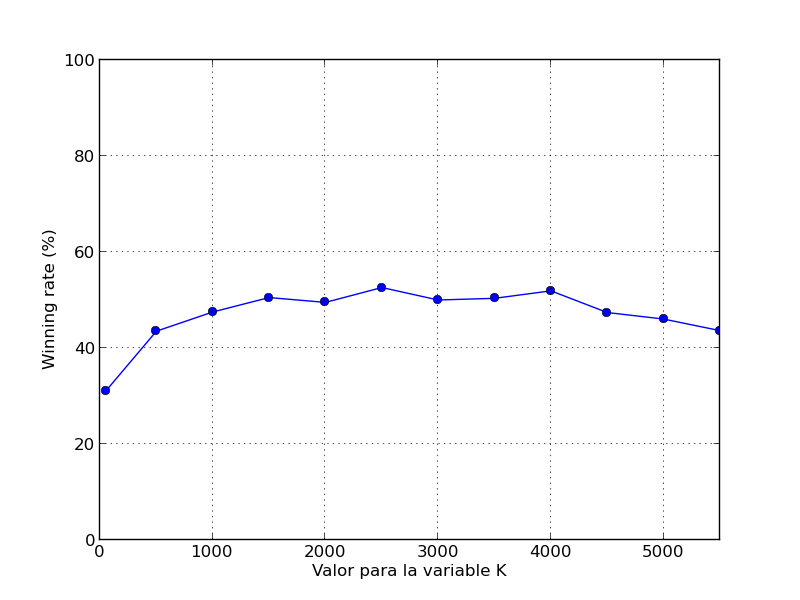 Análisis del coeficiente K de
selección Rave.
Análisis del coeficiente K de
selección Rave.
De acuerdo a las pruebas realizadas para diferentes valores del coeficiente K (que determina cómo varía el peso de la heurística amaf con respecto a la tasa de éxito a medida que aumenta el número de simulaciones en el algoritmo UCT-RAVE) el valor óptimo resulta ser 2500.
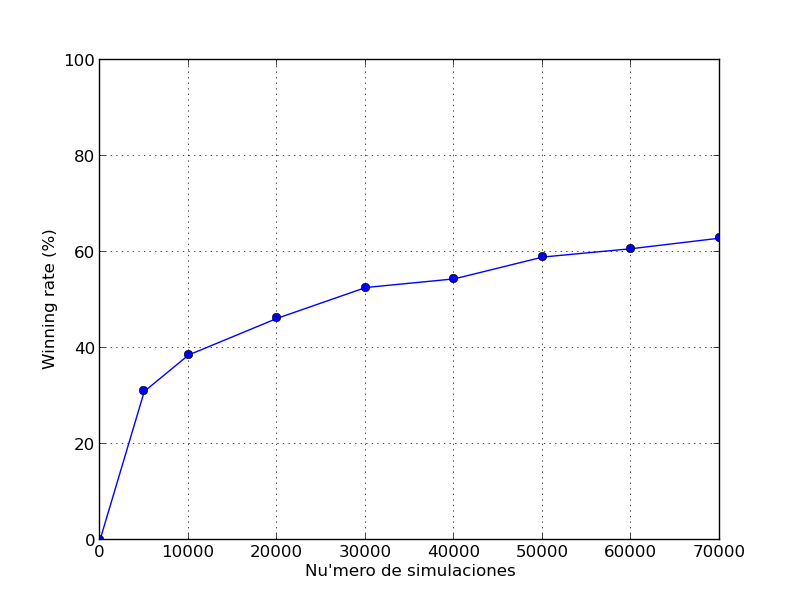 Análisis del número de simulaciones.
Análisis del número de simulaciones.
Claramente, aumentar el número de simulaciones incrementará el porcentaje de partidas ganadas, porque más simulaciones nos permite tener un árbol cada vez más grande y más cercano al árbol min-max completo.
Sin embargo, con cada incremento en el número de simulaciones directamente tendremos un aumento en el tiempo necesario para cada toma de decisiones.
En nuestro caso se lograron buenos resultados con 30000 simulaciones por mov. Ejecutando el algoritmo sobre 5 threads en paralelo, en una máquina de 4 cores, requiere aproximadamente 2 segundos por movimiento.
Las siguientes estadísticas se realizaron sobre un tablero de 9x9, utilizando la puntuación China (por Área) y un komi de 5 puntos.
-
Estadísticas sobre 100 partidas entre el programa, con simple UCT, y el mismo con la incorporación de la mejora RAVE (30000 sim. por mov.):
Programa 1 Programa 2 Blanco/Negro % Ganado Prog1 UCTRave Aleatorio UCT Aleatorio Blanco 100% UCTRave Aleatorio UCT Aleatorio Negro 100%
-
Estadísticas sobre 100 partidas entre el programa, con simulaciones totalmente aleatorias, y el mismo con la incorporación de patrones y valores de capturas (30000 sim. por mov.):
Programa 1 Programa 2 Blanco/Negro % Ganado Prog1 UCTRave con Conoc. Dominio UCTRave Aleatorio Blanco 93% UCTRave con Conoc. Dominio UCTRave Aleatorio Negro 94%
-
Estadísticas sobre 500 partidas contra GnuGo-3.8 level 10[13] (30000 sim. por mov.):
Programa Blanco/Negro % Ganado UCT Aleatorio Blanco 5% UCT Aleatorio Negro 3% UCTRave Aleatorio Blanco 14% UCTRave Aleatorio Negro 8% UCTRave con Conoc. Dominio Blanco 52% UCTRave con Conoc. Dominio Negro 51%
-
Incorporar conocimiento de dominio en la etapa de Selección, por ejemplo implementando "Progressive Bias"[8] o "Progressive Widening"[8].
-
Probar el programa con nuevos patrones e investigar la posibilidad de aprender dichos patrones automáticamente. Algunos resultados sobre intentos de aprendizaje automatizado, se pueden encontrar en [8].
-
Mejorar el programa para que pueda regular el tiempo automáticamente de acuerdo a la etapa en la que se encuentre del juego. (Es decir, poder evaluar cuándo tiene sentido invertir más tiempo explorando y cuándo no es necesario). También se podría mejorar el programa de manera que continue procesando mientras el oponente decide qué movimiento realizar.
-
Mejorar la evaluación del tablero de juego de manera de poder determinar cuándo un bloque está muerto. Un bloque muerto es un bloque que no tiene posibilidades de sobrevivir si el oponente juega adecuadamente.
Esto resulta muy importante si consideramos la puntuación japonesa. Cuando un jugador incorpora fichas en un territorio del contrincante y no tienen posibilidades de sobrevivir, entonces esas fichas se consideran muertas y directamente no se intentan capturar, ya que hacerlo haría perder puntaje (muchas veces para capturar un bloque es necesario poner mas fichas que el tamaño del bloque y por lo tanto al capturarlo terminamos perdiendo mas puntaje que si no lo hacemos.) Sin embargo, la noción de bloque muerto no es simple de implementar y esto lleva a problemas cuando queremos evaluar nuestro programa contra otros programas utilizando esta puntuación. Como nuestro programa no reconoce bloques muertos, intentará introducir fichas en el territorio contrario de manera de que el contrincante se vea obligado a capturarlas y pierda puntos. Pero, muchos programas como GnuGo detectan esto y directamente no capturan dichos bloques. Esto lleva a una diferencia significativa en el puntaje que considera cada programa al finalizar el juego y muchas veces difieren respecto al ganador.
En la puntuación china, no tenemos este problema, pues las fichas sobre el tablero tienen el mismo valor que las posiciones de territorio ganadas, por lo tanto, introducir nuevas fichas para capturar un bloque no nos llevarán a la perdida de puntos.
-
Incorporar más optimizaciones a la clase StateGo y el algoritmo de simulación.
-
Analizar y optimizar el programa para tamaños de tablero distintos de 9x9, como ser 13x13 y 19x19. Estas opciones no se analizaron detenidamente en nuestro caso y pueden requerir cambios en los algoritmos de simulación y criterios de las demás etapas para lograr un jugador de un nivel aceptable.
-
Implementar la etapa de simulación utilizando GPGPU. De esta manera se podrían realizar muchísimas más simulaciones en igual tiempo y definitivamente la eficiencia del programa aumentaría con mayor porcentaje de partidas ganadas. Investigación en este tema se puede encontrar en [17] y [18].
Bibliografía:
[1] Beatriz Nasarre Embid. Método de Monte-Carlo Tree Search (MCTS) para
resolver problemas de alta complejidad: Jugador virtual para el juego
del Go.
http://zaguan.unizar.es/TAZ/EINA/2012/8010/TAZ-PFC-2012-393.pdf
[2] Sylvain Gelly and David Silver. 2011. Monte-Carlo Tree Search and
Rapid Action Value Estimation in Computer Go. Artif. Intell. 175, 11
(July 2011), 1856-1875.
http://www0.cs.ucl.ac.uk/staff/D.Silver/web/Applications_files/mcrave.pdf
[3] Guillaume M.J-B. Chaslot, Mark H.M. Winands, and H. Jaap van den
Herik. Parallel Monte-Carlo Tree Search.
https://dke.maastrichtuniversity.nl/m.winands/documents/multithreadedMCTS2.pdf
[4] Levente Kocsis and Csaba Szepesvári. Bandit based Monte-Carlo
Planning.
http://www.sztaki.hu/~szcsaba/papers/ecml06.pdf
[5] Bruno Bouzy. Associating domain-dependent knowledge and Monte Carlo
approaches within a go program.
http://www.math-info.univ-paris5.fr/~bouzy/publications/Bouzy-InformationSciences.pdf
[6] Guillaume Maurice Jean-Bernard Chaslot. Monte-Carlo Tree Search.
https://project.dke.maastrichtuniversity.nl/games/files/phd/Chaslot_thesis.pdf
[7] Guillaume Chaslot, Louis Chatriot, C. Fiter, Sylvain Gelly,
Jean-Baptiste Hoock, Julien Perez, Arpad Rimmel, Olivier Teytaud.
Combining expert, offline, transient and online knowledge in Monte-Carlo
exploration.
https://www.lri.fr/~teytaud/eg.pdf
[8] Guillaume Chaslot, Mark H.M. Winands, H. Jaap van den Herik, Jos
W.H.M. Uiterwijk, Bruno Bouzy. Progressive Strategies for Monte-Carlo
tree search.
https://gnunet.org/sites/default/files/NMNC%20-%20Progressive%20strategies%20for%20MCTS.pdf
[9] Sylvain Gelly, Yizao Wang, Modifications of UCT and sequence-like
simulations for Monte-Carlo Go.
http://dept.stat.lsa.umich.edu/~yizwang/publications/wang07modifications.pdf
[10] Sylvain Gelly, Yizao Wang, Rémi Munos, Olivier Teytaud. Modification
of UCT with Patterns in Monte-Carlo Go.
https://hal.inria.fr/inria-00117266/PDF/RR-6062.pdf
[11] Chang-Shing Lee, Mei-Hui Wang, Guillaume Chaslot, Jean-Baptiste
Hoock, Arpad Rimmel. The Computational Intelligence of MoGo Revealed in
Taiwan’s Computer Go Tournaments.
https://hal.archives-ouvertes.fr/file/index/docid/369786/filename/TCIAIG-2008-0010_Accepted_.pdf
[12] Georgy Adelson-Velsky, G.; E. M. Landis (1962). ``An algorithm for the organization of information". Proceedings of the USSR Academy of Sciences 146: 263–266. (Russian) English translation by Myron J. Ricci in Soviet Math. Doklady, 3:1259–1263, 1962.
[13] GNU Go. https://www.gnu.org/software/gnugo/
[14] GoGui. http://gogui.sourceforge.net/
[15] Go Text Protocol.
http://www.gnu.org/software/gnugo/gnugo_19.html
[16] Monte Carlo Tree Search (MCTS) research hub.
http://mcts.ai
[17] Kamil Marek Rocki, Reiji Suda, ``Large Scale Monte Carlo Tree
Search on GPU".
http://olab.is.s.u-tokyo.ac.jp/~kamil.rocki/phd_thesis.pdf
[18] Zhou, J. (2013). Parallel Go on CUDA with Monte Carlo Tree Search.
(Electronic Thesis or Dissertation).
https://etd.ohiolink.edu/ap:10:0::NO:10:P10_ETD_SUBID:4810#abstract-files