Syntactic analysis toolkit, language agnostic parsers generator.
Implements LR and LL parsing algorithms.
You can get an introductory overview of the tool in this article.
- Installation
- Development
- CLI usage example
- Parser generation
- Language agnostic parser generator
- Grammar format
- Lexical grammar and tokenizer
- Working with precedence and associativity
- Handler arguments notation
- Capture location objects
- Parsing modes
- Validating grammar
- Module include, and parser events
- Debug mode
The tool can be installed as an npm module (notice, it's called syntax-cli there):
npm install -g syntax-cli
syntax-cli --help
- Fork the https://github.com/DmitrySoshnikov/syntax repo
- Make your changes
- Make sure
npm testpasses (add new tests if needed) - Submit a PR
NOTE: If you need to implement a Syntax plugin for a new target programming language, address this instruction.
For development from the github repository, run build command to transpile ES6 code:
git clone https://github.com/<your-github-account>/syntax.git
cd syntax
npm install
npm run build
./bin/syntax --help
Or for faster development cycle, one can also use watch command (notice though, it doesn't copy template files, but only transpiles ES6 code; for templates copying you have to use build command):
npm run watch
./bin/syntax --grammar examples/grammar.lr0 --parse "aabb" --mode lr0 --table --collection
To generate a parser module, specify the --output option, which is a path to the output parser file. Once generated, the module can normally be required, and used for parsing strings based on a given grammar.
Example for the JSON grammar:
./bin/syntax --grammar examples/json.ast.js --mode SLR1 --output json-parser.js
✓ Successfully generated: json-parser.js
Loading as a JS module:
const JSONParser = require('./json-parser');
let value = JSONParser.parse('{"x": 10, "y": [1, 2]}');
console.log(value); // JS object: {x: 10, y: [1, 2]}See this instruction how to implement a new plugin.
Syntax is language agnostic when it comes to parser generation. The same grammar can be used for parser generation in different languages. Currently Syntax supports JavaScript, Python, PHP, Ruby, C#, and Rust. The target language is determined by the output file extension.
For example, this is how to use the same calculator grammar example to generate parser module in Python:
./bin/syntax -g examples/calc.py.g -m lalr1 -o calcparser.py
The calcparser module then can be required normally in Python for parsing:
>>> import calcparser
>>> calcparser.parse('2 + 2 * 2')
>>> 6Another example shows how to use parser hooks (such as on_parse_begin, on_parse_end, and other) in Python. They are discussed below in the module include section.
For PHP the procedure is pretty much the same, take a look at the similar example:
./bin/syntax -g examples/calc.php.g -m lalr1 -o CalcParser.php
The output file contains the class name corresponding to the file name:
<?php
require('CalcParser.php');
var_dump(CalcParser::parse('2 + 2 * 2')); // int(6)The parser hooks for PHP can be found in this example.
Ruby is another target language supported by Syntax. Its calculator example is very similar:
./bin/syntax -g examples/calc.rb.g -m lalr1 -o CalcParser.rb
And also the output file contains the class name corresponding to the file name:
require 'CalcParser.php'
puts CalcParser.parse('2 + 2 * 2') // 6Ruby's parsing hooks can be found in the following example.
Syntax supports as well C# as a target language. See its calculator example:
./bin/syntax -g examples/calc.cs.g -m lalr1 -o CalcParser.cs
Then callers can use the module as:
using SyntaxParser;
...
var parser = new CalcParser();
Console.WriteLine(parser.parse("2 + 2 * 2")); // 6Parsing hooks example in C# format can be found in this example.
Rust is a system programming language focusing on efficiency and memory safety. Syntax has support for generating parsers in Rust. See the simple example, and an example of generating an AST with recursive structures.
./bin/syntax -g examples/calc.rs.g -m lalr1 -o lib.rs
Callers can create a crate (called syntax in the example below), which contains the parser, and use it as:
extern crate syntax;
use syntax::Parser;
fn main() {
let mut parser = Parser::new();
let result = parser.parse("2 + 2 * 2");
println!("{:?}", result); // 6
}Check out README file from rust directory for more information.
Syntax support two main notations to define grammars: JSON-like notation, and Yacc/Bison-style notation.
JSON-"like" is because it's excented JSON notation, and may include any JavaScript syntax (e.g. quotes may be omitted for properties, can use comments, etc):
/**
* Basic calculator grammar in JSON notation.
*/
{
// ---------------------------
// Lexical grammar.
lex: {
rules: [
[`\\s+`, `/* skip whitespace */`],
[`\\d+`, `return 'NUMBER'`],
[`\\+`, `return '+'`],
[`\\*`, `return '*'`],
[`\\(`, `return '('`],
[`\\)`, `return ')'`],
],
},
// ---------------------------
// Operators precedence.
operators: [
[`left`, `+`],
[`left`, `*`],
],
// ---------------------------
// Syntactic grammar.
bnf: {
e: [[`e + e`, `$$ = $1 + $3`],
[`e * e`, `$$ = $1 * $3`],
[`( e )`, `$$ = $2`],
[`NUMBER` `$$ = Number($1)`]],
}
}As we can see, lex defines lexical grammar, bnf provides syntactic grammar, and operators may defines associativity and precedence of needed symbols. List of available grammar properties is specified below.
And here is the same grammar in the Yacc/Bison format:
/**
* Basic calculator grammar in Yacc/Bison notation.
*/
%lex
%%
\s+ /* skip whitespace */
\d+ return 'NUMBER'
/lex
%left '+'
%left '*'
%%
e
: e '+' e { $$ = $1 + $3 }
| e '*' e { $$ = $1 + $3 }
| '(' e ')' { $$ = $2 }
| NUMBER { $$ = Number($1) }
;
Simple tokens like '+' can be defined inline (with quotes), and complex tokens like NUMBER has to be defined in the lexical grammar. Lexical and syntactic grammars can also be defined in two separate files.
A grammar in Yacc/Bison format is also just parsed by Syntax using our BNF parser. The resulting parsed AST corresponds exactly to the JSON-like notation described above.
Below is the list of available grammar properties.
lex- lexical grammar.bnf- syntactic grammar in BNF format.operators- associativity and precedence of needed grammar symbols (usually operators, but not necessarily). Can be used to resolve "shift-reduce" conflicts in cases like "dangling-else" problem, math-operators, etc.moduleInclude-- the code which is included "as is" into the generated parser module. Usually used to require or define inline classes for AST nodes, and any additional code.startSymbol- starting symbol (if not specified, it's inferred from the LHS of the first rule).tokens- explicit list of tokens (if not specified, it's automatically inferred from the grammar).
Tokenizers use formalism of regular grammars in order to split a string into a list of tokens. One of the convenient implementations of the regular grammars is regular expressions.
A basic format of a lexical grammar should provide at least rules section:
{
rules: [
[`\\d+`, `return 'NUMBER'`],
[`"[^"]*"`, `yytext = yytext.slice(1, -1); return 'STRING';`],
...
],
}The first element of a lexical rule is the regexp pattern to match, and the second element is the corresponding token handler, which should return type of the matched token.
Handlers may access the matched text as yytext variable, which is also can be mutated -- in the example above for the STRING token we modify matched text to be the quoted value, stripping the quotes themselves.
A handler can be arbitrary complex function, and in addition may return multiple tokens, using an array (see also this example):
// Return 3 tokens for one matched value.
return ['DEDENT', 'DEDENT', 'NL'];
Lexical grammar may also define macros field -- variables which can be used later in rules, and also start conditions for tokenizer states, which are discussed below.
{
macros: {
id: `[a-zA-Z0-9_]`,
},
rules: [
[`{id}+`, `return 'IDENTIFIER'`],
...
],
}It is possible to analyze just a list of tokens either from the lex part of the --grammar, or from a standalone --lex file.
Example:
// ~/lang.lex
{
rules: [
[`\\s+`, `/* skip whitespace */`],
[`\\d+`, `return 'NUMBER'`],
[`(\\+|\\-)`, `return 'ADDITIVE_OPERATOR'`],
],
}Extract the tokens:
./bin/syntax --lex ~/lang.lex --tokenize -p '2 + 5'
The result:
[
{
"type": "NUMBER",
"value": "2",
"startOffset": 0,
"endOffset": 1,
"startLine": 1,
"endLine": 1,
"startColumn": 0,
"endColumn": 1
},
{
"type": "ADDITIVE_OPERATOR",
"value": "+",
"startOffset": 2,
"endOffset": 3,
"startLine": 1,
"endLine": 1,
"startColumn": 2,
"endColumn": 3
},
{
"type": "NUMBER",
"value": "5",
"startOffset": 4,
"endOffset": 5,
"startLine": 1,
"endLine": 1,
"startColumn": 4,
"endColumn": 5
}
]As you can see, along with the type, and the value, a tokenizer also captures token locations: absolute offsets, line, and column numbers.
NOTE: built-in tokenizer uses underlying regexp implementation to extract stream of tokens.
It is possible to provide a custom tokenizer if a built-in isn't sufficient. For this pass the --custom-tokenizer option, which is a path to a file that implements a tokenizer. In this case the built-in tokenizer code won't be generated.
./bin/syntax --grammar examples/json.ast.js --mode SLR1 --output json-parser.js --custom-tokenizer './my-tokenizer.js'
✓ Successfully generated: json-parser.js
In the generated code, the custom tokenizer is just required as a module: require('./my-tokenizer.js').
The tokenizer should implement the following iterator-like interface:
initString: initializes a parsing string;hasMoreTokens: whether stream of tokens still has more tokens to consume;getNextToken: returns next token in the format{type, value};
For example:
// File: ./my-tokenizer.js
const MyTokenizer = {
initString(string) {
this._string = string;
this._cursor = 0;
},
hasMoreTokens() {
return this._cursor < this._string.length;
},
getNextToken() {
// Implement logic here.
return {
// Basic data.
type: <<TOKEN_TYPE>>,
value: <<TOKEN_VALUE>>,
// Location data.
startOffset: <<START_OFFSET>>,
endOffset: <<END_OFFSET>>,
startLine: <<START_LINE>>,
endLine: <<END_LINE>>,
startColumn: <<START_COLUMN>>,
endColumn: <<END_COLUMN>>,
}
},
};
module.exports = MyTokenizer;Built-in tokenizer supports stateful tokenization. This means the same lex rule can be applied in different states, and result to a different token. For lex rules it's known as start conditions.
Rules with explicit start conditions are executed only when lexer enters the state corresponding to their names. Start conditions can be inclusive (%s, 0), and exclusive (%x, 1). Inclusive conditions also include rules without any start conditions, and exclusive conditions do not include other rules when the parser enter their state. The rules with * start condition are always included.
"lex": {
"startConditions": {
"comment": 1, // exclusive
"string": 1 // exclusive
},
"rules": [
...
// On `/*` enter `comment` state:
["\\/\\*", "this.pushState('comment');"],
// The rule is executed only when tokenizers enters `comment`, or `string` state:
[["comment", "string"], "\\n", "lines++; return 'NL';"],
...
],
}More information on the topic can be found in this gist.
As an example take a look at this example grammar, which calculates line numbers in a source file, including line numbers in comments. The comments themselves are skipped during tokenization, however the new lines are handled within comments separately to count those line numbers as well.
Another example is the grammar for BNF itself, which we use to parse BNF grammars represented as strings, rather than in JSON format. There we have action start condition to correctly parse { and } of JS code, being inside an actual handler for a grammar rule, which is itself surrounded by { and } braces.
It is also possible to access tokenizer instance from the parser semantic actions. It is exposed via the yy.lexer object (yy.tokenizer is an alias).
Having access to the lexer, it is possible, for example, to change its state, and yield different token types for the same characters.
As an example, differently parsing { and } being in an expression or in a statement position in ECMAScript language:
{x: 1} // BlockStatement
({x: 1}) // ObjectLiteral
A simplified example for this can be found in the parser-lexer-communication.g grammar example.
Lexical grammar rules can also be case-insensitive. From the command line it's control via the appropriate --case-insensitive (-i) option. It also can be specified in the lexical grammar itself -- for the whole grammar, or per each rule:
// case-insensitive.lex
{
"rules": [
// This rule is by default case-insensitive:
[`x`, `return "X"`],
// This rule overrides global options:
[`y`, `return "Y"`, {"case-insensitive": false}],
],
// Global options for the whole lexical grammar.
"options": {
"case-insensitive": true,
},
}See this example for details.
Precedence and associativity operators allow building more readable and elegant grammars, avoiding different kinds of conflicts, like "shift-reduce" conflicts.
Supported precedence operators are:
%left-- left-associative;%right-- right-associative;%nonassoc-- non-associative.
Having the following snippet from the calculator grammar:
%%
e
: e '+' e
| e '*' e
| '(' e ')'
| NUMBER
;
we get a "shift-reduce" conflict for the input like:
2 + 2 + 2
Once have parsed the first 2 + 2, and having + as the lookahead, the parser cannot decide, whether it should reduce the parsed 2 + 2 value to e, or it should to shift further, since 2 itself can be e (by NUMBER rule), and parser can expect + after e.
Defining associativity for the + operator solves it easily and elegantly:
%left '+'
%left '*'
%%
e
: e '+' e
| e '*' e
| '(' e ')'
| NUMBER
;
Here by %left '+' we say that + is left-associative, which means that parser should parse 2 + 2 + 2 as (2 + 2) + 2, and not as 2 + (2 + 2). In other words, once the parser have parsed 2 + 2, and still sees + as the lookahead, it chooses to reduce instead of shift, and "shift-reduce" conflict is resolved.
Another example is having the snippet as:
2 + 2 * 2
If parser would reduce in this case, we would get an invalid mathematical expression, since this expression, without any grouping parenthesis, should be parsed as 2 + (2 * 2), and not as (2 + 2) * 2.
To solve this we use %left '*' which in our grammar definition stays in order after the %left '+', which makes the * operator to have a higher precedence, than the + has. In this case parser chooses to shift further instead of reducing.
Note, from JSON-like notation they are defined as:
operators: [
['left', '+'],
['left', '*'],
// etc.
]Sometimes we don't need any associativity, but just want to specify precedence of some symbols. As a classic example, we can take the dangling-else problem, for which we use %nonassoc operator:
%nonassoc THEN
%nonassoc 'else'
%%
IfStatement
: 'if' '(' Expression ')' Statement %prec THEN
| 'if' '(' Expression ')' Statement 'else' Statement
;
As we can see, 'else' token has higher precedence again, since goes after ("virtual") THEN token, so there is no "shift-reduce" conflict in this case.
Here %prec is used in production to specify which precedence to apply, using the "virtual" THEN symbol -- in this case it's not a real token (in contrast with 'else'), but just precedence name in order to refer it from the production.
You can find this problem handled in this grammar example.
The following notation is used for semantic action (handler) arguments:
yytext-- a matched token valueyyleng-- the length of the matched token- Positioned arguments, e.g.
$1,$2, etc. - Positioned locations, e.g.
@1,@2, etc. - Named arguments, e.g.
$foo,$bar, etc. - Named locations, e.g.
@foo,@bar, etc. $$-- result value@$-- result location
This is the simplest notation -- the semantic action arguments can be accessed via their number. For example, for the production:
exp : exp '+' term { $$ = $1 + $3 }
The exp can be accessed as $1, the $2 would contain '+', and $3 corresponds to the term.
Sometimes using positioned arguments can be less readable, and may cause refactoring issues. E.g. if some symbol is removed from the production, the handler code should be updated:
exp : '+' exp term { $$ = $2 + $3 }
In this case using named arguments might be more suitable:
exp : exp '+' term { $$ = $exp + $term }
Still the same, even if the production is changed:
exp : '+' exp term { $$ = $exp + $term }
Notice though, that for duplicated symbols named notation doesn't work, since causes ambiguity:
exp : exp '+' exp { $$ = $exp + $exp } /* ERROR! */
In this case the positioned arguments should be used:
exp : exp '+' exp { $$ = $1 + $3 } /* OK! */
For some tools (e.g source-code transformation tools) it is important not only to produce AST nodes, but also to capture all the locations in the original source code. Syntax supports --loc option for this. A default structure of a location object is the same as for a token:
{
startOffset,
endOffset,
startLine,
endLine,
startColumn,
endColumn,
}However in actual AST nodes generation it is possible to build a custom location information based on this default location object.
The locations are accessed using @1, or @foo notation, the result location is in the @$:
exp : exp + exp
{
$$ = $1 + $2;
// Default algorithm.
@$.startLine = @1.startLine;
@$.endLine = @3.endLine;
@$.startColumn = @1.startColumn;
@$.endColumn = @3.endColumn;
...
}
By default Syntax automatically calculates resulting location taking start part from the first symbol of a production, and the end part -- from the last symbol of the production. So the example above can actually omit manual result location calculation, and be just:
exp : exp + exp { $$ = $1 + $2; }
It is possible to override though the default algorithm by just mutating the @$, and it's also possible to create a custom location:
exp : exp + exp { $$ = new AdditionNode($1, $3, Loc(@$)) }
In this case function Loc can create custom location format. Here is another example of a grammar which uses location objects.
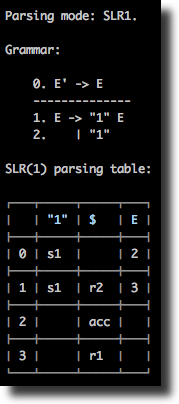
Syntax supports several LR parsing modes: LR(0), SLR(1), LALR(1), CLR(1) as well LL(1) mode. The same grammar can be analyzed in different modes, from the CLI it's controlled via the --mode option, e.g. --mode slr1.
Note: de facto standard for automatically generated parsers is usually the LALR(1) parser. The CLR(1) parser, being the most powerful, and able to parse wider grammar sets, can have much more states than LALR(1), and usually is suitable for educational purposes. As well as its less powerful counterparts, LR(0) and SLR(1) which are less used on practice (although, some production-ready grammars can also normally be parsed by SLR(1), e.g. JSON grammar).
Some grammars can be handled by one mode, but not by another. In this case a conflict will be shown in the table.
Currently an LL(1) grammar is supposed to be already left-factored, and to be non-left-recursive. See section on LL conflicts for details.
Note: left-recursion elimination, and left-factoring process can be automated for most of the cases (excluding some edge cases, which should be done manually), and implement a transformation to a non-left-recursive grammar.
A typical LL parsing table is less, than a corresponding LR-table. However, LR grammars cover more languages than LL grammars. In addition, an LL(1) grammar usually might look less elegant, or even less readable, than an LR grammar. As an example, take a look at the calculator grammar in the non-left-recursive LL mode, left-recursive LR mode, and also left-recursive, and precedence-based LR-mode.
At the moment, LL parser only implements syntax validation, not providing semantic actions (e.g. to construct an AST). For the semantic handlers, and actual AST construction see LR parsing.
LR parsing, and its the most practical version, the LALR(1), is widely used in automatically generated parsers. LR grammars usually look more readable, than corresponding LL grammars, since in contrast with the later, LR parser generators by default allow left-recursion, and do automatic conflict resolutions. The precedence and assoc operators allow building more elegant grammars with smaller parsing tables.
Take a look at the example grammar with a typical syntax-directed translation (SDT), using semantic actions for AST construction, direct evaluation, and any other transformation.
In LR parsing there are two main types of conflicts: "shift-reduce" (s/r) conflict, and "reduce-reduce" (r/r) conflict. Taking as an example grammar from examples/example1.slr1, we see that the parsing table is normally constructed for SLR(1) mode, but has a "shift-reduce" conflict if ran in the LR(0) mode:
./bin/syntax --grammar examples/example1.slr1 --table
./bin/syntax --grammar examples/example1.slr1 --table --mode lr0
Sometimes changing parsing mode is not enough for fixing conflicts: for some grammars conflicts may stay and in the LALR(1), and even the CLR(1) modes. LR conflicts can be resolved though automatically and semi-automatically by specifying precedence and associativity of operators.
For example, the following grammar has a shift-reduce conflict:
%token id
%%
E
: E '+' E
| E '*' E
| id
;
Therefore, a parsing is not possible using this grammar:
./bin/syntax -g examples/calculator-assoc-conflict.g -m lalr1 -w -p 'id * id + id'
Parsing mode: LALR(1).
Parsing: id * id + id
Rejected: Parse error: Found "shift-reduce" conflict at state 6, terminal '+'.
This can be fixed though using operators associativity and precedence:
%token id
%left '+'
%left '*'
%%
E
: E '+' E
| E '*' E
| id
;
See detailed description of the conflicts resolution algorithm in this example grammar, which is can be parsed normally:
./bin/syntax -g examples/calculator-assoc.g -m lalr1 -w -p 'id * id + id'
Parsing mode: LALR(1).
Parsing: id * id + id
✓ Accepted
By using --validate option, it is possible to check whether your grammar is free from different kinds of conflicts, and if it is not, to get needed information about which grammar rules conflict, and wich possible solutions can be applied to resolve them.
For example, discussed above calculator-assoc-conflict grammar has "shift-reduce" conflicts in two productions:
./bin/syntax -g examples/calculator-assoc-conflict.g -m slr1 --validate
Parsing mode: SLR(1).
Grammar has the following unresolved conflicts:
"Shift-reduce" conflicts:
1. Production: E -> E '+' E, conflicts with symbols '+', '*'.
2. Production: E -> E '*' E, conflicts with symbols '+', '*'.
Possible solutions:
1. Conflicts possibly can be resolved by using "operators" section,
where you can specify precedence and associativity.
2. By using different parsing mode, e.g. LALR1 instead of SLR1.
3. Restructuring grammar.
As we can see, Syntax showed which rules conflict with which lookahead symbols, and provided possible solutions.
In this case, rule E -> E '+' E conflicts with lookahead '+', and '*'. This means, that if have id + id + id, which would expand to E '+' E '+' E, the parser wouldn't know whether to reduce first E '+' E to E, or whether to shift further when it sees the second '+' symbol.
By specifying operators precedence, and associativity, we can resolve this conflict, which is done in the calculator-assoc grammar:
./bin/syntax -g examples/calculator-assoc.g -m slr1 --validate
Parsing mode: SLR(1).
✓ Grammar doesn't have any conflicts!
The moduleInclude directive allows injecting an arbitrary code to the generated parser file. This is usually code to require needed dependencies, or to define them inline. As an example, see the corresponding example grammar, which defines all classes for AST nodes inline, and then uses them in the rule handlers.
The code can also define handlers for some parse events (attaching them to yyparse object), in particular for onParseBegin and onParseEnd. This allow injecting a code which is executed when the parsing process starts, and ends accordingly.
"moduleInclude": `
class Node {
constructor(type) {
this.type = type;
}
}
class BinaryExpression extends Node {
...
}
// Event handlers.
yyparse.onParseBegin = (string) => {
console.log('Parsing code:', string);
};
yyparse.onParseEnd = (value) => {
console.log('Parsed value:', value);
};
`,
...
["E + E", "$$ = new BinaryExpression($1, $3, $2)"],Debug mode allows measuring timing of certain steps, and analyzing other debug information. From the CLI it's activated using --debug (-d) option:
./bin/syntax -g examples/calc-eval.g -m slr1 -p '2 + 2 * 2' --debug
DEBUG mode is: ON
[DEBUG] Grammar (bnf) is in JS format
[DEBUG] Grammar loaded in: 2.255ms
Parsing mode: SLR(1).
Parsing:
2 + 2 * 2
[DEBUG] Building canonical collection: 15.219ms
[DEBUG] Number of states in the collection: 22
[DEBUG] Building LR parsing table: 4.169ms
[DEBUG] LR parsing: 2.180ms
✓ Accepted
Parsed value:
6
[DEBUG] Total time: 70.284ms