Bayesian A/B testing

bayes_ab is a small package for running Bayesian A/B(/C/D/...) tests.

Installation

bayes_ab can be installed using pip:

pip install bayes_ab

Alternatively, you can clone the repository and use poetry manually:

cd bayes_ab
pip install poetry
poetry install
poetry shell

Tests and metrics

Implemented tests

• BinaryDataTest
  • Input data — binary ([0, 1, 0, ...])
  • Designed for binary data, such as conversions
• PoissonDataTest
  • Input data — integer counts
  • Designed for count data (e.g., number of sales per salesman, deaths per zip code)
• NormalDataTest
  • Input data — normal data with unknown variance
  • Designed for normal data
• DeltaLognormalDataTest
  • Input data — lognormal data with zeros
  • Designed for lognormal data, such as revenue per conversions
• DiscreteDataTest
  • Input data — categorical data with numerical categories
  • Designed for discrete data (e.g. dice rolls, star ratings, 1-10 ratings)

Implemented evaluation metrics

• Chance to beat all
  • Probability of beating all other variants
• Expected Loss
  • Risk associated with choosing a given variant over other variants
  • Measured in the same units as the tested measure (e.g. positive rate or average value)
• Uplift vs. 'A'
  • Relative uplift of a given variant compared to the first variant added
• 95% HDI
  • The central interval containing 95% of the probability. The Bayesian approach allows us to say that, 95% of the time, the 95% HDI will contain the true value

Evaluation metrics are calculated using Monte Carlo simulations from posterior distributions

Decision rules for test continuation

For tests between two variants with binary, Poisson, and normal data, bayes_ab can additionally provide a continuation recommendation—that is, a recommendation as to the variant to select, or to continue testing. See the docstrings and examples for usage guidelines.

The decision method makes use of the following concepts:

• Region of Practical Equivalence (ROPE) — a region [-t, t] of the distribution of differences B - A which is practically equivalent to no uplift. E.g., you may be indifferent between an uplift of +/- 0.1% and no change, in which case the ROPE would be [-0.1, 0.1.
• 95% HDI — the central interval containing 95% of the probability for the distribution of differences B - A.

The recommendation output has three elements:

1. Decision
   • Select either variant if the ROPE is fully contained within the 95% HDI.
   • Select the better variant if the ROPE and the 95% HDI do not overlap.
   • Continue testing if the ROPE partially overlaps the 95% HDI.
   • _Note: There are high-confidence and low-confidence variations of the first two messages.
2. Confidence
   • High if the width of the 95% HDI is less than or equal to 0.8*rope.
   • Low if the width of the 95% HDI is greater than 0.8*rope.
3. Bounds
   • The 95% HDI.

Closed form solutions

For smaller Binary and Poisson samples, metrics calculated from Monte Carlo simulation can be checked against the closed-form solutions by passing closed_form=True to the evaluate() method. Larger samples generate warnings; samples that are larger than a predetermined threshold will raise an error. The larger the sample, however, the closer the simulated value will be to the true value, so closed-form comparisons are recommended to validate metrics for smaller samples only.

Error tolerance

Binary tests with small sample sizes will raise a warning when the error for the expected loss estimate surpasses a set tolerance. To reduce error, increase the simulation count. For more detail, see the docstring for expected_loss_accuracy_bernoulli in evaluation.py

Basic Usage

There are five primary classes:

• BinaryDataTest
• PoissonDataTest
• NormalDataTest
• DeltaLognormalDataTest
• DiscreteDataTest

For each class, there are two methods for inserting data:

• add_variant_data - add raw data for a variant as a list of observations (or numpy 1-D array)
• add_variant_data_agg - add aggregated variant data (this can be practical for a larger data set, as the aggregation can be done outside the package)

Both methods for adding data allow the user to specify a prior distribution (see details in respective docstrings). The default priors are non-informative priors and should be sufficient for most use cases, and in particular when the number of samples or observations is large.

To get the results of the test, simply call method evaluate; to access evaluation metrics as well as the simulated random samples, call the data instance variable.

Chance to beat all and expected loss are approximated using Monte Carlo simulation, so evaluate may return slightly different values for different runs. To decrease variation, you can set the sim_count parameter of evaluate to a higher value (the default is 200K); to fix values, set the seed parameter.

More examples are available in the examples directory, though many examples in this directory are still in the process of being updated to reflect the functionality of the updated package.

BinaryDataTest

Class for Bayesian A/B testing of binary-like data (e.g. conversions, successes, etc.).

Example:

import numpy as np
from bayes_ab.experiments import BinaryDataTest

# generating some random data
rng = np.random.default_rng(52)
# random 1x1500 array of 0/1 data with 5.2% probability for 1:
data_a = rng.binomial(n=1, p=0.052, size=1500)
# random 1x1200 array of 0/1 data with 6.7% probability for 1:
data_b = rng.binomial(n=1, p=0.067, size=1200)

# initialize a test.js:
test = BinaryDataTest()

# add variant using raw data (arrays of zeros and ones) and specifying priors:
test.add_variant_data("A", data_a, a_prior=10, b_prior=17)
test.add_variant_data("B", data_b, a_prior=5, b_prior=30)
# the default priors are a=b=1
# test.js.add_variant_data("C", data_c)

# add variant using aggregated data:
test.add_variant_data_agg("C", total=1000, positives=50)

# evaluate test.js:
test.evaluate(seed=314)

# access simulation samples and evaluation metrics
data = test.data

# generate plots
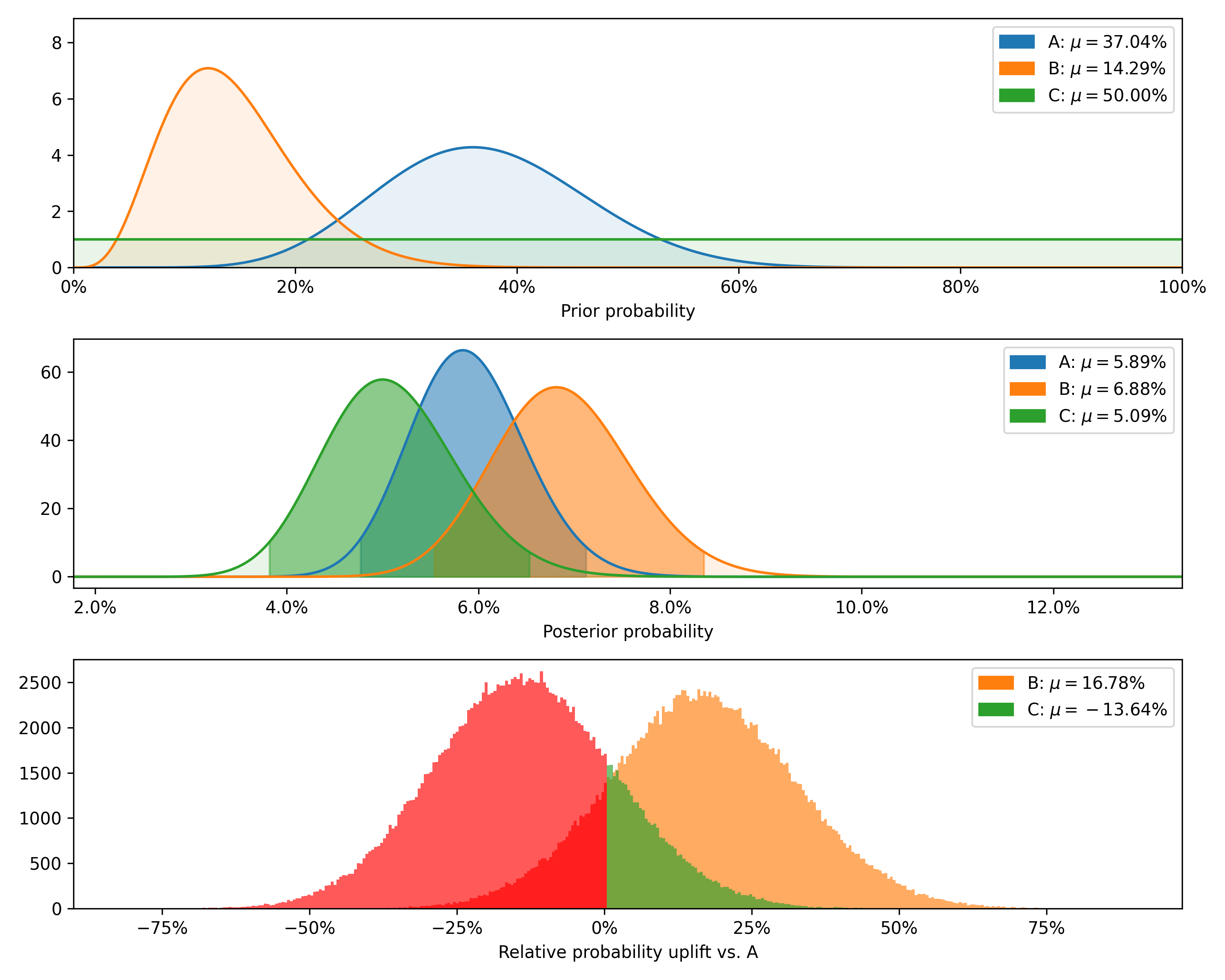
test.plot_distributions(control='A', fname='binary_distributions_example.png')

+---------+--------+-----------+-------------+----------------+--------------------+---------------+----------------+----------------+
| Variant | Totals | Positives | Sample rate | Posterior rate | Chance to beat all | Expected loss | Uplift vs. "A" |    95% HDI     |
+---------+--------+-----------+-------------+----------------+--------------------+---------------+----------------+----------------+
|    B    |  1200  |     80    |    6.67%    |     6.88%      |       83.82%       |     0.08%     |     16.78%     | [5.74%, 8.11%] |
|    C    |  1000  |     50    |    5.00%    |     5.09%      |       2.54%        |     1.87%     |    -13.64%     | [4.00%, 6.28%] |
|    A    |  1500  |     80    |    5.33%    |     5.89%      |       13.64%       |     1.07%     |     0.00%      | [4.94%, 6.92%] |
+---------+--------+-----------+-------------+----------------+--------------------+---------------+----------------+----------------+

For smaller samples, such as the above, it is also possible to check the modeled chance to beat all against the closed-form equivalent by passing closed_form=True.

test.evaluate(closed_form=True, seed=314)

+---------+-------------------------+--------------------------+--------+
| Variant | Est. chance to beat all | Exact chance to beat all | Delta  |
+---------+-------------------------+--------------------------+--------+
|    B    |          83.82%         |          83.58%          | 0.28%  |
|    C    |          2.54%          |          2.56%           | -0.66% |
|    A    |          13.64%         |          13.86%          | -1.59% |
+---------+-------------------------+--------------------------+--------+

Removing variant 'C', as this feature is implemented for two variants only currently, and passing a value to control additionally returns a test-continuation recommendation:

test.delete_variant("C")
test.evaluate(control='A', seed=314)

Decision: Stop and implement either variant. Confidence: Low. Bounds: [-0.84%, 2.85%].

Finally, we can plot the prior and posterior distributions, as well as the distribution of differences.

PoissonDataTest

Class for Bayesian A/B testing of count data. This can be used to compare, e.g., the number of sales per day from different salesmen, or the number of deaths from a given disease per zip code.

Example:

# generating some random data
import numpy as np
from bayes_ab.experiments import PoissonDataTest

# generating some random data
rng = np.random.default_rng(21)
data_a = rng.poisson(43, size=20)
data_b = rng.poisson(39, size=25)
data_c = rng.poisson(37, size=15)

# initialize a test.js:
test = PoissonDataTest()

# add variant using raw data (arrays of zeros and ones) and specifying priors:
test.add_variant_data("A", data_a, a_prior=30, b_prior=7)
test.add_variant_data("B", data_b, a_prior=5, b_prior=5)
# test.js.add_variant_data("C", data_c)

# add variant using aggregated data:
test.add_variant_data_agg("C", total=len(data_c), obs_mean=np.mean(data_c), obs_sum=sum(data_c))

# evaluate test.js:
test.evaluate(seed=314)

# access simulation samples and evaluation metrics
data = test.data

# generate plots
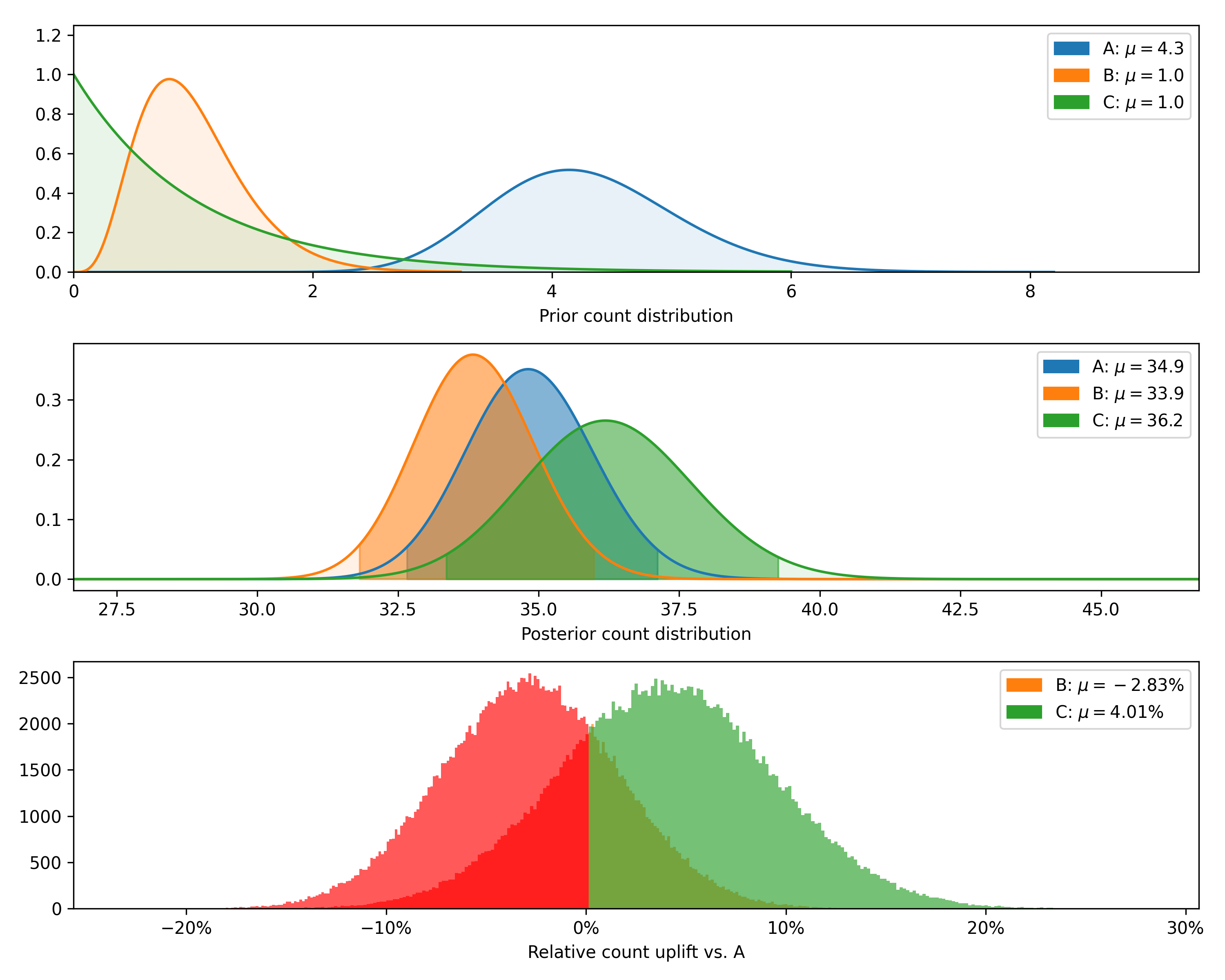
test.plot_distributions(control='A', fname='poisson_distributions_example.png')

+---------+--------------+-------------+----------------+--------------------+---------------+----------------+--------------+
| Variant | Observations | Sample mean | Posterior mean | Chance to beat all | Expected loss | Uplift vs. "A" |   95% HDI    |
+---------+--------------+-------------+----------------+--------------------+---------------+----------------+--------------+
|    C    |      15      |     38.6    |      36.2      |       74.06%       |      0.28     |     4.01%      | [33.8, 38.8] |
|    B    |      25      |     40.4    |      33.9      |       5.09%        |      2.66     |     -2.83%     | [32.1, 35.6] |
|    A    |      20      |     45.6    |      34.9      |       20.85%       |      1.68     |     0.00%      | [33.0, 36.7] |
+---------+--------------+-------------+----------------+--------------------+---------------+----------------+--------------+

For samples smaller than the above, it is also possible to check the modeled chance to beat all against the closed-form equivalent by passing closed_form=True:

test.evaluate(closed_form=True, seed=314)

+---------+-------------------------+--------------------------+--------+
| Variant | Est. chance to beat all | Exact chance to beat all | Delta  |
+---------+-------------------------+--------------------------+--------+
|    C    |          74.06%         |          73.91%          | 0.20%  |
|    B    |          5.09%          |          5.24%           | -2.84% |
|    A    |          20.85%         |          20.85%          | -0.01% |
+---------+-------------------------+--------------------------+--------+

Removing variant 'C', as this feature is implemented for two variants only currently, and passing control and rope additionally returns a test-continuation recommendation:

test.delete_variant("C")
test.evaluate(control='A', rope=0.5, seed=314)

Decision: Stop and implement either variant. Confidence: Low. Bounds: [-4.0, 2.1].

Finally, we can plot the posterior distributions as well as the distribution of differences (returning now to the original number of observations rather than the smaller sample used to show the closed-form validation).

NormalDataTest

Class for Bayesian A/B test for normal data.

Example:

import numpy as np
from bayes_ab.experiments import NormalDataTest

# generating some random data
rng = np.random.default_rng(314)
data_a = rng.normal(6.9, 2, 500)
data_b = rng.normal(6.89, 2, 800)
data_c = rng.normal(7.0, 4, 500)

# initialize a test.js:
test = NormalDataTest()

# add variant using raw data:
test.add_variant_data("A", data_a)
test.add_variant_data("B", data_b, m_prior=5, n_prior=11, v_prior=10, s_2_prior=4)
# test.js.add_variant_data("C", data_c)

# add variant using aggregated data:
test.add_variant_data_agg("C", len(data_c), sum(data_c), sum((data_c - np.mean(data_c)) ** 2), sum(np.square(data_c)))

# evaluate test.js:
test.evaluate(sim_count=200000, seed=314)

# access simulation samples and evaluation metrics
data = test.data

# generate plots
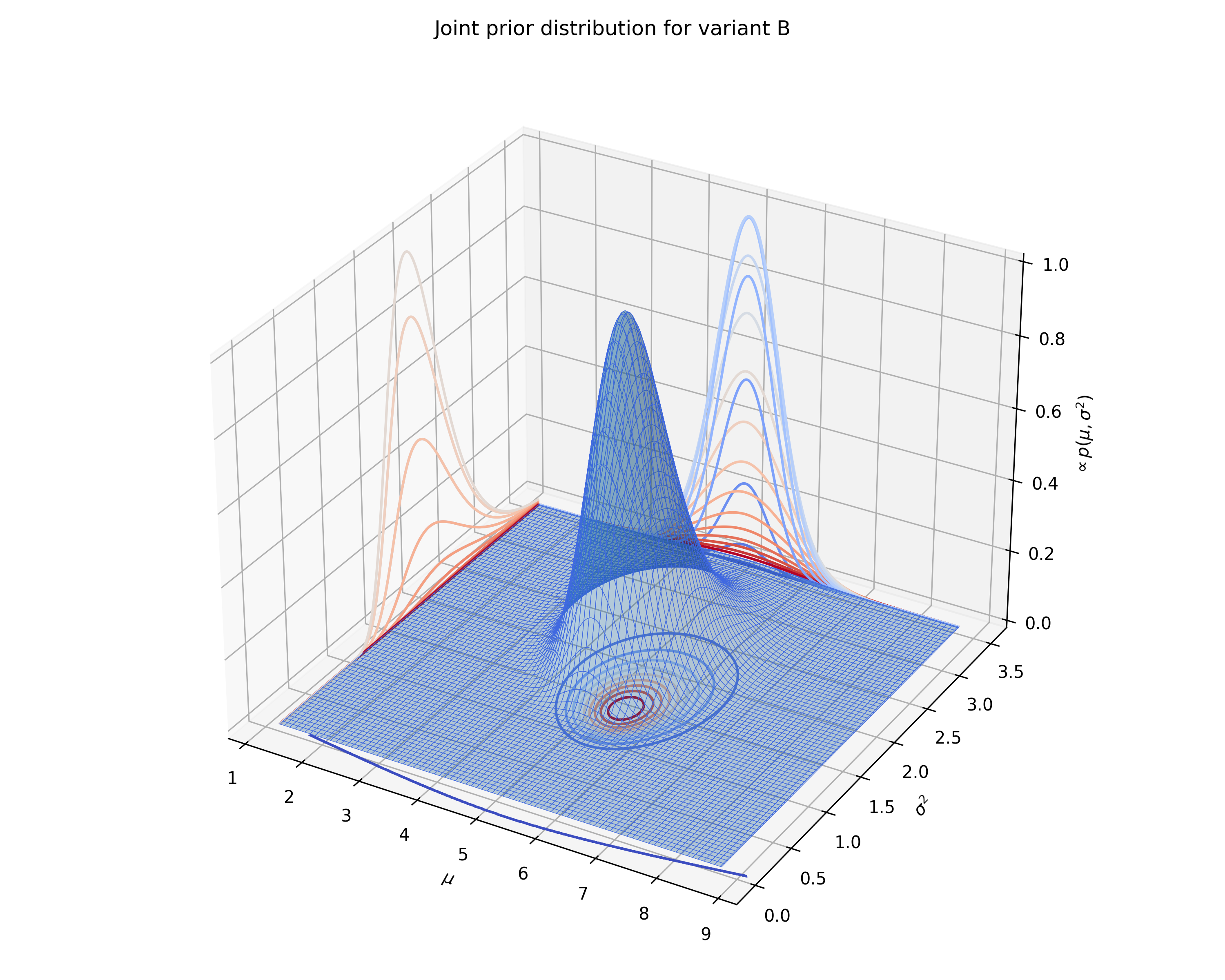
test.plot_joint_prior(variant='B', fname='normal_prior_distribution_B_example.png')
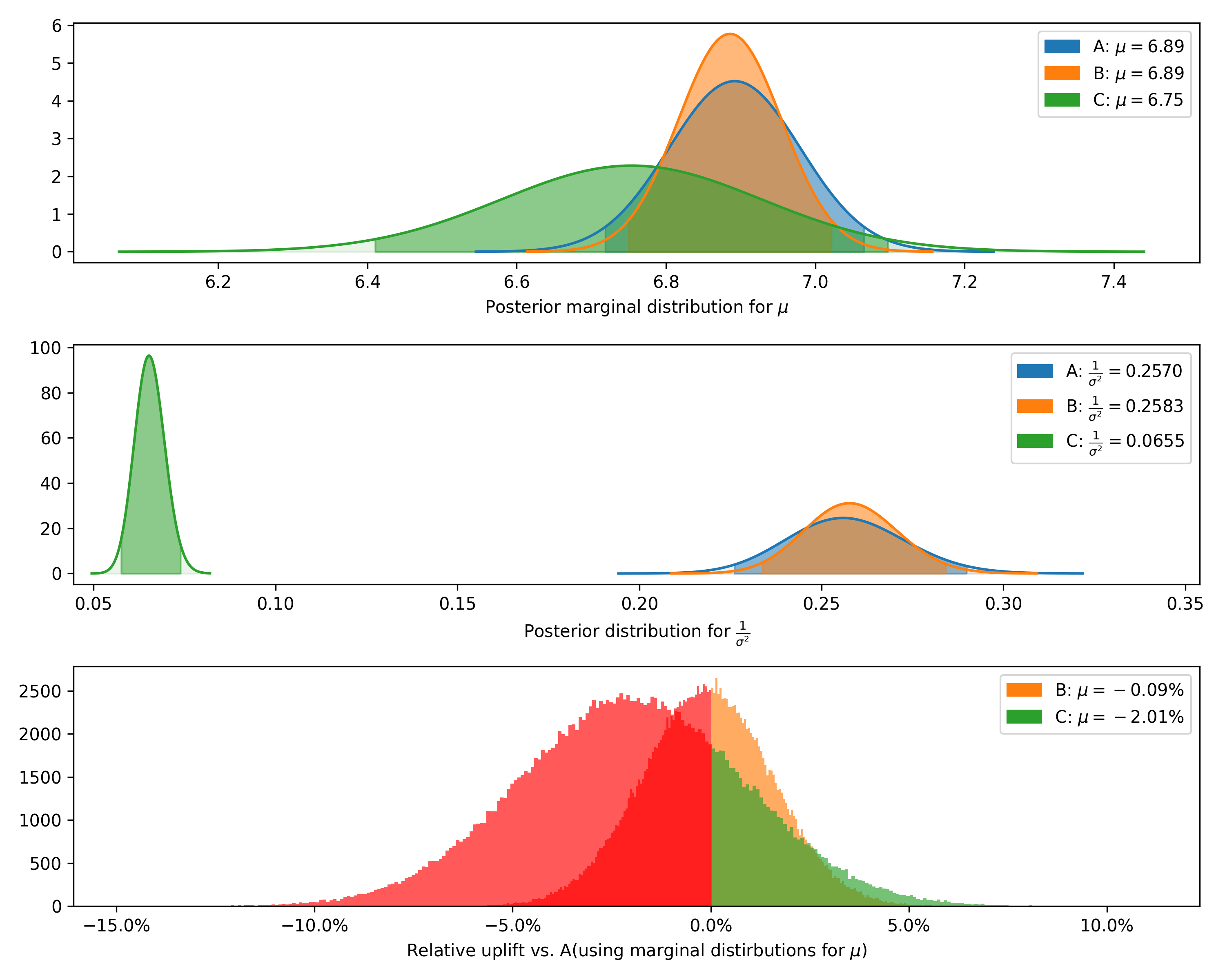
test.plot_distributions(control='A', fname='normal_distributions_example.png')

+---------+--------------+-------------+----------------+-----------+-----------+--------------------+---------------+----------------+----------------+-----------------+
| Variant | Observations | Sample mean | Posterior mean | Precision | Std. dev. | Chance to beat all | Expected loss | Uplift vs. "A" | 95% HDI (mean) | 95% HDI (stdev) |
+---------+--------------+-------------+----------------+-----------+-----------+--------------------+---------------+----------------+----------------+-----------------+
|    A    |     500      |     6.89    |      6.89      |   0.257   |    1.97   |       91.31%       |      0.0      |     0.00%      |  [6.72, 7.07]  |   [1.86, 2.10]  |
|    B    |     800      |     6.91    |      6.89      |   0.258   |    1.97   |       8.69%        |      0.01     |     -0.09%     |  [6.75, 7.02]  |   [1.88, 2.07]  |
|    C    |     500      |     6.75    |      6.75      |   0.065   |    3.91   |       0.00%        |      0.14     |     -2.01%     |  [6.41, 7.10]  |   [3.68, 4.17]  |
+---------+--------------+-------------+----------------+-----------+-----------+--------------------+---------------+----------------+----------------+-----------------+

We can also plot the joint prior distribution for $\mu$ and $\sigma^2$, the posterior distributions for $\mu$ and $\frac{1}{\sigma^2}$, and the distribution of differences from a given control.

DeltaLognormalDataTest

Class for Bayesian A/B testing of delta-lognormal data (log-normal with zeros). Delta-lognormal data is typical case of revenue per session data where many sessions have 0 revenue but non-zero values are positive numbers with possible log-normal distribution. To handle this data, the calculation is combining binary Bayes model for zero vs non-zero "conversions" and log-normal model for non-zero values.

Example:

import numpy as np
from bayes_ab.experiments import DeltaLognormalDataTest

test = DeltaLognormalDataTest()

data_a = [7.1, 0.3, 5.9, 0, 1.3, 0.3, 0, 1.2, 0, 3.6, 0, 1.5, 2.2, 0, 4.9, 0, 0, 1.1, 0, 0, 7.1, 0, 6.9, 0]
data_b = [4.0, 0, 3.3, 19.3, 18.5, 0, 0, 0, 12.9, 0, 0, 0, 10.2, 0, 0, 23.1, 0, 3.7, 0, 0, 11.3, 10.0, 0, 18.3, 12.1]

# adding variant using raw data:
test.add_variant_data("A", data_a)
# test.js.add_variant_data("B", data_b)

# alternatively, variant can be also added using aggregated data:
# (looks more complicated but for large data it can be quite handy to move around only these sums)
test.add_variant_data_agg(
    name="B",
    total=len(data_b),
    positives=sum(x > 0 for x in data_b),
    sum_values=sum(data_b),
    sum_logs=sum([np.log(x) for x in data_b if x > 0]),
    sum_logs_2=sum([np.square(np.log(x)) for x in data_b if x > 0])
)

# evaluate test.js:
test.evaluate(seed=21)

# access simulation samples and evaluation metrics
data = test.data

[{'variant': 'A',
  'totals': 24,
  'positives': 13,
  'sum_values': 43.4,
  'avg_values': 1.80833,
  'avg_positive_values': 3.33846,
  'prob_being_best': 0.04815,
  'expected_loss': 4.0941101},
 {'variant': 'B',
  'totals': 25,
  'positives': 12,
  'sum_values': 146.7,
  'avg_values': 5.868,
  'avg_positive_values': 12.225,
  'prob_being_best': 0.95185,
  'expected_loss': 0.1588627}]

DiscreteDataTest

Class for Bayesian A/B testing for discrete data having a finite number of numerical categories (states). This test can be used, e.g., to find the biases of different dice and to decide which of them of multiple for the "best" of multiple dice) or rating data (e.g. 1-5 stars or 1-10 scale).

Example:

from bayes_ab.experiments import DiscreteDataTest

# dice rolls data for 3 dice - A, B, C
data_a = [2, 5, 1, 4, 6, 2, 2, 6, 3, 2, 6, 3, 4, 6, 3, 1, 6, 3, 5, 6]
data_b = [1, 2, 2, 2, 2, 3, 2, 3, 4, 2]
data_c = [1, 3, 6, 5, 4]

# initialize a test.js with all possible states (i.e. numerical categories):
test = DiscreteDataTest(states=[1, 2, 3, 4, 5, 6])

# add variant using raw data:
test.add_variant_data("A", data_a)
test.add_variant_data("B", data_b)
test.add_variant_data("C", data_c)

# add variant using aggregated data:
# test.js.add_variant_data_agg("C", [1, 0, 1, 1, 1, 1]) # equivalent to rolls in data_c

# evaluate test.js:
test.evaluate(sim_count=200000, seed=52)

# access simulation samples and evaluation metrics
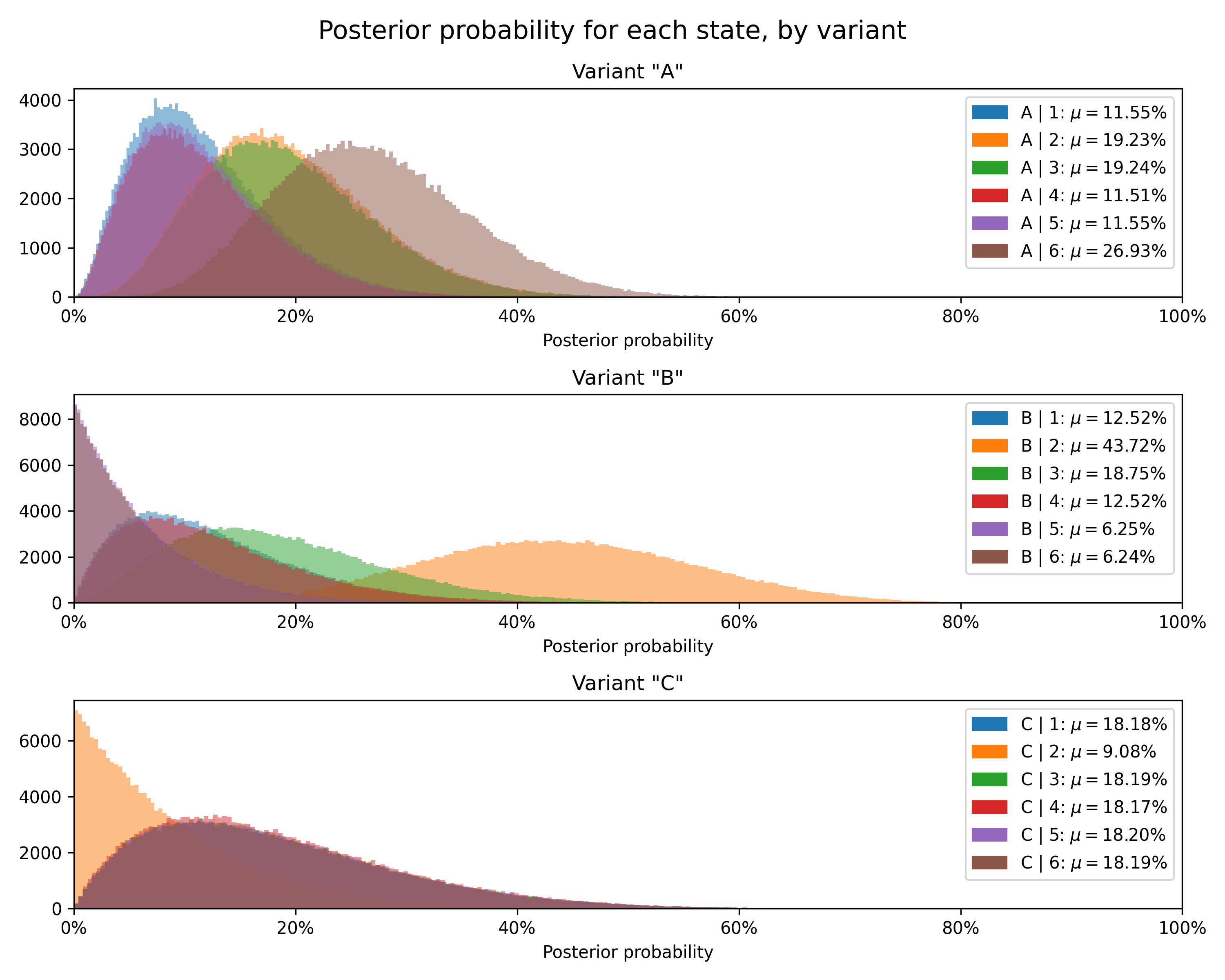
data = test.data

+---------+------------------------------------+-------------+----------------+------------------------------------------------------------------+-------------------------------------------------------------------------------------------------------------------------+--------------------+---------------+----------------+----------------+
| Variant |           Concentrations           | Sample mean | Posterior mean |                          Relative prob.                          |                                                 95% HDI (relative prob.)                                                | Chance to beat all | Expected loss | Uplift vs. "A" | 95% HDI (mean) |
+---------+------------------------------------+-------------+----------------+------------------------------------------------------------------+-------------------------------------------------------------------------------------------------------------------------+--------------------+---------------+----------------+----------------+
|    A    | 1: 2, 2: 4, 3: 4, 4: 2, 5: 2, 6: 6 |     3.8     |      3.73      | 1: 11.54%, 2: 19.23%, 3: 19.23%, 4: 11.54%, 5: 11.54%, 6: 26.92% | 1: [2.55%, 26.02%], 2: [6.82%, 36.06%], 3: [6.85%, 36.12%], 4: [2.54%, 25.96%], 5: [2.59%, 26.09%], 6: [12.10%, 45.17%] |       55.21%       |     19.71%    |     0.00%      |  [3.07, 4.40]  |
|    C    | 1: 1, 2: 0, 3: 1, 4: 1, 5: 1, 6: 1 |     3.8     |      3.64      | 1: 18.18%, 2: 9.09%, 3: 18.18%, 4: 18.18%, 5: 18.18%, 6: 18.18%  |  1: [2.50%, 44.45%], 2: [0.26%, 30.78%], 3: [2.51%, 44.54%], 4: [2.47%, 44.48%], 5: [2.53%, 44.57%], 6: [2.52%, 44.54%] |       44.02%       |     29.09%    |     -2.53%     |  [2.64, 4.58]  |
|    B    | 1: 1, 2: 6, 3: 2, 4: 1, 5: 0, 6: 0 |     2.3     |      2.75      |  1: 12.50%, 2: 43.75%, 3: 18.75%, 4: 12.50%, 5: 6.25%, 6: 6.25%  | 1: [1.66%, 31.97%], 2: [21.33%, 67.67%], 3: [4.31%, 40.47%], 4: [1.65%, 31.96%], 5: [0.17%, 21.78%], 6: [0.17%, 21.84%] |       0.78%        |    117.81%    |    -26.29%     |  [2.18, 3.45]  |
+---------+------------------------------------+-------------+----------------+------------------------------------------------------------------+-------------------------------------------------------------------------------------------------------------------------+--------------------+---------------+----------------+----------------+

Finally, we can plot the posterior distribution for each state for each variant.

Development

To set up a development environment, use Poetry and pre-commit:

pip install poetry
poetry install
poetry run pre-commit install

Roadmap

Improvements in the pipeline:

• Validate and improve DeltaLognormalDataTest
  • Add test continuation assessment (decision, confidence, bounds)
  • Create formatted output
  • Add plotting for posteriors and differences from control
• Update Jupyter examples folder
• Implement sample size/reverse posterior calculation
• Create a method to easily plot evolutions of posteriors and evaluation metrics with time
• Annotate classes with references to the relevant sections within Gelman et al., 2021
• Implement Markov Chain Monte Carlo in place of Monte Carlo, using pymc

References and related work

The development of this package has relied on the resources outlined below. Where a function or method draws directly on a particular derivation, the docstring contains the exact reference.

• Bayesian A/B Testing at VWO (Chris Stucchio, 2015)
• Optional stopping in data collection: p values, Bayes factors, credible intervals, precision (John Kruschke, 2013)
• Is Bayesian A/B Testing Immune to Peeking? Not Exactly (David Robinson, 2015)
• Formulas for Bayesian A/B Testing (Evan Miller, 2015)
• Easy Evaluation of Decision Rules in Bayesian A/B testing (Chris Stucchio, 2014)
• Bayesian Data Analysis, Third Edition (Gelman et al., 2021)
• Bayesian Inference 2019 (Hyvönen & Tolonen, 2019)
• An Introduction to Bayesian Thinking (Clyde et al., 2022)

There is a wealth of material on Bayesian statistics available freely online. A small and somewhat random selection is catalogued below.

• Probabalistic programming and Bayesian methods for hackers ( Cameron Davidson-Pilon, 2022)
• Think Bayes 2 (Downey, 2021)
• Continuous Monitoring of A/B Tests without Pain: Optional Stopping in Bayesian Testing (Deng, Lu, & Chen, 2016)

The dataset tapwater.csv is downloaded from the statsr repository.

This project was inspired by Aubrey Clayton's (2022) Bernoulli's Fallacy: Statistical Illogic and the Crisis of Modern Science.

Select online calculators

• Yanir Seroussi's calculator | project description
• Lyst's calculator | project descrption
• Dynamic Yield's calculator

A note on forking

This package was forked from Matus Baniar's bayesian-testing. Upon deciding to take package development in a different direction, I detached the fork from the original repository. The original author's contributions are large, however, with his central contributions being to the development of the core infrastructure of the project. This being the first package I have worked on, the original author's work to prepare this code for packaging has also been instrumental to package publication, not to mention educative.