Matrix库的诞生让矩阵操作在C中也可以玩的很溜!
[toc]
Matrix库中,矩阵的存储结构采用的是链表和数组结合的形式,矩阵的每一行串成一个链表,而每一行的数据则采用的数组进行存储,最终的结果是平均了链表和数组的优缺点。Matrix库中采用的是二维double类型的矩阵(未来可能会根据需求拓展到高维矩阵上去),支持矩阵的加减、乘、转置、换行、数乘、累加、求逆、求行列式、解线性方程组等基本操作,总之,这个库我认为很棒!
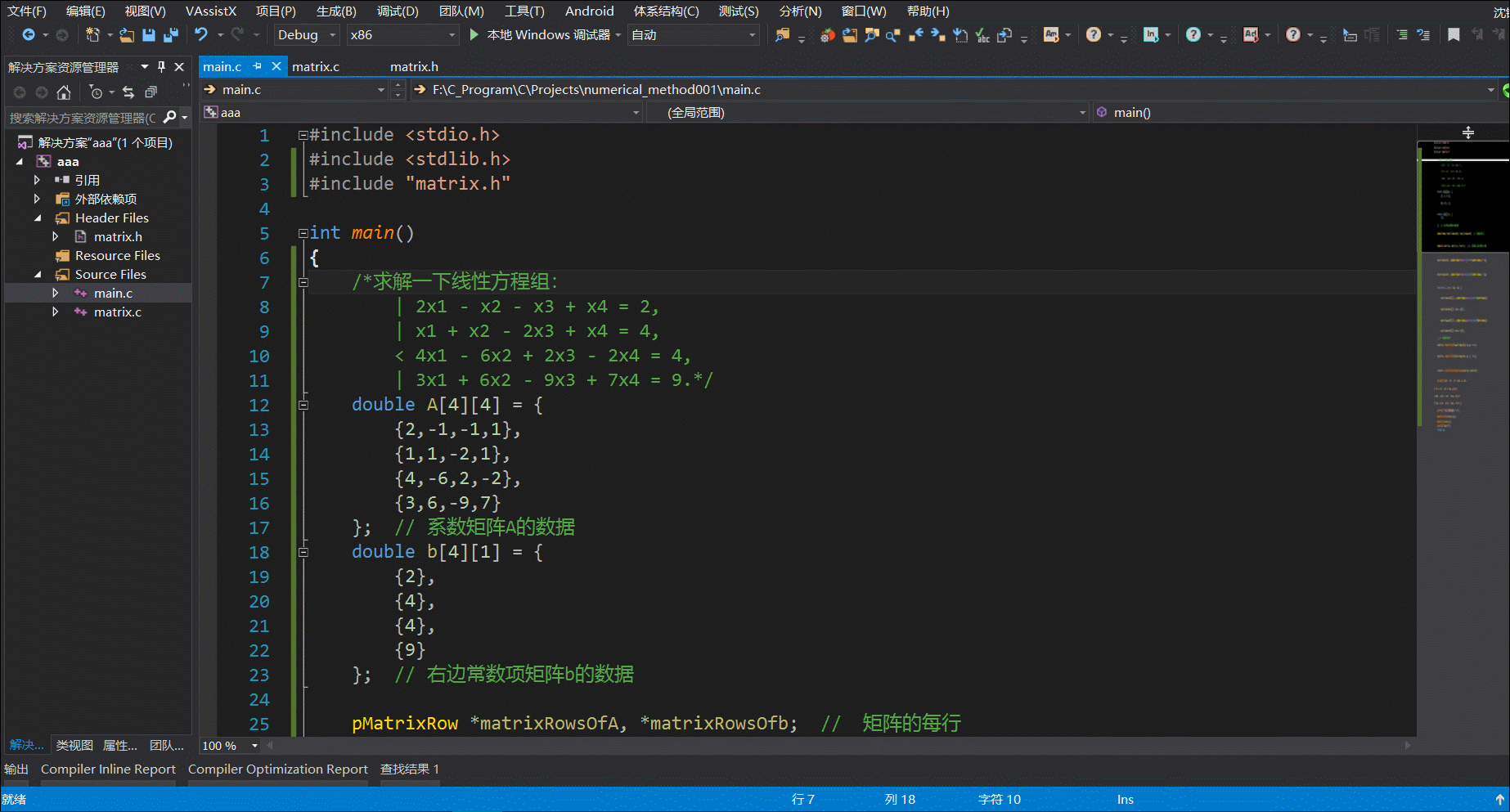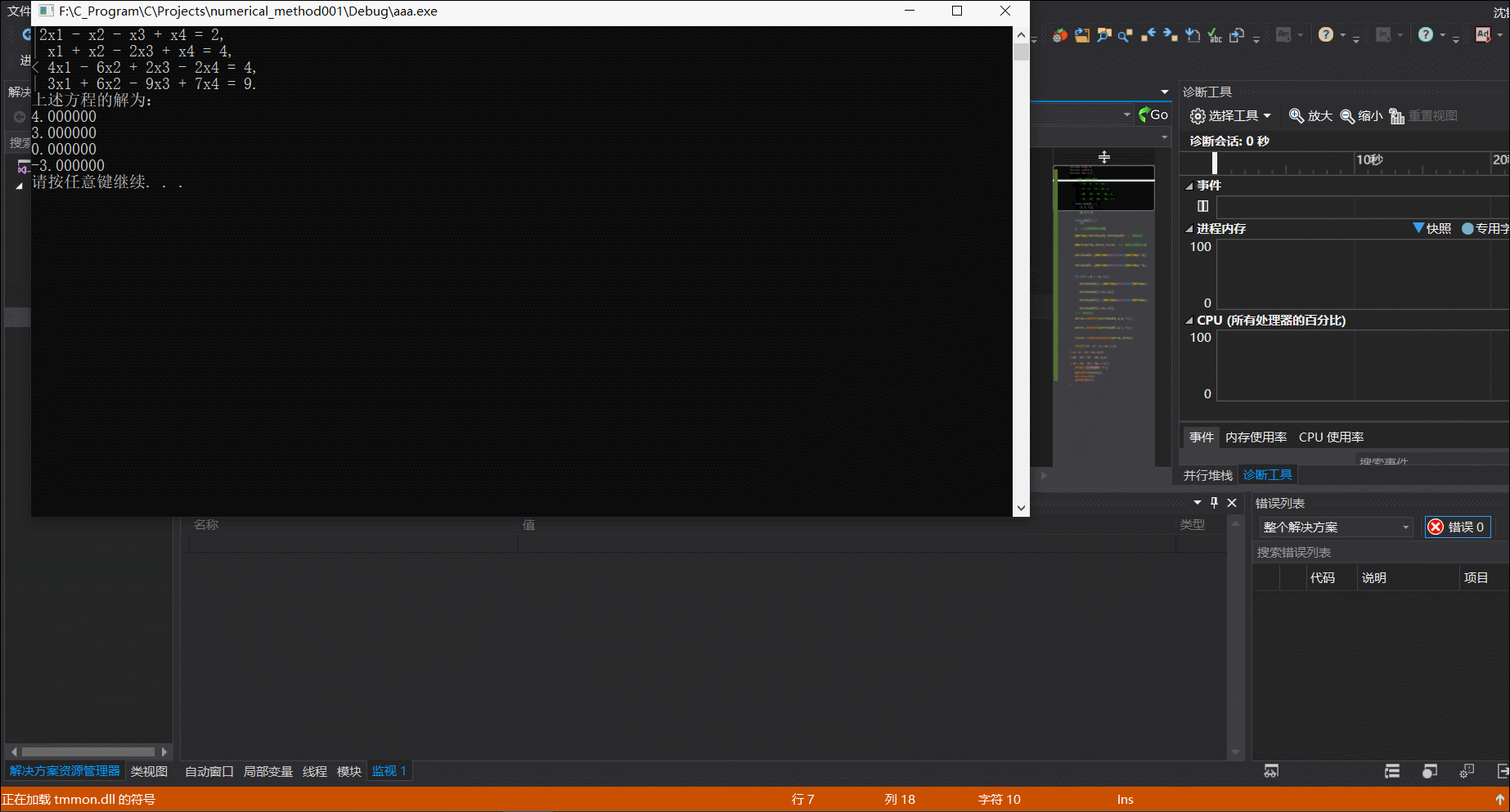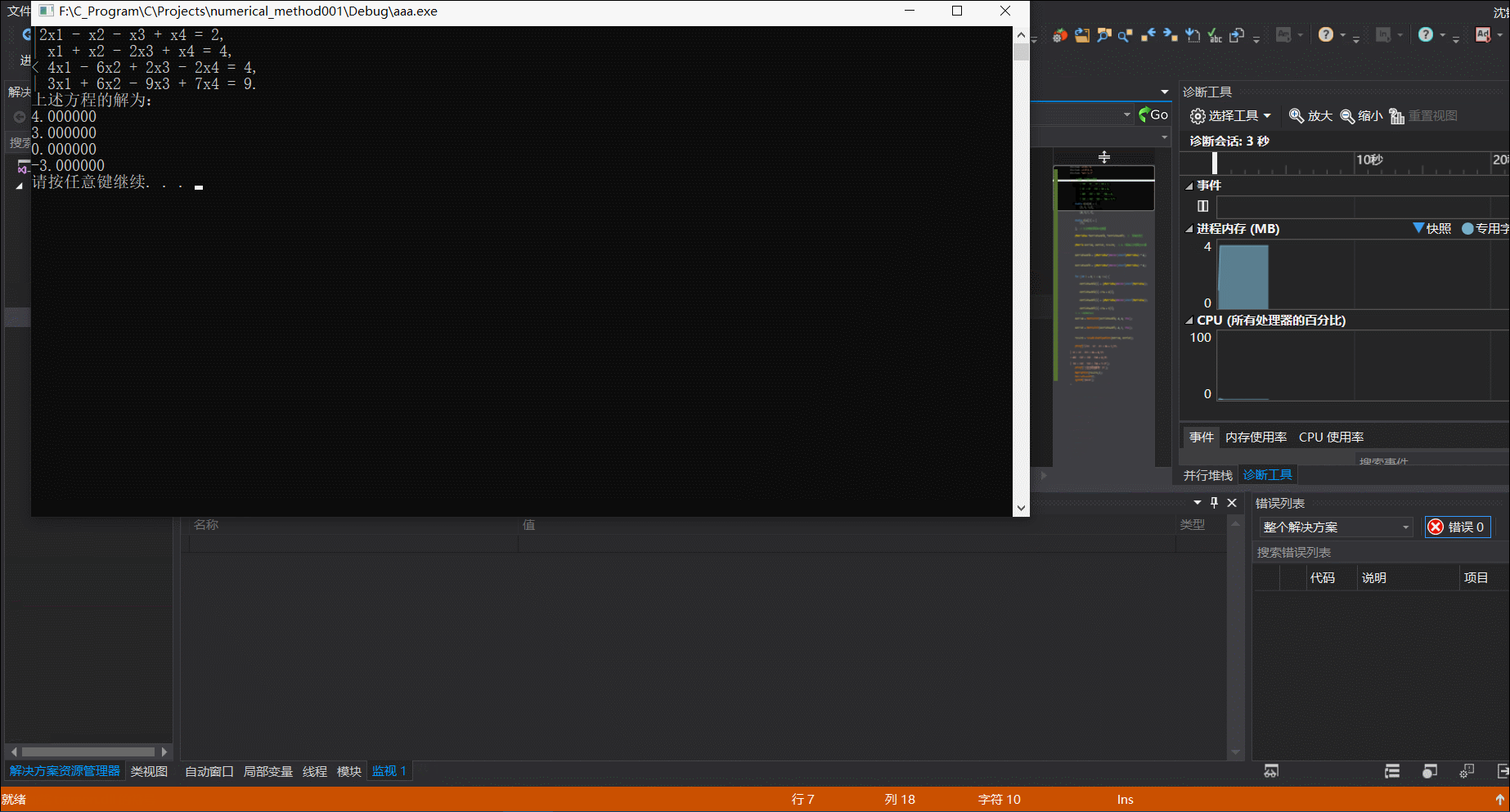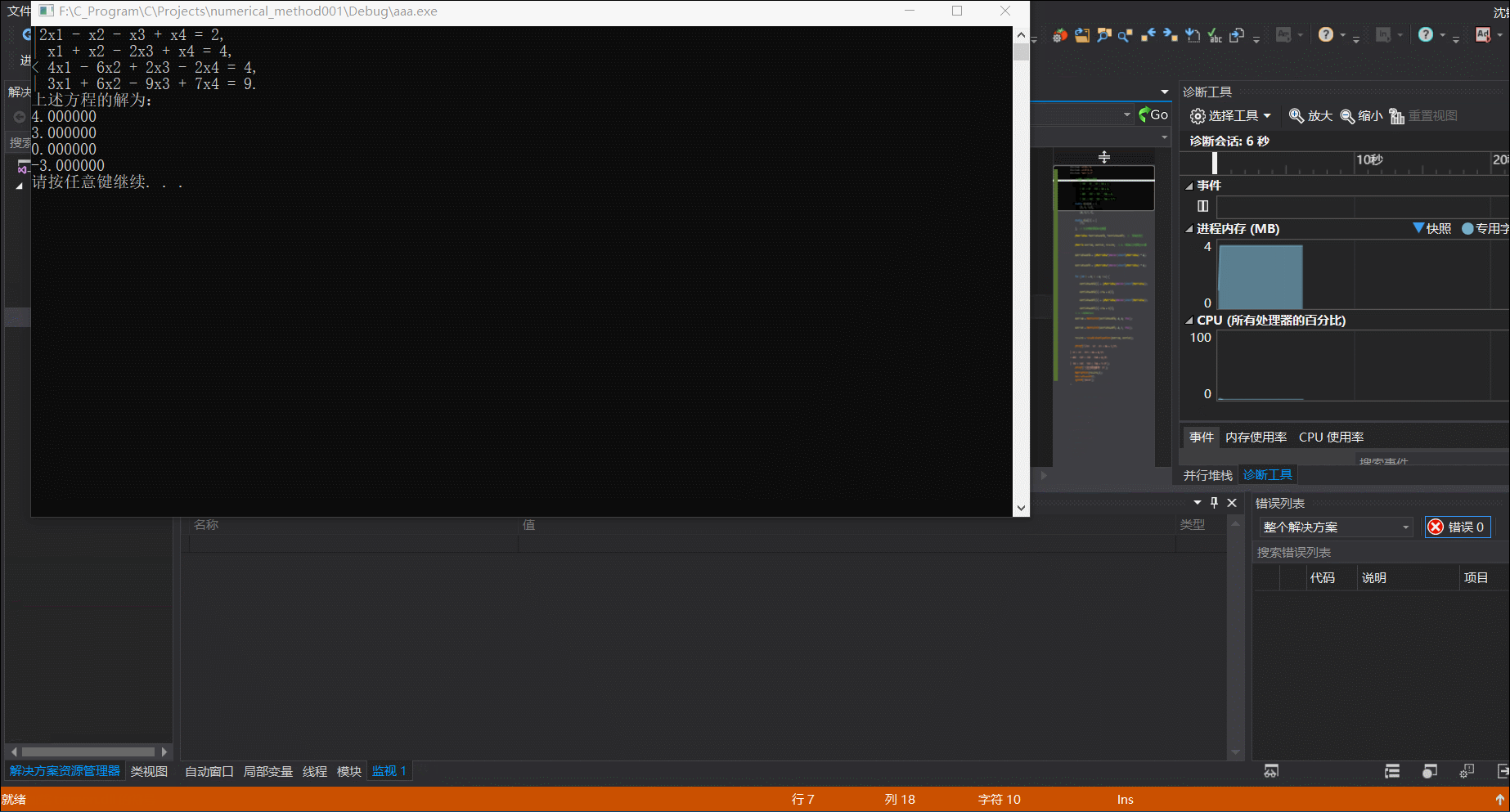
这里将给一段使用Matrix库求解一组线性方程的例子:
#include <stdio.h>
#include <stdlib.h>
#include "matrix.h"
int main()
{
/*求解一下线性方程组:
| 2x1 - x2 - x3 + x4 = 2,
| x1 + x2 - 2x3 + x4 = 4,
< 4x1 - 6x2 + 2x3 - 2x4 = 4,
| 3x1 + 6x2 - 9x3 + 7x4 = 9.*/
double A[4][4] = {
{2,-1,-1,1},
{1,1,-2,1},
{4,-6,2,-2},
{3,6,-9,7}
}; // 系数矩阵A的数据
double b[4][1] = {
{2},
{4},
{4},
{9}
}; // 右边常数项矩阵b的数据
pMatrixRow *matrixRowsOfA, *matrixRowsOfb; // 矩阵的每行
pMatrix matrixA, matrixb, resultx; // A、b矩阵以及结果的x向量
matrixRowsOfA = (pMatrixRow*)malloc(sizeof(pMatrixRow) * 4);
matrixRowsOfb = (pMatrixRow*)malloc(sizeof(pMatrixRow) * 4);
// 矩阵每行初始化
for (int i = 0; i < 4; i++) {
matrixRowsOfA[i] = (pMatrixRow)malloc(sizeof(MatrixRow));
matrixRowsOfA[i]->row = A[i];
matrixRowsOfb[i] = (pMatrixRow)malloc(sizeof(MatrixRow));
matrixRowsOfb[i]->row = b[i];
}
// A,b矩阵初始化
matrixA = MatrixInit(matrixRowsOfA, 4, 4, true);
matrixb = MatrixInit(matrixRowsOfb, 4, 1, true);
// 线性方程组求解
resultx = SolveLinearEquations(matrixA, matrixb);
printf("|2x1 - x2 - x3 + x4 = 2,\n\
| x1 + x2 - 2x3 + x4 = 4,\n\
< 4x1 - 6x2 + 2x3 - 2x4 = 4,\n\
| 3x1 + 6x2 - 9x3 + 7x4 = 9.\n");
printf("上述方程的解为:\n");
// 打印矩阵
MatrixPrint(resultx,6);
// 清理矩阵
MatrixCleanAll();
system("pause");
return 0;
}上面简短的代码中我们便成功求解了一个线性方程组,这里我们只需搞清楚MatrixRow和Matrix的区别(pMatrixRow和pMatrix是MatrixRow和Matrix的指针形态),前者是指矩阵的一行,后者代表整个矩阵,矩阵的初始化就是把矩阵每一行的MatrixRow传入MatrixInit函数中,其便会返回初始化后的矩阵。
你可能对上面的MatrixCleanAll函数产生好奇,是的,这个库中实现了自动清理机制,调用该函数便会清理所有矩阵,大大降低了内存溢出的可能性。其还有个兄弟函数——MatrixClean,这个函数尽会清理重要级别为false的矩阵,这也就意味着,我们可以使用随用随销的矩阵,而不必为给每个矩阵变量起名字而苦恼。
上述程序的运行动图如下: