Liczby naturalne Churcha

Abstrakcyjny system liczb naturalnych

Zbiór liczb naturalnych

Przyzwyczailiśmy się, że liczby naturalne to po prostu nieskończony zbiór liczb, poczynając od zera (lub, jak kto woli, od jedynki): 0, 1, 2, 3… itd. Możemy to zapisać jako N= { 0, 1, 3…}. Co jeśli chcielibyśmy to uogólnić? Zbiór ten spełnia następujące warunki:

• Każdy element posiada swojego następnika
• Każdy, poza elementem zerowym, ma swojego poprzednika, którego jest następnikiem

Na pomysł uogólnionego zapis zbioru naturalnego wpadł matematyk i logik - Alonzo Church. Stwierdził on, że każdy zbiór spełniający powyższe zasady można zbudować używając jedynie rachunku lambda, bez używania żadnych liczb, tworząc tym samym najbardziej abstrakcyjny zbiór naturalny.

Możemy bowiem operować zarówno na liczbach: 0, 1, 2, 3… jak i na procesie budowy wieży z klocków: zero to brak wieży, jego następnik to klocek, którego następnikiem jest wieża powiększona o kolejny klocek, itd.

Liczby naturalne Churcha

Do zilustrowania procesu budowania liczb naturalnych Churcha użyję opisu słownego i zapisu matematycznego:

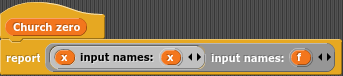
• 0 - funkcja za argument biorąca f i zwracająca funkcję tożsamościową (funkcja która zwraca swój argument, nie zmieniając go w żaden sposób), a więc: λf.λx.x.

• 1 - funkcja, która bierze funkcję i zwraca funkcję od x wykonującą f na x, zapis matematyczny to λf.λx.f(x).

• 2 - funkcja, która bierze funkcję i zwraca funkcję od x wykonującą f na f od x, zapis matematyczny to λf.λx.f(f(x)).

Można zauważyć tu pewną zależność, każdy następnik to po prostu kolejne złożenie funkcji:

• λf.λx.x
• λf.λx.f(x)
• λf.λx.f( f(x) )
• λf.λx.f( f( f(x) ) )
• ...
• λf.λx.fn(x)

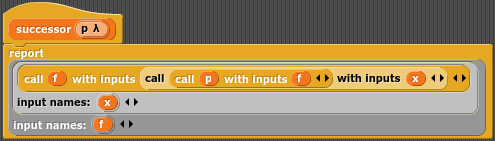
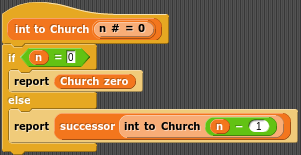
Odetchnijmy trochę od tego matematycznego zapisu i przejdźmy do programowania, zaimplementujmy teraz church zero, następnika i zmianę inta na liczebnik churcha. Przykłady implementacji prezentować będę w języku javascript (w dwóch wersjach) i Snap.

JS:

function church_zero( f ) {
  return function( x ) {
    return x;
  };
};

function successor( p ) {
  return function( f ) {
    return function( x ) {
      return f(p(f)(x));
    };
  };
};

function int_to_church( x ) {
    if( x == 0 ) return church_zero;
    else         return successor( int_to_church( x-1 ) );
}

function church_to_int( f ) {
    return f( function(x){ return x+1; ) )( 0 );
}

Możemy uprościć też zapis używając fat arrow notation:

var church_zero = f => ( x => x );

var successor = p => f => x => f(p(f)(x));

var int_to_church = x => {
    if( x == 0 ) return church_zero;
    else         return successor( church( x-1 ) );
};

var church_to_int = f => f(x=>x+1)(0);

Snap:

Warto przyjrzeć się church_to_int - aby z liczby naturalnej Churcha otrzymać liczbę całkowitą należy wywołać ją z funkcją inkrementacji, co zwróci nam odpowiednią ilość złożeń dodawania jeden do argumentu i wywołać to z zerem.

Operacje na liczbach naturalnych Churcha

Wiemy już jak tworzyć liczby naturalne Churcha. Byłyby one jednak bez znaczenia gdybyśmy nie mogli wykonywać na nich operacji arytmetycznych, tak jak na zbiorze liczb naturalnych:

a, b - liczby naturalne Churcha

• a + b = λca.λb.λf.λx.a(f)(b(f)(x))
• a * b = λa.λb.λf.a(b(f))
• a ^ b = λa.λb.a(b)

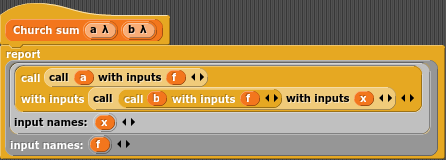
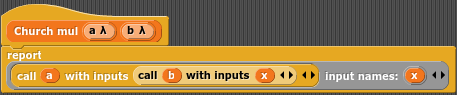
Zdecydowanie łatwiej jest zrozumieć to zaimplementowane w kodzie, ponownie w Javascript (tym razem w jednej, czytelniejszej wersji) i Snapie:

JS:

var churchplus = function(a,b) {
  return function(f) {
    return function(x) {
      return a(f)(b(f)(x));
    };
  };
}

var churchmul = function( a, b ) {
    return function(x) {
      return a( b (x));
    };
};

var churchexp = function( a, b ) {
    return function( x ) {
        return (b(a))(x);
    } 
}

Snap:

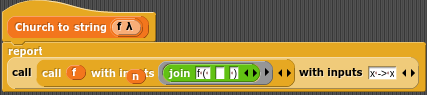
Możemy jeszcze pokusić się o zaimplementowanie funkcji zmieniającej liczbę naturalną Churcha na string obrazujący ilość złożeń funkcji f.

JS:

function church_to_string( f ) {
	return f( x=> "f(" + x + ")" )( "x -> x" );
}

Snap:

Skoro mamy już zaimplementowany zbiór liczb naturalnych Churcha to warto pokazać, że nie musimy operować wyłącznie na liczbach. Pomyślmy o pozycji sprite’a ze Snapa jako o systemie liczb naturalnych. Pozycja startowa to nasze 0, jej następnikiem jest przesunięcie się o krok itd. Każda pozycja ma swojego następnika jako pozycję o krok dalej.

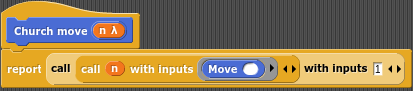
Do implementacji kroku w przód możemy użyć funkcji która bierze długość kroku i porusza spritem o podaną długość, po czym ją zwraca:

Do poruszania spritem liczebnikami Churcha należy tylko lekko zmodyfikować church_to_string lub church_to_int:

Po wywołaniu:

Nasz sprite przesunie się o 100 kroków naprzód. Warto zwrócić uwagę, że do funkcji nie przekazujemy liczby, a (w uproszczeniu) funkcję złożoną 100 razy.

Abstrakcyjność liczb naturalnych Churcha

Zaimplementowaliśmy system liczb naturalnych Churcha i pokazaliśmy jego zastosowania, rozpoczynając od zamiany na liczbę, poprzez zamianę na string, kończąc na abstrakcyjnej zamianie na pozycję sprite’a na ekranie, udowadniając tym samym, że jest to najbardziej ogólny zbiór liczb naturalnych jaki możemy sobie wymyślić.

---

Kod źródłowy (plik XML, który można zaimportować) dostępny jest do pobrania tutaj.