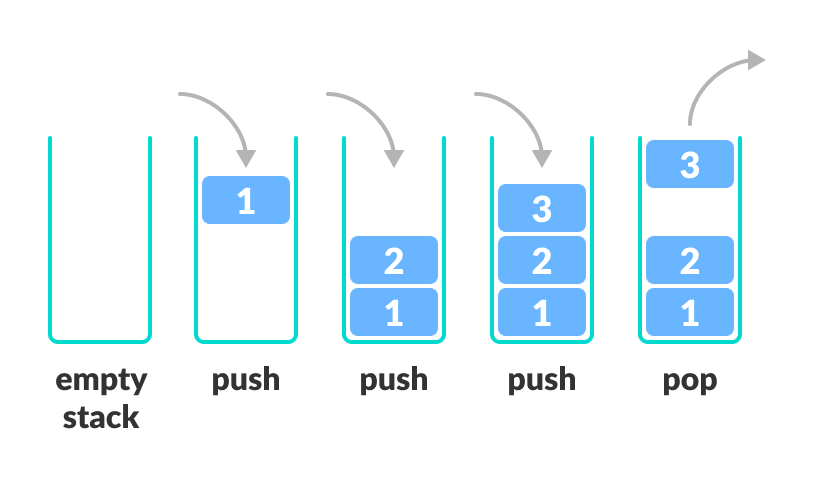
Stack is a linear data structure which follows a particular order in which the operations are performed. The order may be LIFO(Last In First Out) or FILO(First In Last Out). If we make an analogy with real life, Stack is similar to plates stacked over one another in the kitchen. The plate which is at the top is the first one to be removed, the plate which has been placed at the bottommost position remains in the stack for the longest period of time.
| Operations | Time Complexity |
|---|---|
| push() | O(1) |
| pop() | O(1) |
| isEmpty() | O(1) |
| peek() | O(1) |
- push() : Adds an item in the stack. If the stack is full, then it is said to be an Overflow condition.
- pop() : Removes an item from the stack. The items are popped in the reversed order in which they are pushed. If the stack is empty, then it is said to be an Underflow condition.
- peek() : Returns top element of stack.
- isEmpty() : Returns true if stack is empty, else false.
Time Complexities of operations on stack:
push(), pop(), isEmpty() and peek() all take O(1) time. We do not run any loop in any of these operations.
- Balancing of symbols
- Infix to Postfix/Prefix conversion
- Redo-undo features at many places like editors, photoshop
- Forward and backward feature in web browsers
- Used in many algorithms like Tower of Hanoi, tree traversals, stock span problem, histogram problem.
- Stack data structure used in backtracking problems.
There are two ways to implement a stack:
- Using array
- Using linked list
Java language
/* Java program to implement basic stack
operations */
class Stack {
static final int MAX = 1000;
int top;
int a[] = new int[MAX]; // Maximum size of Stack
boolean isEmpty()
{
return (top < 0);
}
Stack()
{
top = -1;
}
boolean push(int x)
{
if (top >= (MAX - 1)) {
System.out.println("Stack Overflow");
return false;
}
else {
a[++top] = x;
System.out.println(x + " pushed into stack");
return true;
}
}
int pop()
{
if (top < 0) {
System.out.println("Stack Underflow");
return 0;
}
else {
int x = a[top--];
return x;
}
}
int peek()
{
if (top < 0) {
System.out.println("Stack Underflow");
return 0;
}
else {
int x = a[top];
return x;
}
}
}
// Driver code
class Main {
public static void main(String args[])
{
Stack s = new Stack();
s.push(10);
s.push(20);
s.push(30);
System.out.println(s.pop() + " Popped from stack");
}
}Output:
10 pushed into stack
20 pushed into stack
30 pushed into stack
30 Popped from stack
Top element is : 20
Elements present in stack : 20 10
Pros: Easy to implement. Memory is saved as pointers are not involved.
Cons: It is not dynamic. It doesn’t grow and shrink depending on needs at runtime.
Java language
// Java Code for Linked List Implementation
public class StackAsLinkedList {
StackNode root;
static class StackNode {
int data;
StackNode next;
StackNode(int data) { this.data = data; }
}
public boolean isEmpty()
{
if (root == null) {
return true;
}
else
return false;
}
public void push(int data)
{
StackNode newNode = new StackNode(data);
if (root == null) {
root = newNode;
}
else {
StackNode temp = root;
root = newNode;
newNode.next = temp;
}
System.out.println(data + " pushed to stack");
}
public int pop()
{
int popped = Integer.MIN_VALUE;
if (root == null) {
System.out.println("Stack is Empty");
}
else {
popped = root.data;
root = root.next;
}
return popped;
}
public int peek()
{
if (root == null) {
System.out.println("Stack is empty");
return Integer.MIN_VALUE;
}
else {
return root.data;
}
}
// Driver code
public static void main(String[] args)
{
StackAsLinkedList sll = new StackAsLinkedList();
sll.push(10);
sll.push(20);
sll.push(30);
System.out.println(sll.pop()
+ " popped from stack");
System.out.println("Top element is " + sll.peek());
}
}Output:
10 pushed to stack
20 pushed to stack
30 pushed to stack
30 popped from stack
Top element is 20
Elements present in stack : 20 10
Pros: The linked list implementation of stack can grow and shrink according to the needs at runtime.
Cons: Requires extra memory due to involvement of pointers.
Queue is a linear data structure which follows a particular order in which the operations are performed. The order is First In First Out (FIFO). A good example of queue is any queue of consumers for a resource where the consumer that came first is served first.
Queue operations work as follows:
- two pointers FRONT and REAR
- FRONT track the first element of the queue
- REAR track the last element of the queue
- initially, set value of FRONT and REAR to -1
- enqueue(): Add an element to the end of the queue
- dequeue(): Remove an element from the front of the queue
- isEmpty(): Check if the queue is empty
- isFull(): Check if the queue is full
- peek(): Get the value of the front of the queue without removing it
| Operations | Time Complexity |
|---|---|
| enqueue() | O(1) |
| dequeue() | O(1) |
| isEmpty() | O(1) |
| peek() | O(1) |
Queue is used when things don’t have to be processed immediatly, but have to be processed in First InFirst Out order.
- CPU scheduling, Disk Scheduling
- When data is transferred asynchronously between two processes.The queue is used for synchronization. For example: IO Buffers, pipes, file IO, etc
- Handling of interrupts in real-time systems.
- Call Center phone systems use Queues to hold people calling them in order.
Java language
// A class to represent a queue
class Queue {
int front, rear, size;
int capacity;
int array[];
public Queue(int capacity)
{
this.capacity = capacity;
front = this.size = 0;
rear = capacity - 1;
array = new int[this.capacity];
}
// Queue is full when size becomes
// equal to the capacity
boolean isFull(Queue queue)
{
return (queue.size == queue.capacity);
}
// Queue is empty when size is 0
boolean isEmpty(Queue queue)
{
return (queue.size == 0);
}
// Method to add an item to the queue.
// It changes rear and size
void enqueue(int item)
{
if (isFull(this))
return;
this.rear = (this.rear + 1)
% this.capacity;
this.array[this.rear] = item;
this.size = this.size + 1;
System.out.println(item
+ " enqueued to queue");
}
// Method to remove an item from queue.
// It changes front and size
int dequeue()
{
if (isEmpty(this))
return Integer.MIN_VALUE;
int item = this.array[this.front];
this.front = (this.front + 1)
% this.capacity;
this.size = this.size - 1;
return item;
}
// Method to get front of queue
int front()
{
if (isEmpty(this))
return Integer.MIN_VALUE;
return this.array[this.front];
}
// Method to get rear of queue
int rear()
{
if (isEmpty(this))
return Integer.MIN_VALUE;
return this.array[this.rear];
}
}
// Driver class
public class Test {
public static void main(String[] args)
{
Queue queue = new Queue(1000);
queue.enqueue(10);
queue.enqueue(20);
queue.enqueue(30);
queue.enqueue(40);
System.out.println(queue.dequeue()
+ " dequeued from queue\n");
System.out.println("Front item is "
+ queue.front());
System.out.println("Rear item is "
+ queue.rear());
}
} Output:
10 enqueued to queue
20 enqueued to queue
30 enqueued to queue
40 enqueued to queue
10 dequeued from queue
Front item is 20
Rear item is 40
Pros of Array Implementation:
- Easy to implement.
Cons of Array Implementation:
- Static Data Structure, fixed size.
- If the queue has a large number of enqueue and dequeue operations, at some point we may not we able to insert elements in the queue even if the queue is empty (this problem is avoided by using circular queue).
Java language
class QNode {
int key;
QNode next;
// constructor to create a new linked list node
public QNode(int key)
{
this.key = key;
this.next = null;
}
}
// A class to represent a queue
// The queue, front stores the front node of LL and rear stores the
// last node of LL
class Queue {
QNode front, rear;
public Queue()
{
this.front = this.rear = null;
}
// Method to add an key to the queue.
void enqueue(int key)
{
// Create a new LL node
QNode temp = new QNode(key);
// If queue is empty, then new node is front and rear both
if (this.rear == null) {
this.front = this.rear = temp;
return;
}
// Add the new node at the end of queue and change rear
this.rear.next = temp;
this.rear = temp;
}
// Method to remove an key from queue.
void dequeue()
{
// If queue is empty, return NULL.
if (this.front == null)
return;
// Store previous front and move front one node ahead
QNode temp = this.front;
this.front = this.front.next;
// If front becomes NULL, then change rear also as NULL
if (this.front == null)
this.rear = null;
}
}
// Driver class
public class Test {
public static void main(String[] args)
{
Queue q = new Queue();
q.enqueue(10);
q.enqueue(20);
q.dequeue();
q.dequeue();
q.enqueue(30);
q.enqueue(40);
q.enqueue(50);
q.dequeue();
System.out.println("Queue Front : " + q.front.key);
System.out.println("Queue Rear : " + q.rear.key);
}
}Output:
Queue Front : 40
Queue Rear : 50
A linked list data structure includes a series of connected nodes. Each node store the data and the address of the next node.

- traverse(): To traverse all the nodes one after another.
- insert(): To add a node at the given position.
- delete(): To delete a node.
- search(): To search an element(s) by value.
- update(): To update a node.
|Operation| Time Complexity| |--|--|--| | traverse()| O(n) | | insert()| O(1)| | delete()| O(1)| | search()| O(n)|
- Singly Linked List.
- Doubly Linked List.
- Circular Linked List.
A Singly-linked list is a collection of nodes linked together in a sequential way where each node of the singly linked list contains a data field and an address field that contains the reference of the next node.
A Doubly Linked List contains an extra memory to store the address of the previous node, together with the address of the next node and data which are there in the singly linked list. So, here we are storing the address of the next as well as the previous nodes.
The nodes are connected to each other in this form where the first node has prev = NULL and the last node has next = NULL.
A circular linked list is either a singly or doubly linked list in which there are no NULL values. Here, we can implement the Circular Linked List by making the use of Singly or Doubly Linked List. In the case of a singly linked list, the next of the last node contains the address of the first node and in case of a doubly-linked list, the next of last node contains the address of the first node and prev of the first node contains the address of the last node.
Applications of linked list in computer science –
- Implementation of stacks and queues
- Implementation of graphs : Adjacency list representation of graphs is most popular which is uses linked list to store adjacent vertices.
- Dynamic memory allocation : We use linked list of free blocks.
- Maintaining directory of names
Applications of linked list in real world-
- Image viewer – Previous and next images are linked, hence can be accessed by next and previous button.
- Previous and next page in web browser – We can access previous and next url searched in web browser by pressing back and next button since, they are linked as linked list.
- Music Player – Songs in music player are linked to previous and next song. you can play songs either from starting or ending of the list.
Java language
import java.io.*;
// Java program to implement
// a Singly Linked List
public class LinkedList {
Node head; // head of list
// Linked list Node.
// This inner class is made static
// so that main() can access it
static class Node {
int data;
Node next;
// Constructor
Node(int d)
{
data = d;
next = null;
}
}
// Method to insert a new node
public static LinkedList insert(LinkedList list, int data)
{
// Create a new node with given data
Node new_node = new Node(data);
new_node.next = null;
// If the Linked List is empty,
// then make the new node as head
if (list.head == null) {
list.head = new_node;
}
else {
// Else traverse till the last node
// and insert the new_node there
Node last = list.head;
while (last.next != null) {
last = last.next;
}
// Insert the new_node at last node
last.next = new_node;
}
// Return the list by head
return list;
}
// Method to print the LinkedList.
public static void printList(LinkedList list)
{
Node currNode = list.head;
System.out.print("LinkedList: ");
// Traverse through the LinkedList
while (currNode != null) {
// Print the data at current node
System.out.print(currNode.data + " ");
// Go to next node
currNode = currNode.next;
}
}
// Driver code
public static void main(String[] args)
{
/* Start with the empty list. */
LinkedList list = new LinkedList();
//
// ******INSERTION******
//
// Insert the values
list = insert(list, 1);
list = insert(list, 2);
list = insert(list, 3);
list = insert(list, 4);
list = insert(list, 5);
list = insert(list, 6);
list = insert(list, 7);
list = insert(list, 8);
// Print the LinkedList
printList(list);
}
}Trees: Unlike Arrays, Linked Lists, Stack and queues, which are linear data structures, trees are hierarchical data structures. Binary Tree: A tree whose elements have at most 2 children is called a binary tree. Since each element in a binary tree can have only 2 children, we typically name them the left and right child.
- One reason to use trees might be because you want to store information that naturally forms a hierarchy. For example, the file system on a computer.
- Trees (with some ordering e.g., BST) provide moderate access/search (quicker than Linked List and slower than arrays).
- Trees provide moderate insertion/deletion (quicker than Arrays and slower than Unordered Linked Lists).
- Like Linked Lists and unlike Arrays, Trees don’t have an upper limit on number of nodes as nodes are linked using pointers.
- Store hierarchical data, like folder structure, organization structure, XML/HTML data.
- Binary Search Tree is a tree that allows fast search, insert, delete on a sorted data. It also allows finding closest item
- Heap is a tree data structure which is implemented using arrays and used to implement priority queues.
- B-Tree and B+ Tree : They are used to implement indexing in databases.
- Syntax Tree: Used in Compilers.
- K-D Tree: A space partitioning tree used to organize points in K dimensional space.
- Trie : Used to implement dictionaries with prefix lookup.
- Suffix Tree : For quick pattern searching in a fixed text.
- Spanning Trees and shortest path trees are used in routers and bridges respectively in computer networks
- As a workflow for compositing digital images for visual effects.
A full Binary tree is a special type of binary tree in which every parent node/internal node has either two or no children.
A perfect binary tree is a type of binary tree in which every internal node has exactly two child nodes and all the leaf nodes are at the same level.
A complete binary tree is just like a full binary tree, but with two major differences
- Every level must be completely filled
- All the leaf elements must lean towards the left.
- The last leaf element might not have a right sibling i.e. a complete binary tree doesn't have to be a full binary tree.
A degenerate or pathological tree is the tree having a single child either left or right.
A skewed binary tree is a pathological/degenerate tree in which the tree is either dominated by the left nodes or the right nodes. Thus, there are two types of skewed binary tree: left-skewed binary tree and right-skewed binary tree.
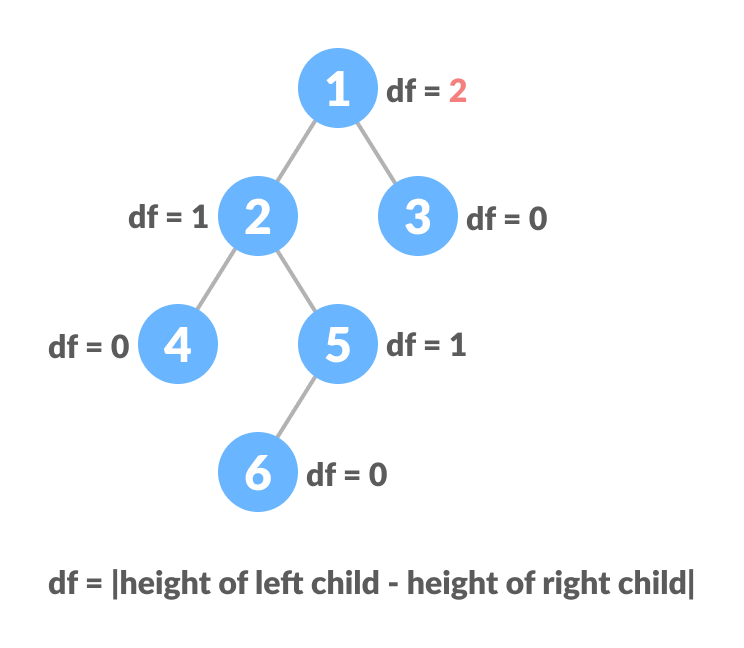
It is a type of binary tree in which the difference between the height of the left and the right subtree for each node is either 0 or 1.
Traversing a tree means visiting every node in the tree. You might, for instance, want to add all the values in the tree or find the largest one. For all these operations, you will need to visit each node of the tree.
Linear data structures like arrays, stacks, queues, and linked list have only one way to read the data. But a hierarchical data structure like a tree can be traversed in different ways.
- First, visit all the nodes in the left subtree
- Then the root node
- Visit all the nodes in the right subtree
inorder(root->left)
display(root->data)
inorder(root->right)
- Visit root node
- Visit all the nodes in the left subtree
- Visit all the nodes in the right subtree
display(root->data)
preorder(root->left)
preorder(root->right)
- Visit all the nodes in the left subtree
- Visit all the nodes in the right subtree
- Visit the root node
postorder(root->left)
postorder(root->right)
display(root->data)
Java language
// Node creation
class Node {
int key;
Node left, right;
public Node(int item) {
key = item;
left = right = null;
}
}
public class BinaryTree {
Node root;
BinaryTree(int key) {
root = new Node(key);
}
BinaryTree() {
root = null;
}
// Traverse Inorder
public void traverseInOrder(Node node) {
if (node != null) {
traverseInOrder(node.left);
System.out.print(" " + node.key);
traverseInOrder(node.right);
}
}
// Traverse Postorder
public void traversePostOrder(Node node) {
if (node != null) {
traversePostOrder(node.left);
traversePostOrder(node.right);
System.out.print(" " + node.key);
}
}
// Traverse Preorder
public void traversePreOrder(Node node) {
if (node != null) {
System.out.print(" " + node.key);
traversePreOrder(node.left);
traversePreOrder(node.right);
}
}
public static void main(String[] args) {
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
System.out.print("Pre order Traversal: ");
tree.traversePreOrder(tree.root);
System.out.print("\nIn order Traversal: ");
tree.traverseInOrder(tree.root);
System.out.print("\nPost order Traversal: ");
tree.traversePostOrder(tree.root);
}
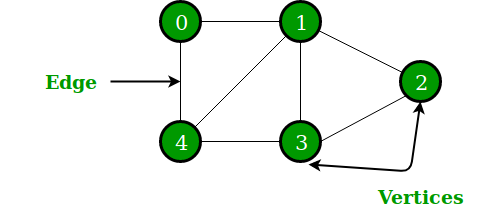
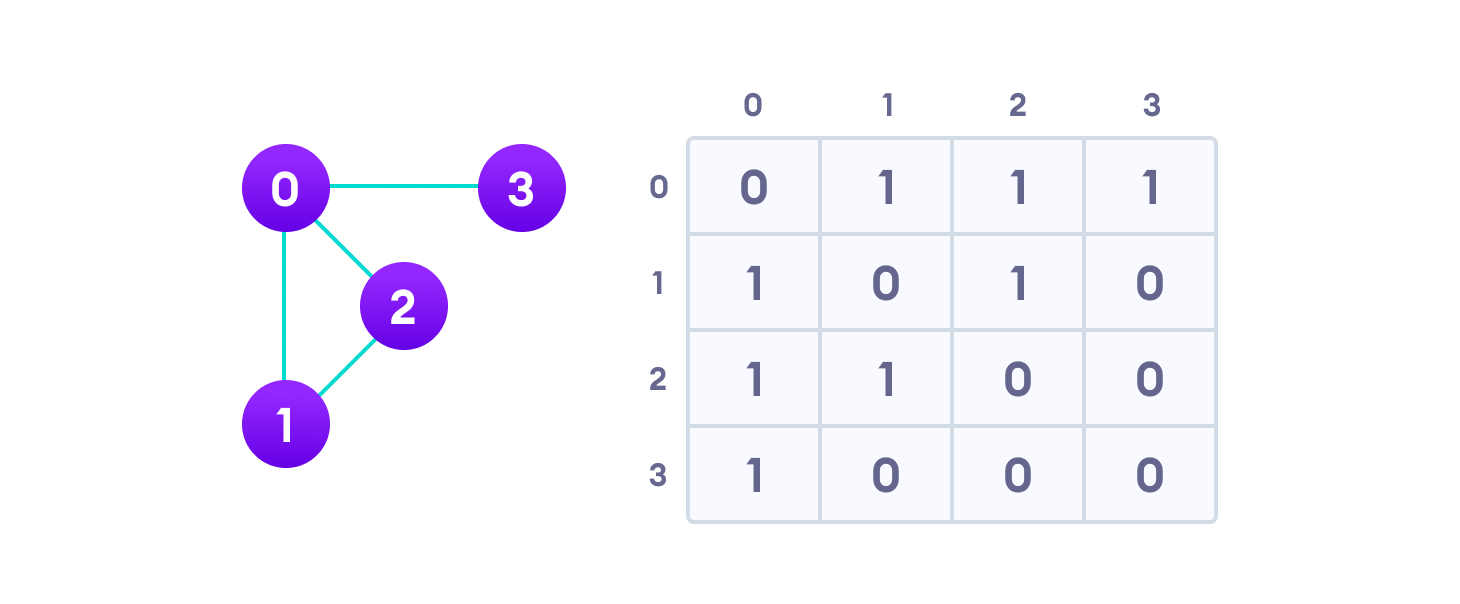
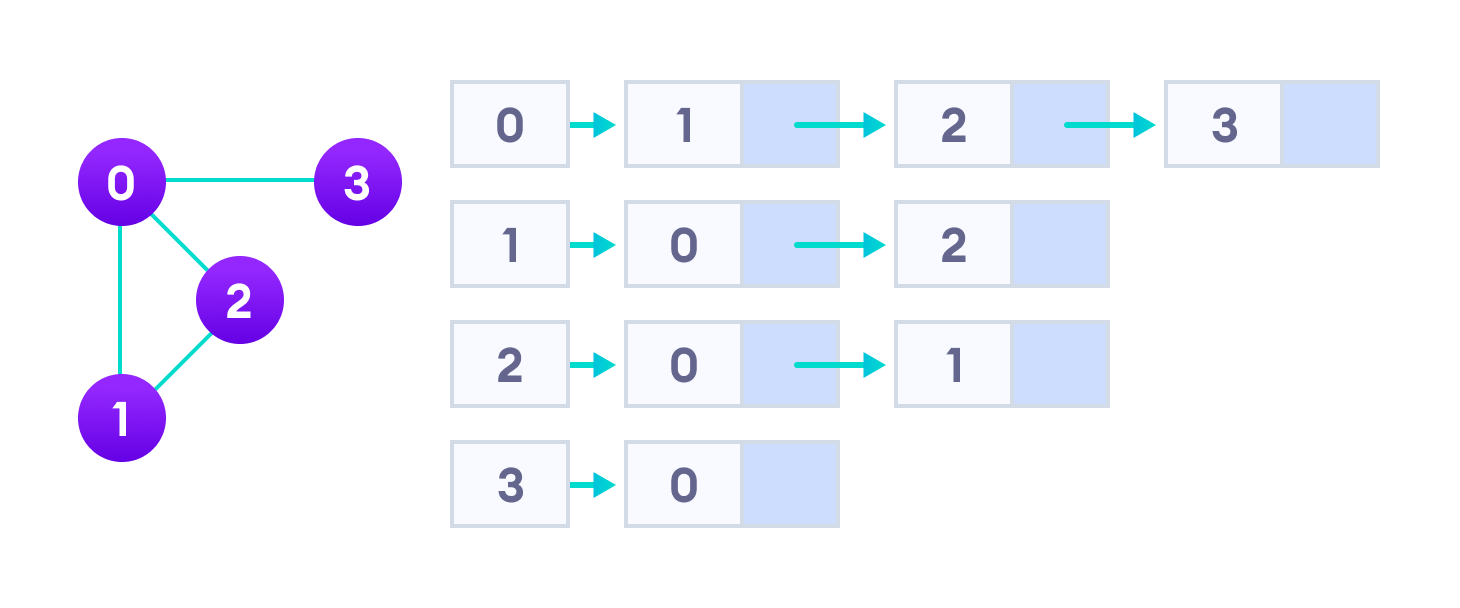
}A Graph is a non-linear data structure consisting of nodes and edges. The nodes are sometimes also referred to as vertices and the edges are lines or arcs that connect any two nodes in the graph.
More precisely, a graph is a data structure (V, E) that consists of
- A collection of vertices V
- A collection of edges E, represented as ordered pairs of vertices (u,v)
V = {0, 1, 2, 3}
E = {(0,1), (0,2), (0,3), (1,2)}
G = {V, E}
- Adjacency: A vertex is said to be adjacent to another vertex if there is an edge connecting them. Vertices 2 and 3 are not adjacent because there is no edge between them.
- Path: A sequence of edges that allows you to go from vertex A to vertex B is called a path. 0-1, 1-2 and 0-2 are paths from vertex 0 to vertex 2.
- Directed Graph: A graph in which an edge (u,v) doesn't necessarily mean that there is an edge (v, u) as well. The edges in such a graph are represented by arrows to show the direction of the edge.
Graphs are commonly represented in two ways:
An adjacency matrix is a 2D array of V x V vertices. Each row and column represent a vertex.
If the value of any element a[i][j] is 1, it represents that there is an edge connecting vertex i and vertex j.
An adjacency list represents a graph as an array of linked lists.
The index of the array represents a vertex and each element in its linked list represents the other vertices that form an edge with the vertex.
The most common graph operations are:
-
Add Vertex − Adds a vertex to the graph.
-
Add Edge − Adds an edge between the two vertices of the graph.
-
Remove Vertex - Removes vertex from the graph.
-
Remove Edge - Removes edge from the graph.
-
Display Vertex − Displays a vertex of the graph.
| Operations | Time complexity |
|---|---|
| Add Vertex | O(1) |
| Add Edge | O(1) |
| Remove Vertex | O(|V| + |E|) |
| Remove Edge | O(|E|) |
| Query | O(|V|) |
Graphs are used to solve many real-life problems. Graphs are used to represent networks. The networks may include paths in a city or telephone network or circuit network. Graphs are also used in social networks like linkedIn, Facebook. For example, in Facebook, each person is represented with a vertex(or node). Each node is a structure and contains information like person id, name, gender, locale etc.
- In Computer science graphs are used to represent the flow of computation.
- Google maps uses graphs for building transportation systems, where intersection of two(or more) roads are considered to be a vertex and the road connecting two vertices is considered to be an edge, thus their navigation system is based on the algorithm to calculate the shortest path between two vertices.
- In Facebook, users are considered to be the vertices and if they are friends then there is an edge running between them. Facebook’s Friend suggestion algorithm uses graph theory. Facebook is an example of undirected graph.
- In World Wide Web, web pages are considered to be the vertices. There is an edge from a page u to other page v if there is a link of page v on page u. This is an example of Directed graph. It was the basic idea behind Google Page Ranking Algorithm.
- In Operating System, we come across the Resource Allocation Graph where each process and resources are considered to be vertices. Edges are drawn from resources to the allocated process, or from requesting process to the requested resource. If this leads to any formation of a cycle then a deadlock will occur.
Java language
import java.util.*;
//class to store edges of the weighted graph
class Edge {
int src, dest, weight;
Edge(int src, int dest, int weight) {
this.src = src;
this.dest = dest;
this.weight = weight;
}
}
// Graph class
class Graph {
// node of adjacency list
static class Node {
int value, weight;
Node(int value, int weight) {
this.value = value;
this.weight = weight;
}
};
// define adjacency list
List<List<Node>> adj_list = new ArrayList<>();
//Graph Constructor
public Graph(List<Edge> edges)
{
// adjacency list memory allocation
for (int i = 0; i < edges.size(); i++)
adj_list.add(i, new ArrayList<>());
// add edges to the graph
for (Edge e : edges)
{
// allocate new node in adjacency List from src to dest
adj_list.get(e.src).add(new Node(e.dest, e.weight));
}
}
// print adjacency list for the graph
public static void printGraph(Graph graph) {
int src_vertex = 0;
int list_size = graph.adj_list.size();
System.out.println("The contents of the graph:");
while (src_vertex < list_size) {
//traverse through the adjacency list and print the edges
for (Node edge : graph.adj_list.get(src_vertex)) {
System.out.print("Vertex:" + src_vertex + " ==> " + edge.value +
" (" + edge.weight + ")\t");
}
System.out.println();
src_vertex++;
}
}
}
public class Main{
public static void main (String[] args) {
// define edges of the graph
List<Edge> edges = Arrays.asList(new Edge(0, 1, 2),new Edge(0, 2, 4),
new Edge(1, 2, 4),new Edge(2, 0, 5), new Edge(2, 1, 4),
new Edge(3, 2, 3), new Edge(4, 5, 1),new Edge(5, 4, 3));
// call graph class Constructor to construct a graph
Graph graph = new Graph(edges);
// print the graph as an adjacency list
Graph.printGraph(graph);
}
}A Hash Table is a data structure that stores values which have keys associated with each of them. Furthermore, it supports lookup efficiently if we know the key associated with the value (It is very fast in serching the data). Hence it is very efficient in inserting and searching, irrespective of the size of the data.
The Hash table data structure stores elements in key-value pairs where
- Key- unique integer that is used for indexing the values
- Value - data that are associated with keys.
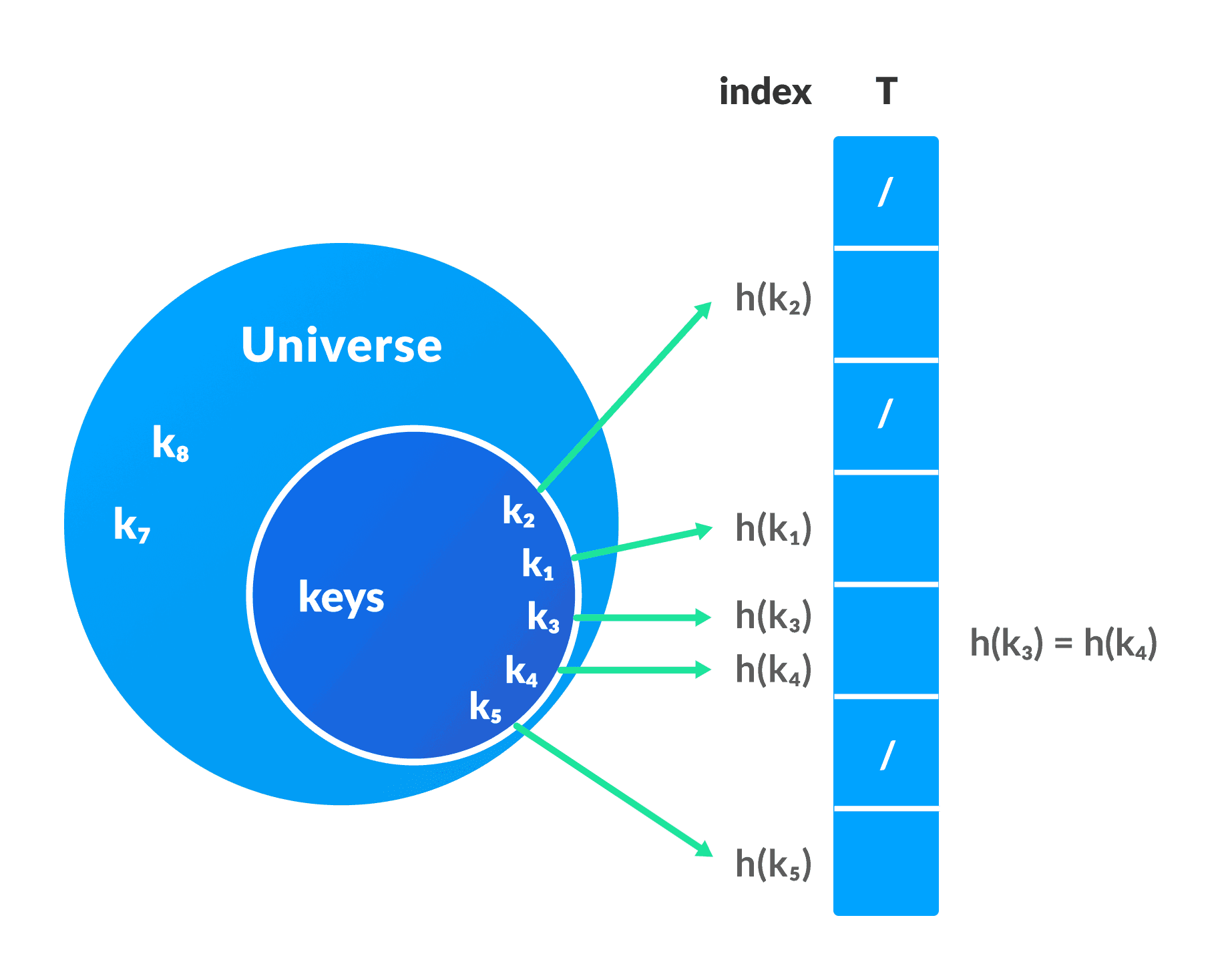
Hashing is a technique to convert a range of key values into a range of indexes of an array. In a hash table, a new index is processed using the keys. And, the element corresponding to that key is stored in the index. This process is called hashing.
Let k be a key and h(x) be a hash function.
Here, h(k) will give us a new index to store the element linked with k.
When the hash function generates the same index for multiple keys, there will be a conflict (what value to be stored in that index). This is called a hash collision.
We can resolve the hash collision using one of the following techniques.
- Collision resolution by chaining
- Open Addressing: Linear/Quadratic Probing and Double Hashing
In chaining, if a hash function produces the same index for multiple elements, these elements are stored in the same index by using a doubly-linked list.
If j is the slot for multiple elements, it contains a pointer to the head of the list of elements. If no element is present, j contains NIL.
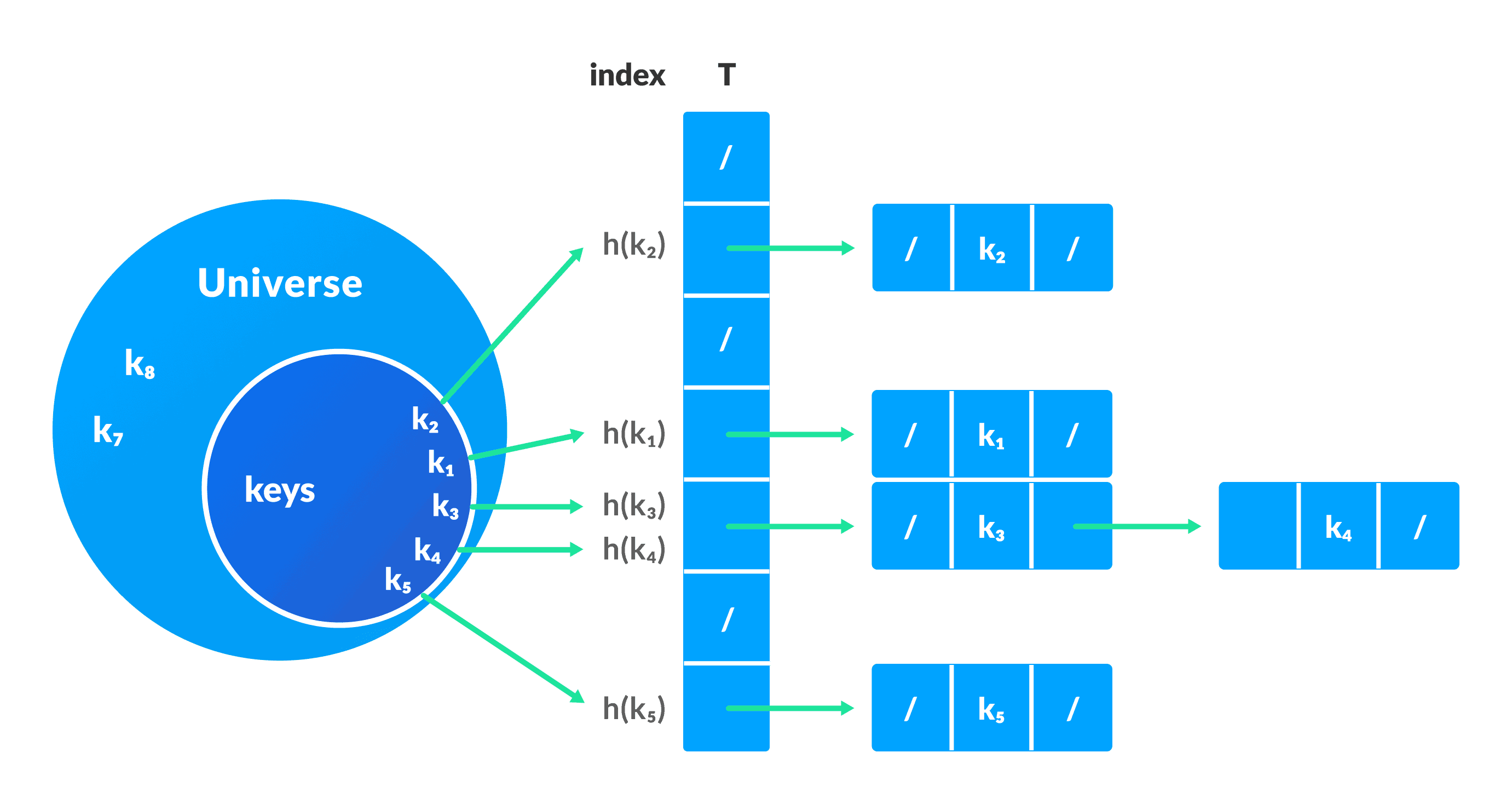
chainedHashSearch(T, k)
return T[h(k)]
chainedHashInsert(T, x)
T[h(x.key)] = x //insert at the head
chainedHashDelete(T, x)
T[h(x.key)] = NIL
-
search() − Searches an element in a hash table.
-
insert() − inserts an element in a hash table.
-
delete() − Deletes an element from a hash table.
| Operation | Time Complexity |
|---|---|
| search() | O(1) |
| insert() | O(1) |
| delete() | O(1) |
Hash tables are implemented where
- constant time lookup and insertion is required
- cryptographic applications
- indexing data is required
Implementation of Hash Table in Java (Chaining example)
Java langauge
// Java program to demonstrate implementation of our
// own hash table with chaining for collision detection
import java.util.ArrayList;
// A node of chains
class HashNode<K, V> {
K key;
V value;
// Reference to next node
HashNode<K, V> next;
// Constructor
public HashNode(K key, V value)
{
this.key = key;
this.value = value;
}
}
// Class to represent entire hash table
public class Map<K, V> {
// bucketArray is used to store array of chains
private ArrayList<HashNode<K, V> > bucketArray;
// Current capacity of array list
private int numBuckets;
// Current size of array list
private int size;
// Constructor (Initializes capacity, size and
// empty chains.
public Map()
{
bucketArray = new ArrayList<>();
numBuckets = 10;
size = 0;
// Create empty chains
for (int i = 0; i < numBuckets; i++)
bucketArray.add(null);
}
public int size() { return size; }
public boolean isEmpty() { return size() == 0; }
// This implements hash function to find index
// for a key
private int getBucketIndex(K key)
{
int hashCode = key.hashCode();
int index = hashCode % numBuckets;
// key.hashCode() coule be negative.
index = index < 0 ? index * -1 : index;
return index;
}
// Method to remove a given key
public V remove(K key)
{
// Apply hash function to find index for given key
int bucketIndex = getBucketIndex(key);
// Get head of chain
HashNode<K, V> head = bucketArray.get(bucketIndex);
// Search for key in its chain
HashNode<K, V> prev = null;
while (head != null) {
// If Key found
if (head.key.equals(key))
break;
// Else keep moving in chain
prev = head;
head = head.next;
}
// If key was not there
if (head == null)
return null;
// Reduce size
size--;
// Remove key
if (prev != null)
prev.next = head.next;
else
bucketArray.set(bucketIndex, head.next);
return head.value;
}
// Returns value for a key
public V get(K key)
{
// Find head of chain for given key
int bucketIndex = getBucketIndex(key);
HashNode<K, V> head = bucketArray.get(bucketIndex);
// Search key in chain
while (head != null) {
if (head.key.equals(key))
return head.value;
head = head.next;
}
// If key not found
return null;
}
// Adds a key value pair to hash
public void add(K key, V value)
{
// Find head of chain for given key
int bucketIndex = getBucketIndex(key);
HashNode<K, V> head = bucketArray.get(bucketIndex);
// Check if key is already present
while (head != null) {
if (head.key.equals(key)) {
head.value = value;
return;
}
head = head.next;
}
// Insert key in chain
size++;
head = bucketArray.get(bucketIndex);
HashNode<K, V> newNode
= new HashNode<K, V>(key, value);
newNode.next = head;
bucketArray.set(bucketIndex, newNode);
// If load factor goes beyond threshold, then
// double hash table size
if ((1.0 * size) / numBuckets >= 0.7) {
ArrayList<HashNode<K, V> > temp = bucketArray;
bucketArray = new ArrayList<>();
numBuckets = 2 * numBuckets;
size = 0;
for (int i = 0; i < numBuckets; i++)
bucketArray.add(null);
for (HashNode<K, V> headNode : temp) {
while (headNode != null) {
add(headNode.key, headNode.value);
headNode = headNode.next;
}
}
}
}
// Driver method to test Map class
public static void main(String[] args)
{
Map<String, Integer> map = new Map<>();
map.add("this", 1);
map.add("coder", 2);
map.add("this", 4);
map.add("hi", 5);
System.out.println(map.size());
System.out.println(map.remove("this"));
System.out.println(map.remove("this"));
System.out.println(map.size());
System.out.println(map.isEmpty());
}
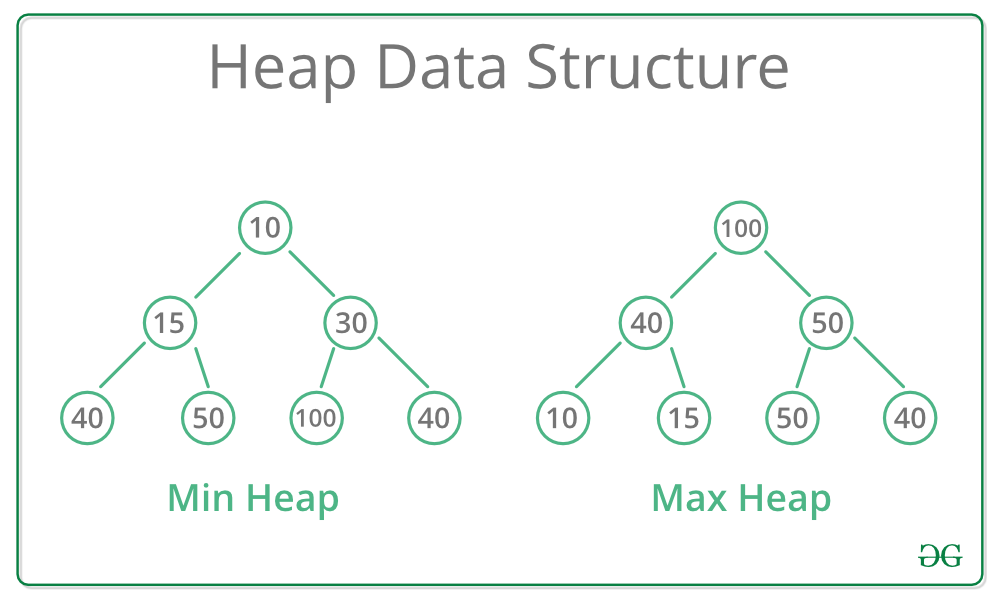
}A Heap is a special Tree-based data structure in which the tree is a complete binary tree. Heap is one maximally efficient implementation of an abstract data type called a priority queue. It is also called as a binary heap.
Generally, Heaps can be of two types:
- Max-Heap: In a Max-Heap the key present at the root node must be greatest among the keys present at all of it’s children. The same property must be recursively true for all sub-trees in that Binary Tree.
- Min-Heap: In a Min-Heap the key present at the root node must be minimum among the keys present at all of it’s children. The same property must be recursively true for all sub-trees in that Binary Tree.
A binary heap is typically represented as an array.
- The root element will be at Arr[0].
- Below table shows indexes of other nodes for the i'th node, i.e., Arr[i]:
Arr[(i-1)/2] Returns the parent node
Arr[(2*i)+1] Returns the left child node
Arr[(2*i)+2] Returns the right child node
- Heap Sort: Heap Sort uses Binary Heap to sort an array in O(nLogn) time
- Priority Queue: Priority queues can be efficiently implemented using Binary Heap because it supports insert(), delete() and extractmax(), decreaseKey() operations in O(logn) time. Binomoial Heap and Fibonacci Heap are variations of Binary Heap. These variations perform union also efficiently.
- Graph Algorithms: The priority queues are especially used in Graph Algorithms like Dijkstra’s Shortest Path and Prim’s Minimum Spanning Tree.
- Many problems can be efficiently solved using Heaps.
a) K’th Largest Element in an array.
b) Sort an almost sorted array/
c) Merge K Sorted Arrays.
For Max Heap is similar, only vice versa
-
getMini(): It returns the root element of Min Heap.
-
extractMin(): Removes the minimum element from MinHeap.
-
decreaseKey(): Decreases value of key. If the decreases key value of a node is greater than the parent of the node, then we don’t need to do anything. Otherwise, we need to traverse up to fix the violated heap property.
-
insert(): We add a new key at the end of the tree. IF new key is greater than its parent, then we don’t need to do anything. Otherwise, we need to traverse up to fix the violated heap property.
-
delete(): We replace the key to be deleted with minum infinite by calling decreaseKey(). After decreaseKey(), the minus infinite value must reach root, so we call extractMin() to remove the key.
| operation | Time Complexity |
|---|---|
| getMin() | O(1) |
| extractMin() | O(logn) |
| decreaseKey() | O(logn) |
| insert() | O(logn) |
| delete() | O(logn) |
// Java implementation of Min Heap
public class MinHeap {
private int[] Heap;
private int size;
private int maxsize;
private static final int FRONT = 1;
public MinHeap(int maxsize)
{
this.maxsize = maxsize;
this.size = 0;
Heap = new int[this.maxsize + 1];
Heap[0] = Integer.MIN_VALUE;
}
// Function to return the position of
// the parent for the node currently
// at pos
private int parent(int pos)
{
return pos / 2;
}
// Function to return the position of the
// left child for the node currently at pos
private int leftChild(int pos)
{
return (2 * pos);
}
// Function to return the position of
// the right child for the node currently
// at pos
private int rightChild(int pos)
{
return (2 * pos) + 1;
}
// Function that returns true if the passed
// node is a leaf node
private boolean isLeaf(int pos)
{
if (pos >= (size / 2) && pos <= size) {
return true;
}
return false;
}
// Function to swap two nodes of the heap
private void swap(int fpos, int spos)
{
int tmp;
tmp = Heap[fpos];
Heap[fpos] = Heap[spos];
Heap[spos] = tmp;
}
// Function to heapify the node at pos
private void minHeapify(int pos)
{
// If the node is a non-leaf node and greater
// than any of its child
if (!isLeaf(pos)) {
if (Heap[pos] > Heap[leftChild(pos)]
|| Heap[pos] > Heap[rightChild(pos)]) {
// Swap with the left child and heapify
// the left child
if (Heap[leftChild(pos)] < Heap[rightChild(pos)]) {
swap(pos, leftChild(pos));
minHeapify(leftChild(pos));
}
// Swap with the right child and heapify
// the right child
else {
swap(pos, rightChild(pos));
minHeapify(rightChild(pos));
}
}
}
}
// Function to insert a node into the heap
public void insert(int element)
{
if (size >= maxsize) {
return;
}
Heap[++size] = element;
int current = size;
while (Heap[current] < Heap[parent(current)]) {
swap(current, parent(current));
current = parent(current);
}
}
// Function to print the contents of the heap
public void print()
{
for (int i = 1; i <= size / 2; i++) {
System.out.print(" PARENT : " + Heap[i]
+ " LEFT CHILD : " + Heap[2 * i]
+ " RIGHT CHILD :" + Heap[2 * i + 1]);
System.out.println();
}
}
// Function to build the min heap using
// the minHeapify
public void minHeap()
{
for (int pos = (size / 2); pos >= 1; pos--) {
minHeapify(pos);
}
}
// Function to remove and return the minimum
// element from the heap
public int remove()
{
int popped = Heap[FRONT];
Heap[FRONT] = Heap[size--];
minHeapify(FRONT);
return popped;
}
// Driver code
public static void main(String[] arg)
{
System.out.println("The Min Heap is ");
MinHeap minHeap = new MinHeap(15);
minHeap.insert(5);
minHeap.insert(3);
minHeap.insert(17);
minHeap.insert(10);
minHeap.insert(84);
minHeap.insert(19);
minHeap.insert(6);
minHeap.insert(22);
minHeap.insert(9);
minHeap.minHeap();
minHeap.print();
System.out.println("The Min val is " + minHeap.remove());
}
}