Recursive vs. NonRecursive Counter - A Practical Analysis

---

This repository is part of a series of basic implementations that I'm going to persist in this platform as a personal reference of how to design certain algorithms.

A n-charaters length word based on m-elements alphabet counter is sometimes a very useful tool to solve certain kind of problems.

For example, we are all familiar with permutations of 0's and 1's:

0	0	0
0	0	1
0	1	0
0	1	1
1	0	0
1	0	1
1	1	0
1	1	1

(alphabet = 2 elements [0,1]; word = 3 characters length; alphabet^word = 8 permutations)

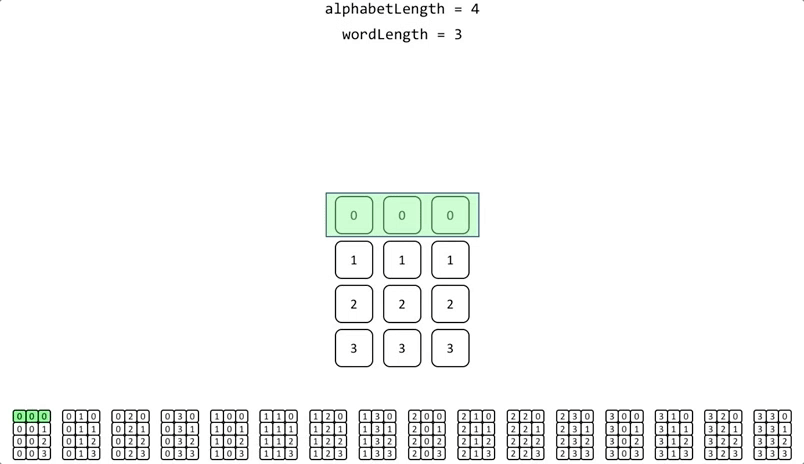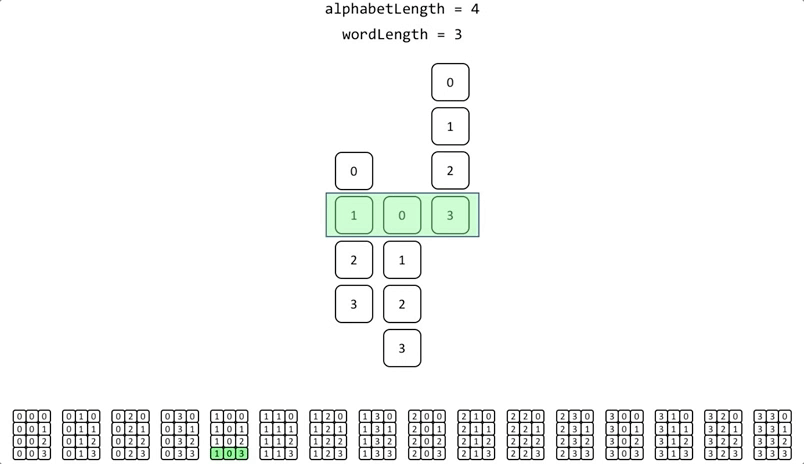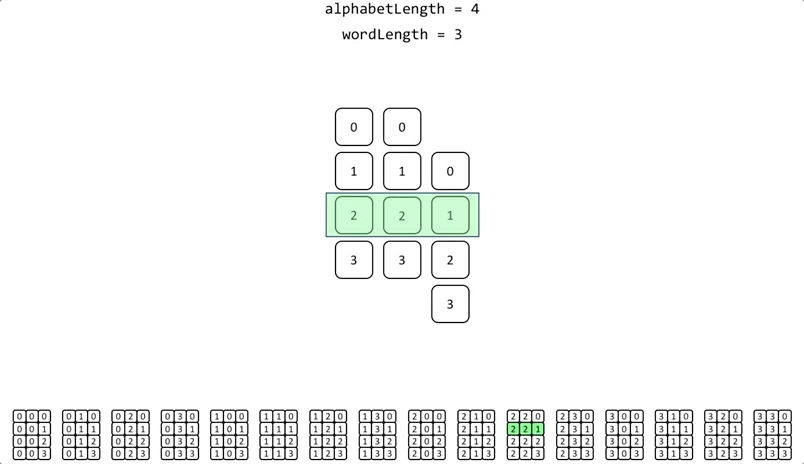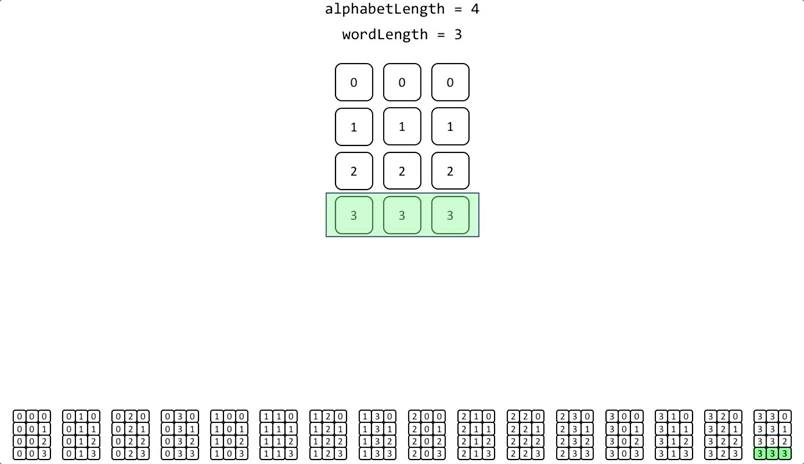
But, what if we need base 4 permutations of the same length?. It would look like this:

0	0	0
0	0	1
0	0	2
0	0	3
0	1	0
0	1	1
0	1	2
0	1	3
0	2	0
...	...	...
3	3	0
3	3	1
3	3	2
3	3	3

(alphabet = 4 elements [0,1,2,3]; word = 3 characters length; alphabet^word = 64 permutations)

Well, there are two basic ways to implement this. The "easy" one is using recursion, and the less intuitive using traditional loops.

Let's have a look of booth methods.

Implementation of a generic counter using Recursion

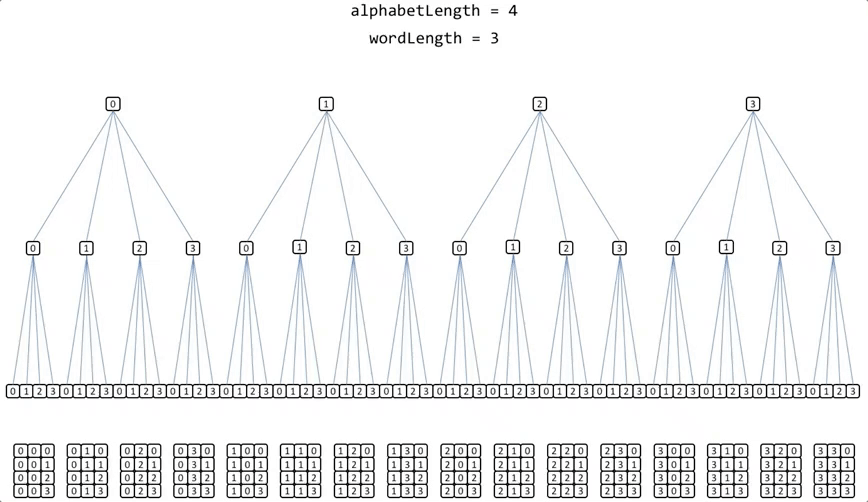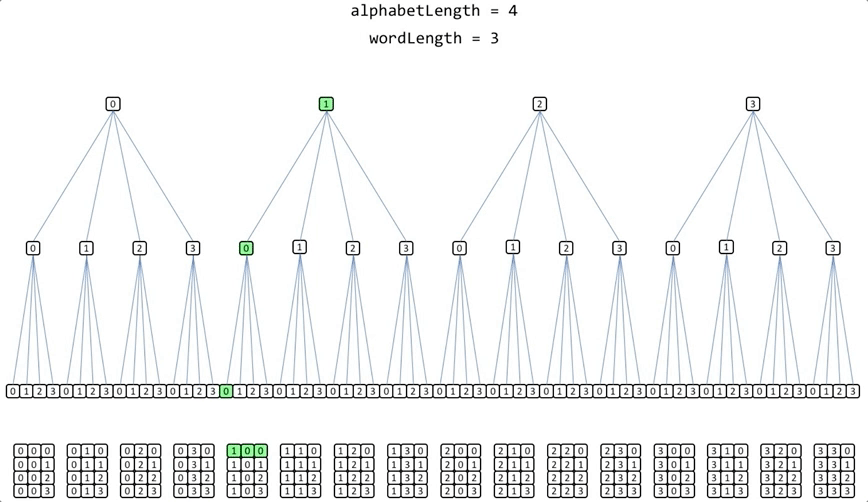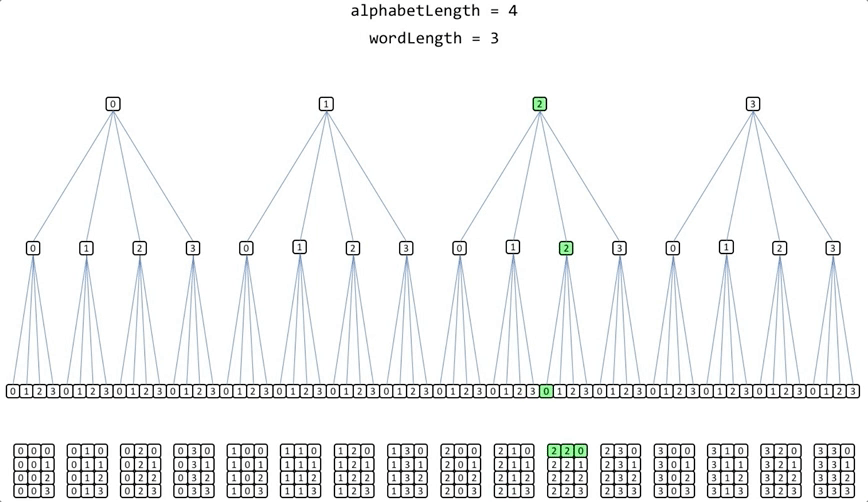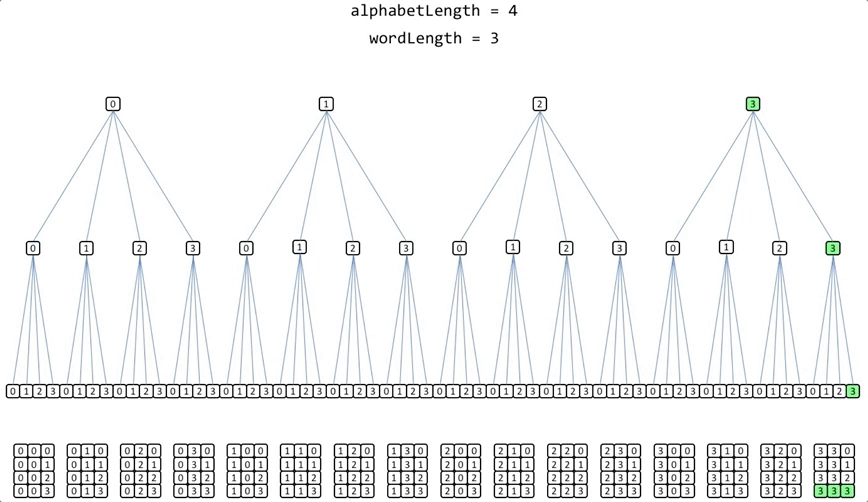
The previous example of permutations using an alphabet of 4 elements [0,1,2,3]; and a word length = 3, if recursion is used the execution of the algorithm would look like this:

The implementation is very simple:

static void genericCounterRecursive(int level, int maxLevel, int[] sequence) {
    if (level == 0) {
        /*word completed, do something with it.*/
        return;
    }
    for (int i=0; i<alphabet.length; i++) {
        sequence[maxLevel - level] = alphabet[i];
        genericCounterRecursive(level-1, maxLevel, sequence);
    }
}

Implementation of a generic counter using simple loops

On the other hand, if we try to solve this using simple loops, the implementation is a little tricky:

static void genericCounterNonRecursive(int maxLevel, int[] sequence) {
    /*first word, do something with it.*/
    int alphaLen = alphabet.length - 1;
    int ptr = 0;
    while (ptr >= 0) {
        ptr = maxLevel;
        if (sequence[maxLevel] < alphaLen) {
            sequence[maxLevel]++;
            /*word completed, do something with it.*/
        } else {
            while (ptr >= 0 && sequence[ptr] == alphaLen) {
                sequence[ptr] = 0;
                ptr--;
            }
            if (ptr >= 0 && sequence[ptr] < alphaLen) {
                sequence[ptr]++;
                /*word completed, do something with it.*/
            }
        }			
    }
}

However, the execution looks simpler:

Comparision

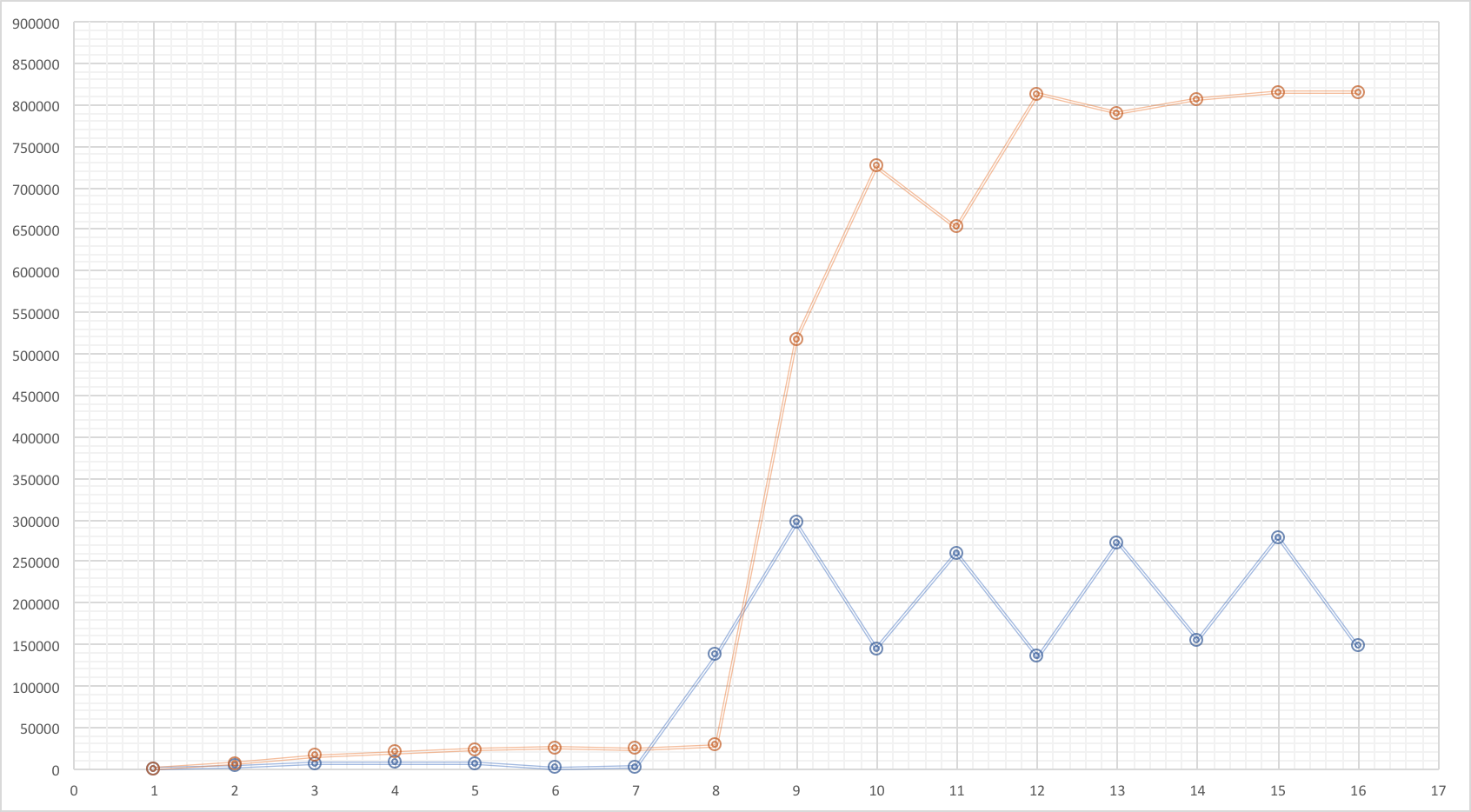
There is a huge difference between the two methods in terms of execution time.

The blue line represents the amount of permutations generated per millisecond for different characters length words, using recursion.

The orange line represents the amount of permutations generated per millisecond for different characters length words, using simple loops.

As you can see, for 8 or less characters length words, the execution time is more or less the same for both methods, but for larger words, the simple loops method is FAR faster generating permutations (more than 800,000 permutations per millisecond, compared to the 200,000 on avg using recursion).

Conclusion

Although recursion leads to cleaner code and simpler debugging, sometimes is not necessarily the more efficient method to address a problem.

Compiling, Packaging and Executing the software

There is a script named compile.sh that you can use in order to compile and package the project. Or, just execute the following command: mvn clean compile assembly:single.

The JAR file is created at counter/target, just execute a java -jar <jar file generated>

Possible Next Steps

Parallel Processing perhaps?, A comparision among different programming languages would be nice also.