<Projects like this one are prototypes, that means that special attention was given to the problem itself rather than having a perfect software design.>
In professional software development, we don’t find algorithmically challenging problems so often. Sure, there are a lot of complex projects out there, but we must remember that despite the knowledge that we might have on a particular set of technologies, we also need to constantly polish our algorithm design skills.
Having this in mind, I came across this puzzle and ask myself, how would I instruct a computer to find all possible solutions to this? Let’s find out.
First of all, how would a human solve it? I guess that for a problem like this, a great majority of people would just try one piece at a time in a trial-and-error way. So, if I were to solve this myself, I would use the following procedure:
- Starting from the upper left corner, from left to right, top down. (Or the lower right corner, it doesn’t really matter, what matters is that we decide to start somewhere in the puzzle and stick to our decision):
- 1) Piece number 1 (whatever piece we decide), is placed in the upper left corner.
- 2) In the spaces that are left, can we put another piece?
- 3) NO, rotate 90 degrees clockwise/counter-clockwise, or flip horizontally/vertically (or, in other words, try a different position) and try again (go to step 2)).
- 4) YES, let’s continue with the following piece (piece number 2).
- 4.1) In the spaces that are left, can we put another piece? (except piece number 1 because is already placed).
- 4.2) NO, rotate 90 degrees clockwise/counter-clockwise, or flip horizontally/vertically and try again (go to step 4.1))
- 4.3) YES, let’s continue with the following piece (piece number 3).
- 4.3.1) In the spaces that are left, can we put another piece? (except piece number 1 and 2 because they are already placed)
- 4.3.2) NO, rotate 90 degrees clockwise/counter-clockwise, or flip horizontally/vertically and try again (go to step 4.3.1))
- 4.3.3) YES, let’s continue with the following piece (piece number 4).
- 4.3.3.1) And so on...
See where this is going?
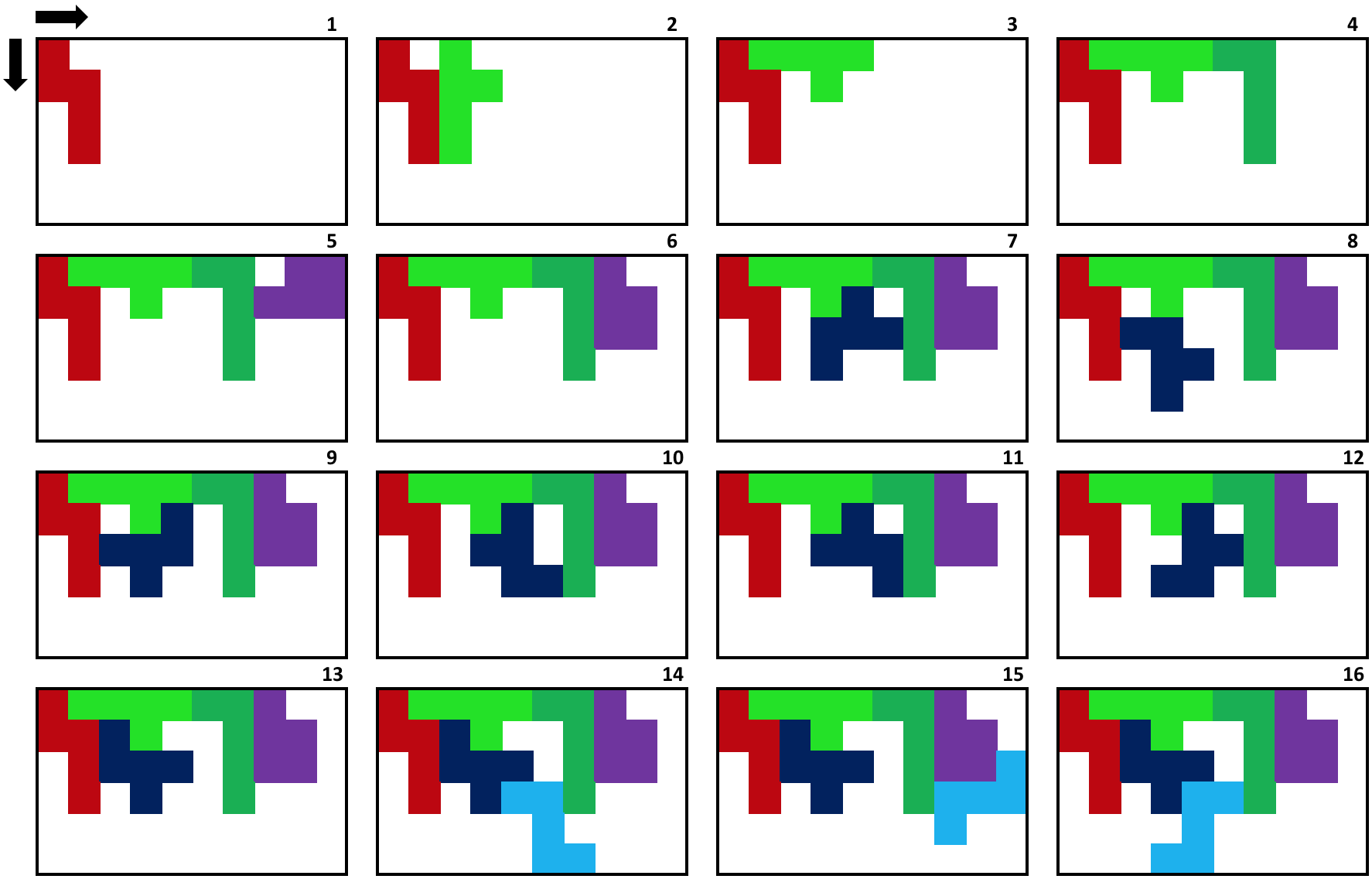
Let’s execute the algorithm, but now visually:
- Step 1: in the diagram: Piece number 1 is placed in the upper left corner and, there is still plenty of space left for the next piece.
- Step 2: Piece number 2 is placed, but there is a little hole where no other piece can fit. So, we change the position of the piece (rotate clockwise in this case) and try again.
- Step 3: Piece number 2 is placed in a new position and now we have space left to continue.
- Step 4: Piece number 3 is placed and we still have space left to continue.
- Step 5: Piece number 4 is placed but there is a little hole where no other piece can fit. So, we change the position of the piece (rotate clockwise) and try again.
- Step 6: Piece number 4 is placed in a new position and we have space left to continue.
- And so on…
We have now an algorithm that can help us find solutions to this puzzle, let’s translate it into something that a computer can understand.
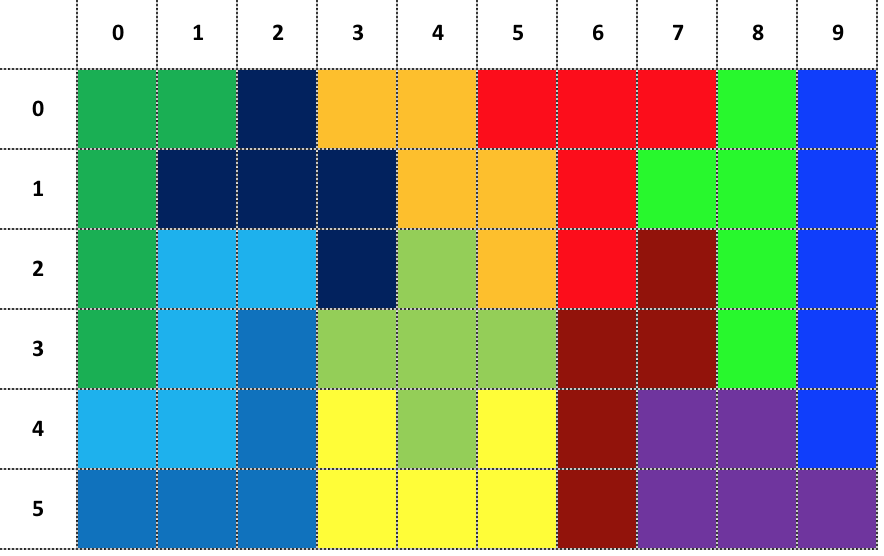
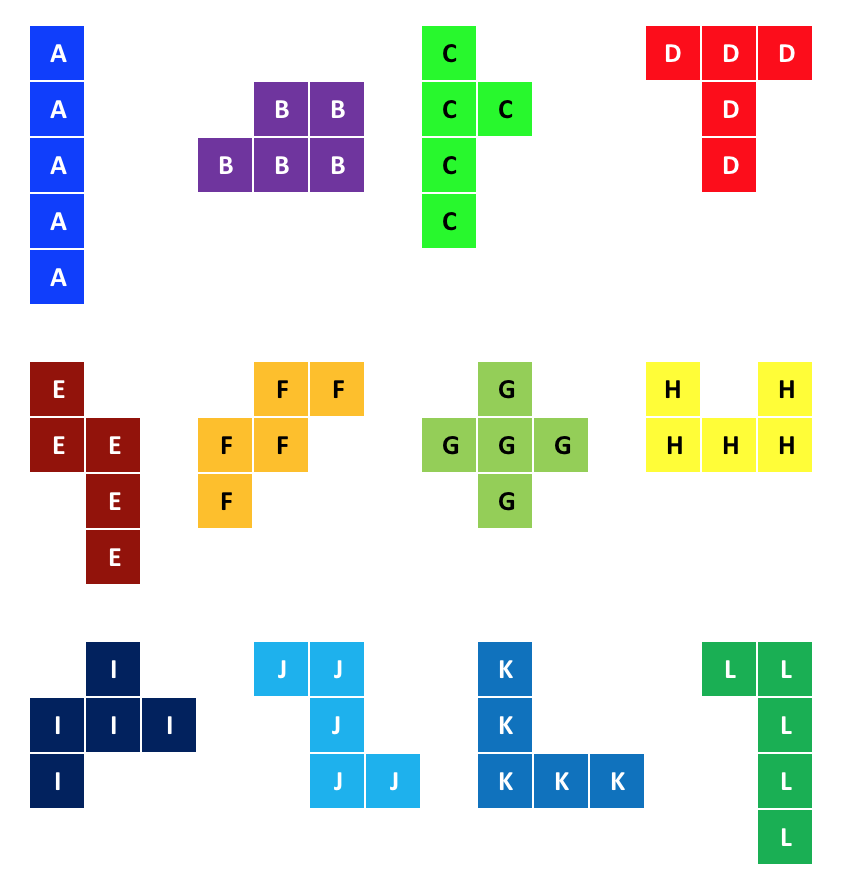
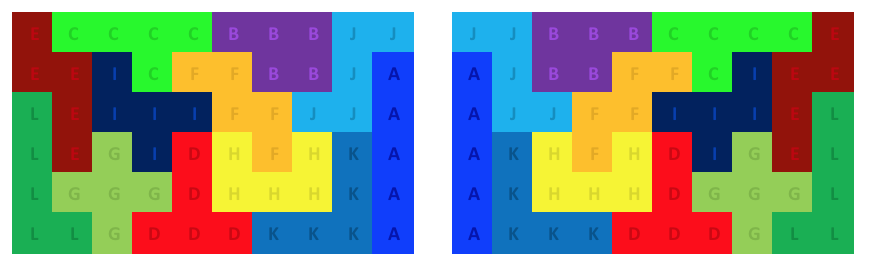
How can we define a “Piece” in computer terms? First, the puzzle must be broken down into smaller components, in this case the pieces are made of 5 squares each for a total of 12 pieces that fit in a 6 x 10 squares space (60 squares)
We can identify each piece with a letter from the alphabet:
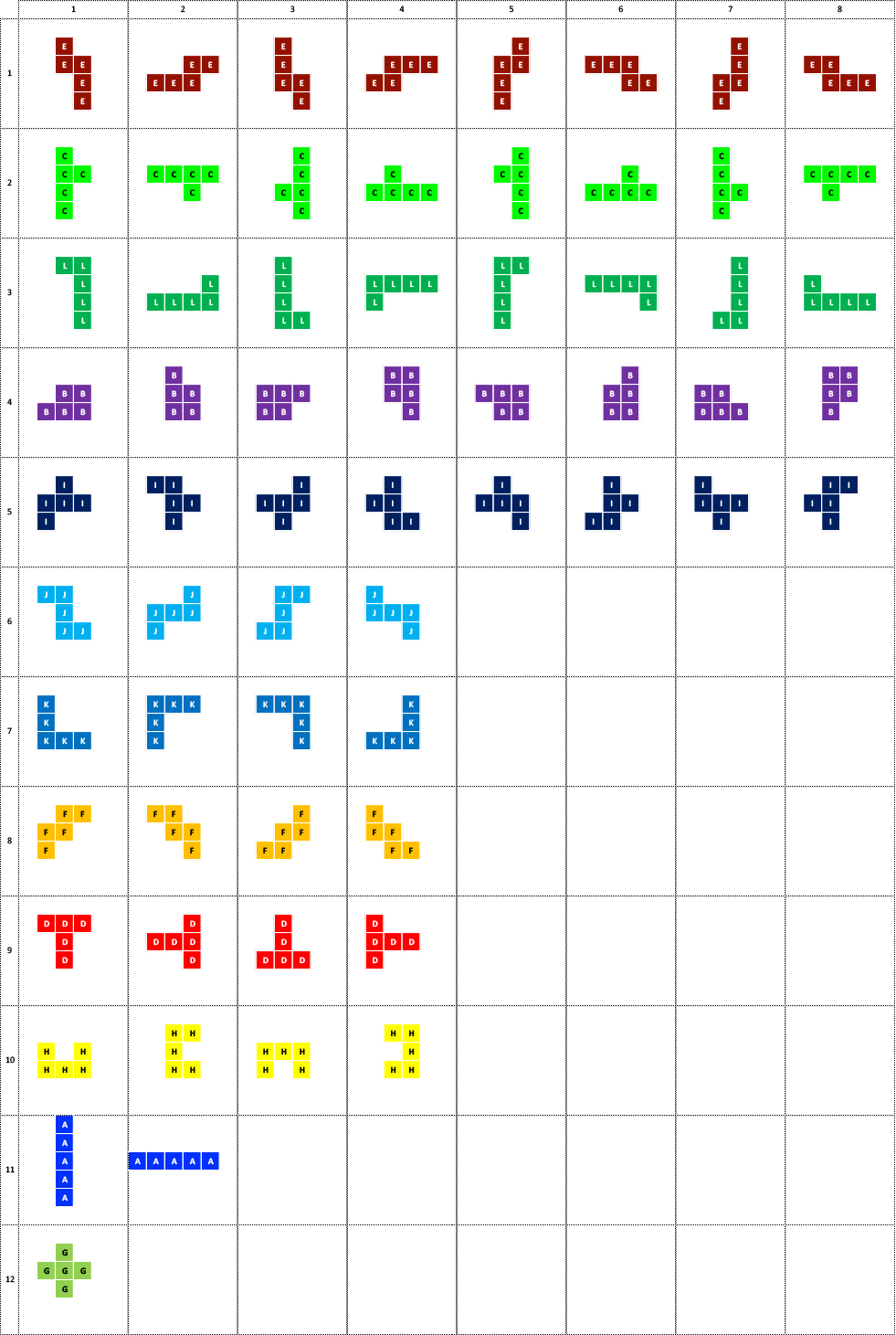
Now, each one of these pieces can fit in the 6x10 space in different positions (except piece G as you may have noticed already), let's put in an array all these different positions:
The order of the pieces doesn't really matter for the purpose of creating a program that can find all possible solutions to this puzzle. We are using Java as the programming language to solve this problem, so let’s define all these combinations of pieces and different positions in Java terms.
I have defined 2 java classes: Piece.java and PieceConfig.Java, the former is self-explained, the latter represents the different positions a piece could be placed within the puzzle board.
To define a Piece and its different positions (PieceConfig objects) we do it the following way:
/* +---+---+
| E | E |
+---+---+---+---+
| E | E | E |
+---+---+---+ */
Piece p_E = new Piece(1,"E");
p_E.getPieceConfigurations().add(new PieceConfig(1,p_E,
new int[][]{{1,0},
{1,1},
{0,1},
{0,1}}, 4, 2)
);
p_E.getPieceConfigurations().add(new PieceConfig(2,p_E,
new int[][]{{0,0,1,1},
{1,1,1,0}}, 2, 4)
);
p_E.getPieceConfigurations().add(new PieceConfig(3,p_E,
new int[][]{{1,0},
{1,0},
{1,1},
{0,1}}, 4, 2)
);
p_E.getPieceConfigurations().add(new PieceConfig(4,p_E,
new int[][]{{0,1,1,1},
{1,1,0,0}}, 2, 4)
);
p_E.getPieceConfigurations().add(new PieceConfig(5,p_E,
new int[][]{{0,1},
{1,1},
{1,0},
{1,0}}, 4, 2)
);
p_E.getPieceConfigurations().add(new PieceConfig(6,p_E,
new int[][]{{1,1,1,0},
{0,0,1,1}}, 2, 4)
);
p_E.getPieceConfigurations().add(new PieceConfig(7,p_E,
new int[][]{{0,1},
{0,1},
{1,1},
{1,0}}, 4, 2)
);
p_E.getPieceConfigurations().add(new PieceConfig(8,p_E,
new int[][]{{1,1,0,0},
{0,1,1,1}}, 2, 4)
);
PIECES.add(p_E);As you perhaps have already noticed, the different positions (or configurations) this piece can be, are defined within those little arrays of 0’s and 1’s. In the last line of code of this sample, we add the piece (and its configurations) to a larger array along with the rest of the pieces.
Now that we have a data structure where we can find all the different pieces and their different positions (configurations), let’s write the main piece of code in charge of trying every possible combination of pieces and positions:
solvePuzzle(Piece p, PieceConfiguration config) {
if (!areThereIncompatibleSpaces()) {
if (tryToPutPieceIntoPlayground(p, config)) {
if (!isPuzzleSolved()) {
for (Piece pp: PIECES) {
if (!isPieceAlreadyInPlayground(pp)) {
for (PieceConfig pConfig: pp.getPieceConfigurations()) {
solvePuzzle(pp, pConfig);
}
}
}
} else {
registerSolution();
}
}
}
}
main(String[] args) {
loadAllPieces();
for (Piece p: PIECES) {
for (PieceConfiguration config: p. getPieceConfigurations ()) {
solvePuzzle(p, config);
}
}
}What the above code says is:
- 1) All the Pieces and their possible positions are loaded into a data structure called PIECES (We already talked about this).
- 2) For every Piece, and for every Piece's possible position, invoke something called "solvePuzzle".
- 3) Within "solvePuzzle":
- 3.1) Check if there are NOT “incompatible spaces” (spaces where no piece could fit). If successful go to step 3.3), if not, go to step 3.2).
- 3.2) "solvePuzzle" ends.
- 3.3) Try to put a piece into the puzzle board. If successful go to step 3.5), if not, go to step 3.4).
- 3.4) "solvePuzzle" ends.
- 3.5) Check if the Puzzle is NOT solved. If is not, go to step 3.7), otherwise, go to step 3.6).
- 3.6) "solvePuzzle" registers solution and ends.
- 3.7) For every Piece NOT PLACED in the puzzle board, and for every Piece's possible position (configuration), invoke something called "solvePuzzle".
Let’s break into smaller pieces each one of the steps that are not obvious from a programming perspective.
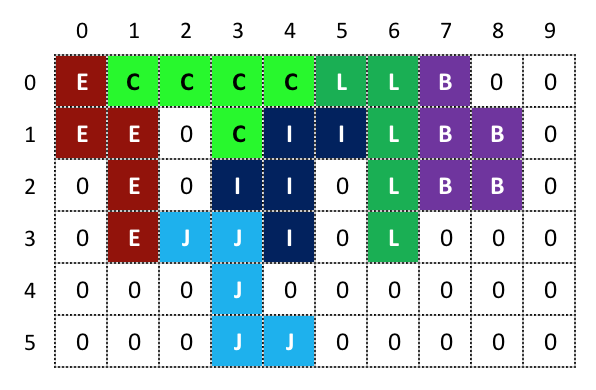
Let’s begin explaining this with an example. Suppose that after several computations of the algorithm, we have the following state:
Here there are 3 "areas" in which we could place additional pieces, but, there is one where no piece could fit ([row: 1, col: 2] to [row: 2, col: 2]).
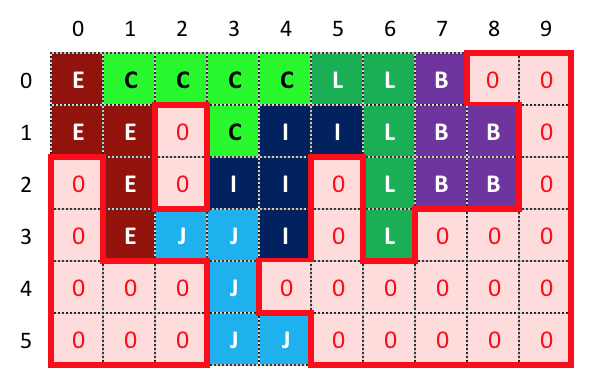
In order to tell a computer how to spot these “areas”, we borrow a technique from image processing called Region Growing.
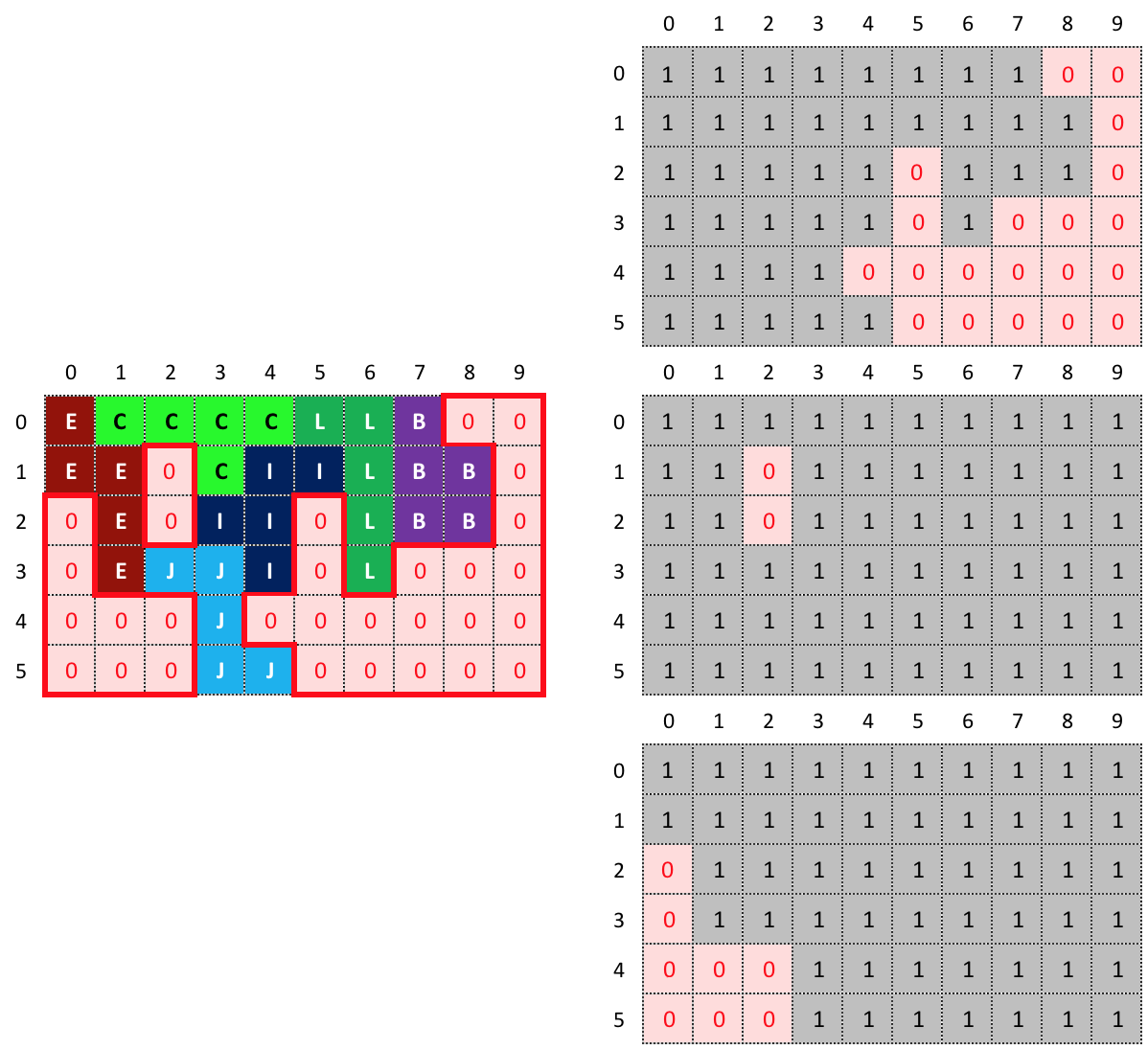
What we do basically is iterate along the puzzle board (an array 6x10 in size, made of 0’s and 1’s) and when we find a 0 (zero, or an “empty space”) we perform a recursive call on the “neighborhood” (the 4 cells, to the left, right, up and down of the current cell) and then repeat the process until no other 0 (zero, or an “empty space”) is found. (Within the code this is the XRay.java class). What we end up with is a collection of arrays that are as many as isolated areas are found:
And when we try to place pieces within these arrays with isolated areas, we test if those fit. If at least ONE “area” is no place for all the pieces that are not already placed in the puzzle board, then the whole solution path is discarded because is taking nowhere.
In this example, such array is in the middle with the isolated “area” made of 2 squares as I mentioned before.
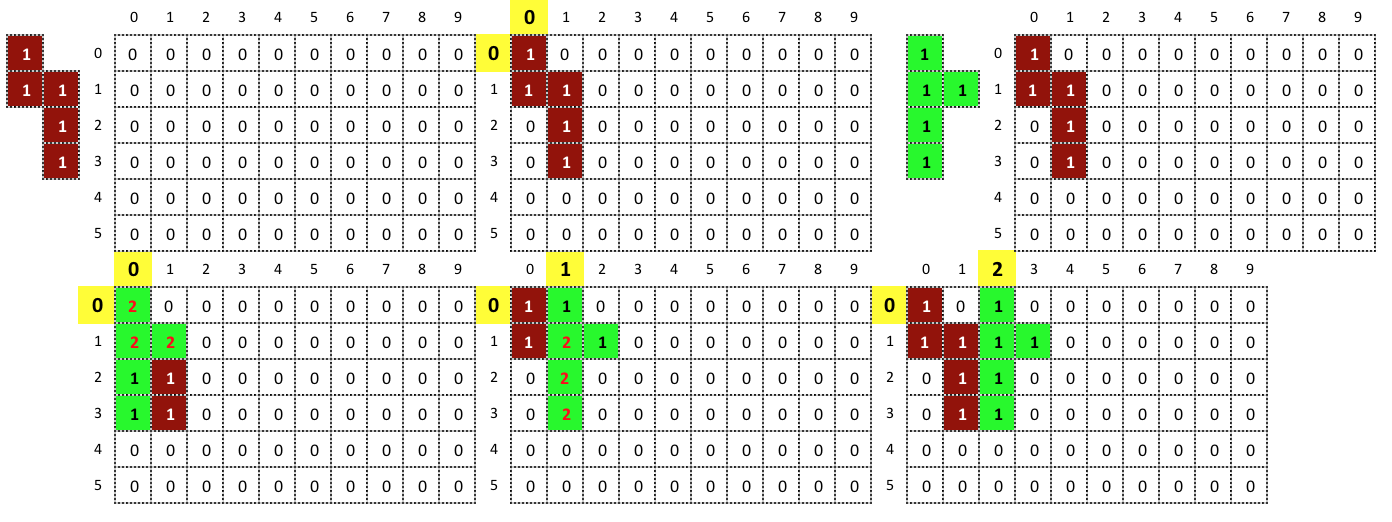
What we do here is “sliding” the pieces along the puzzle board until they “fit”.
By “sliding” I mean iterate from Top to Bottom and from Left to Right. By “fit” I mean that the sum of the values of the piece array that describes it, and the values of the cells of the puzzle board are less than 2, relative to the position of the piece on the puzzle board while is being “slid”.
For example, here you can see how the first two pieces are placed:
In a more complex scenario, placing a piece could mean testing almost the entire puzzle board for available space:
The recursive call on each combination of Pieces and Configurations is very important because this is what enables that each possible combination of Pieces and Positions within the puzzle board is tested.
Well, that’s the easiest part of the problem, just find any “empty” space within the puzzle board and, if successful, it is not solved, otherwise, You’re Lucky! You found a Solution!
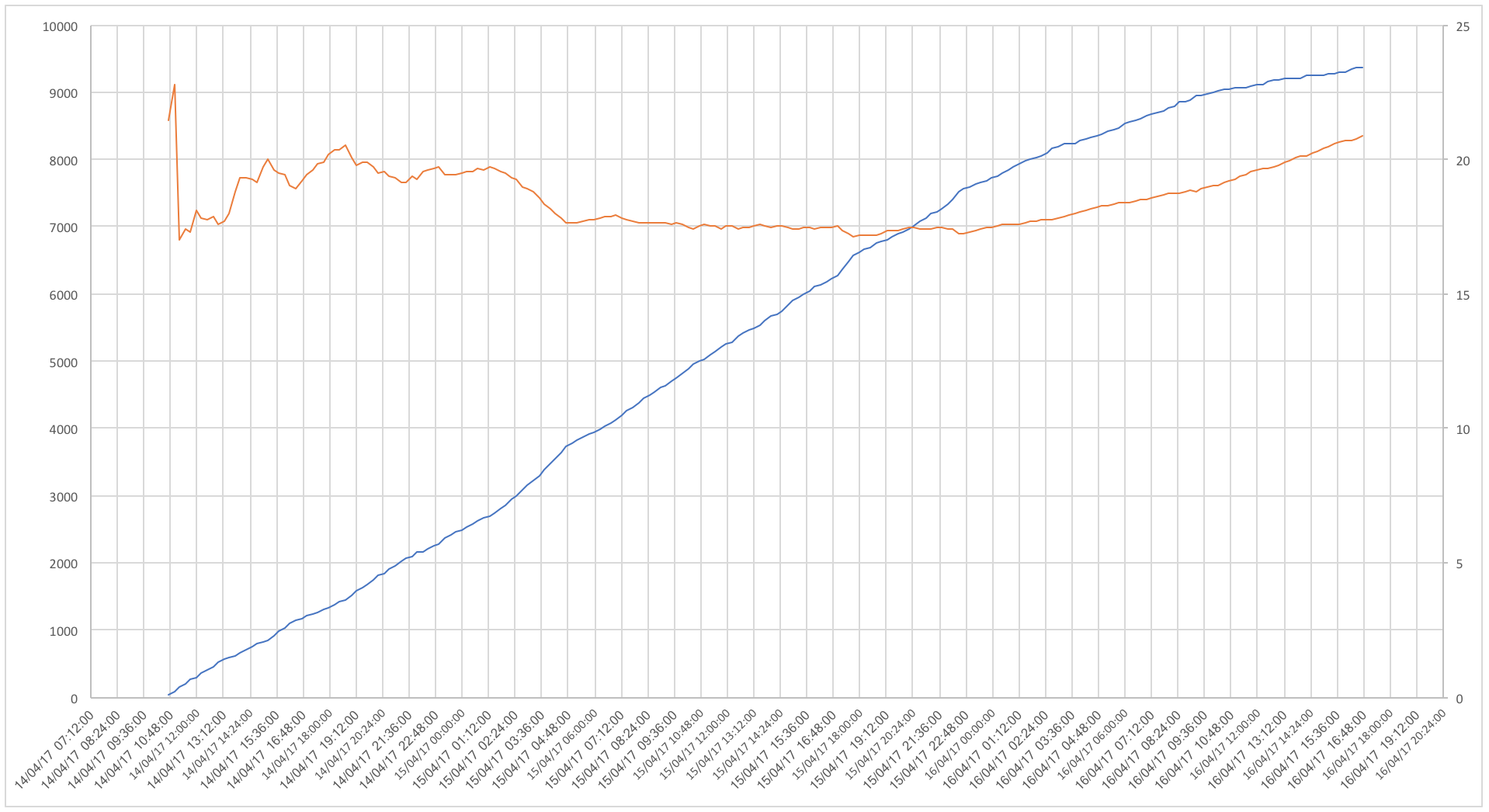
In a QuadCore CPU, 16 GB Ram, SSD, desktop computer, the version 0.0.3 (https://github.com/aaguilerav/puzzle_solver) of this software delivered the following results:
- Number of solutions found: 9356
- Number of total hours of computation: 54.25 hours
- Time on average to find a solution: 20 seconds
In the following graph, you can appreciate the number of solutions found over time (blue line) vs the average time that it took to find one solution at a given point in those 54.25 hours.
If you want to see each one of the 9356 possible solutions you can do it here: https://raw.githubusercontent.com/aaguilerav/puzzle_solver/master/src/test/resources/puzzle-solver-0.0.3.txt
There is a script named compile.sh that you can use in order to compile and package the project. Or, just execute the following command: mvn clean compile assembly:single.
The JAR file is created at puzzle_solver/target, just execute a java -jar <jar file generated>. At the beginning of the execution you'll see the following ASCII art:
+-------+---+-------+-----------+---+---+
| | | | | | |
| +---+ +---+ +---+ +---+ | |
| | | | | | |
| +-------+ +---+ | +---+ | |
| | | | | | | | | |
| | +---+---+ +---+---+ | | |
| | | | | | | |
+---+ | +---+ +---+ +---+---+ |
| | | | | | | | |
+-------+ | +---+ | | +---+
| | | | |
+-----------+-----------+---+-----------+
+---------------------------------------+
| PUZZLE SOLVER v0.0.x |
+---------------------------------------+
- Maybe using GPU processing power could give this program a big boost. Who knows, I need to try.
- A possible enhancement could be “mirroring” each solution found horizontally and vertically. This means that, in theory the time that it now takes to find all 9356 possible solutions could be slashed by a factor of 4.
Please send any comment about this article to aaguilerav@me.com, If you find a bug or a better solution to this problem please share your ideas.