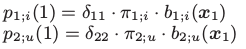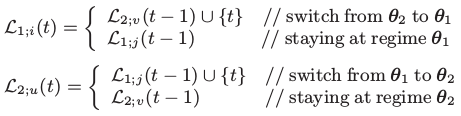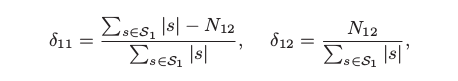AutoPlait

AutoPlait是一个NB的自动数据挖掘算法, 由Yasuko Matsubara, Yasushi Sakurai以及Christos Faloutsos三位于2014年共同在sigmod上发表的论文中提出.

它给出了如何在"共同演化"(co-evolving, 目前不知道翻译成"向前依赖"好不好)的时间序列(如动作捕捉传感器的数据, web页面上的点击, 社交网络上的用户行为)上做高效, 自动化分析的方法.

注1: 该repository是HIT-2012级软件工程-算法课的self-choice课程设计之一.
注2: 最近在做BTC时序分析+数据可视化和ctheyvs用户行为统计分析,于是挑选了这个能对该研究最有启发作用的论文(怎么说也是百里挑一的巧合~~).

abstract

给定一个包含模式不同且数量未知的海量时间序列数据集合.

如何有效并且高效的找出典型的模式和变化点?

如何从统计学角度归纳总结所有的序列,并得到一个有意义的段?

针对如上问题,该论文给出了一个算法autoplait, 具有如下特点:

• 高效
• 可扩展(时间复杂度呈线性变化)
• 参数自由
• 人类可读(分析结果便于理解)

这个算法目标是完成时间序列的CAPS(数据压缩, 异常检测, 模式提取, 分段). 即分析一个巨大的时间数据集合,并给出数据序列的最佳的表示形式.

autoplait算法可以自动区分并标识出一个时间序列中所有模式(或制式regime),并找出序列中每个模式发生变化时的位置.

其他调查:

对于时间序列的分析包括"模式提取", "总结", "分组", "分段"和"序列匹配".

但是目前针对这些分析的方法至少都需要对算法参数进行人为调整,因此对参数的依赖过于严重.除此之外,对模式的分析也不够准确和清晰.

而理想的方法应该在不涉及人指导和参与的情况下自动提取任意模式.

问题描述

在这之前, 先定义几个需要用到的变量和模型.我们将用如下数学符号来描述问题的整个解决过程.

定义

1. 设序列X为Bundle.

      X = { x1, ..., xn }
   

   X为一个长度为n的d维时序集合, xt为t时刻的d维向量.

2. 设序列中的模式为Regime.

      S = { s1, ..., sm }
   

   S为包含m个不重叠的段的集合, si由某个开始和结束时间段组成的第i个段,即si = {ts, te}.

   将每一个段分到一个段组(segment group), 从而找到相同模式的段的集合, 这个段组称为Regime. 其中每个段组由统计模型θi (i = 1, 2, ..., r)表示.r为regime的数量.

3. segment-membership

      F = { f1, ..., fm }
   

   fi (fi ∈ [1, r])是第i个段所属的regime编号.

4. 候选式

      C = { m, r, S, Θ, F }
   

5. regime模型参数 Θ = { θ1, θ2, ..., θr; ∆r×r }, ∆r×r描述见下↓.

6. Regime转换矩阵 △r×r为r阶regime的"转换概率矩阵",元素δi,j∈∆表示从第i个regime到第j个regime的转换概率.(0 ≤ δi,j ≤ 1, δi,j = 1)

Note: 这里统计模型θ由HMM模型表示

HMM模型

hidden Markov model, 包含:

• 模型状态数: k
• 初始化状态概率: π = { πi }, i = [1, k]
• 状态转换概率: A = { aij }, i,j = [1, k]
• 输出概率: B = { bi(x) }, i = [1, k]

似然函数:

对于给定模型θ, 时间序列X, 似然值P(X|θ)计算方法如下:

	P(X|θ) = max{ pi(n) }(1 ≤ i ≤ k)

其中pi(t)是t时刻状态为i的最大概率:

	pi(t) = 1. πibi(x1)		(t = 1)
    		2. max{ pj(t-1) * aji } * bi(xi)	  (2 ≤ t ≤ n)

问题: 如何全自动化CAPS?

我们可以把问题归纳为计算:

• S
• F
• Θ

这样问题就可以转化为"如何求出合适的r和m的值"(也就是"如何将时间序列分段分组").

下面给出解决问题背后的两大核心思想:

1. Multi-level chain model (MLCM): 处理多级转换的模型,如"将HMM的状态分成regime,把regime继续分级成super-regime",可以完成段的划分到regime的划分工作
2. Model description cost: 计算开销的模型, 自动估计合适的参数

计算上的时间复杂度:

序列数量n和维度d: log*(n) + log*(d) 段数m和regime数r: log*(m) + log*(r) 段分配给regime需要: mlog(r) 每个段si的长度: Σlog*(|si|) (i = 1; m - 1)

开销计算:

	CostT = Cost(M) + Cost(X|M)

Cost(M)为计算模型M的开销,Cost(X|M)为给定模型M计算数据X的开销.

regimes模型参数计算:

	CostM(Θ) = ΣCostM(θi) (i = 1; r) + CostM(∆)
    
    CostM(θ) = log*(k) + cF*(k + k^2 + 2kd)
    CostM(∆) = cF * r^2

其中cF为浮点计算开销, k + k^2 + 2kd为单个regime模型计算开销.

对于给定模型参数Θ,序列X的编码开销:

	CostC(X|Θ) = ΣCostC(X[si]|Θ) (i = 1; m)
    		   
               = Σ(-ln{δvu*(δuu)^(|si| - 1) * P(X[si]|θu)})
    
    CostC(X|Θ) = log2(1/P(X|θ)) = -ln(P(X|θ))

综上, 在时序X上总的计算开销为:

	CostT(X; C) = CostT(X; m, r, S, Θ, θ)
    = log*(n) + log*(d) + log*(m) + log*(r) + mlog(r) 
      + Σlog*(|si|) (i = 1; m - 1)
      + CostM(Θ) + CostC(X|Θ)

让我们回到这个问题的描述上, 所谓"合适的r和m", 能使上面这个开销函数最小化.

算法设计

autoplait算法的最终输出是一个最优的候选式C = { m, r, S, F, Θ }

算法分为三部分:

1. CutPointSearch: 最内部的循环, 从r=2开始. 目标是寻找合适的段切分点.(为何分段? 后面的分段比较中会谈到)
2. RegimeSplit: 中间循环, 估算合适的Θ, 也从r=2开始.
3. AutoPlait: 最外层循环, 查找最优的r, (r = 2, 3, ...)

下面这段的翻译可能不太准确 归结起来就是: 依据开销模型选择耗时最少的方法, 包括r和m的选择. 递增r,m的值, 逐渐寻找更合适的表示X的候选式, 并且在每次产生新的分段和确定regime后, 新的模型计算开销会大大减少.

算法1: (CutPointSearch)

• 输入: X, θ1, θ2, ∆2×2
• 输出: 每个分段集合(regime)和集合长度

CutPointSearch (X, θ1, θ2, ∆) {
  // 计算p1;i(t)和p2;i(t)
  for t = 1→n do
    计算状态i=1~k1的p1;i(t)
    计算状态u=1~k2的p2;u(t)
    计算状态i=1~k1的L1;i(t)
    计算状态u=1~k2的L2;u(t)
  end
  
  // 划分成两个段集合
  选择最优切点集合Lbest
  ts = 1 // 第一个段的起点
  for each 切点,li in Lbest do
    创建段si = { ts, li }
    if i是奇数
      把si添加到S1
      m1++
    else
      把si添加到S2
      m2++
    end
    ts = li
  end
  
  return { m1, m2, S1, S2 }
}

计算公式

  Θ = { θ1, θ2, ∆ },
  θ1 = { π1, A1, B1 }, k1
  θ2 = { π2, A2, B2 }, k2
 

 L = { l1, ..., lm-1 } 
 // 表示切点位置集合, 其中li(1 ≤ i ≤ n)为第i个切点.
 // 为两个regime的每个状态保存候选切点.

算法2: (RegimeSplit)

在这层循环中找出最小的建模开销:

1. 通过编码开销找出段的切点
2. 从新的段上计算Θ (使用BaumWelch推算)

• 输入: X
• 输出: m, S, θ, ∆

  初始化模型θ1, θ2
  
  while 开销↓ do
    // 执行算法1, 查找段
    {m1, m2, S1, S2} = CutPointSearch(X, θ1, θ2, ∆)
    // 更新Θ
       θ1 = BaumWelch(X[S1])
       θ2 = BaumWelch(X[S2])
    更新regime转换矩阵∆
  end
  
  return { m1, m2, S1, S2, θ1, θ2, ∆ }

过程解释:

模型初始化

从X中均匀的选择一些段, 对于每个子序列, 得到模型θs. 从而得到所有可能的{ θs1, θs2 }, 并从中选取最合适的{ θ1, θ2 }.

{ θ1, θ2 } = min CostC(X|θ1, θ2)

模型估计

关于HMM上的k的计算.
如果k过小, 则模型对数据的贴近程度很弱, 并且算法可能找不出优化的段. 同样的, 如果k过大, 则模型的表达能力变弱("过渡适配").

转换矩阵元素的计算

Σ|s| s∈S1是属于regime θ1的段的总长度.
N12是从θ1-θ2, regime转换的次数.

算法3: (AutoPlait)

完成任务: 自动化无需用户干涉, 切点定位准确, 能区分不同模式.

前面研究的是对于m, r=2的情况,找到段和切点. 那么如何确定段数为m以及regime的数值r?

第三个算法是一个基于栈的算法, 思想是使用贪心算法, 将一个X分成段, 并引入新的regimes(只要编码开销一直↓)

• 输入: X
• 输出: 对Bundle X的一个描述C

  Q = ∅  // { m, S, θ }的栈
  S = ∅, m = 0, r = 0, S0 = { 1, n }, m0 = 1
    θ0 = BaumWelch(X[S0]) // 估算S0的模型θ0
  将{ m0, S0, θ0 }压入Q
  
  while 栈Q != ∅ do
    将{ m0, S0, θ0 }弹出Q
    // 尝试提取regime
    { m1, m2, S1, S2, θ1, θ2, ∆ } = RegimeSplit(X[S0])
    // 比较单一的regime θ0和regime 序对θ1, θ2
    if CostT(X; S0, θ0) > CostT(X; S1, S2, θ1, θ2) then
      // 分割regime
      把两个entry {m1, S1, θ1}和{m2, S2, θ2}压入Q
    else
      // 无需分割regime
      S = S ∪ S0
        Θ = Θ ∪ θ0
      r++
      更新∆r×r
      fi = r
      m = m + m0
    end
  end
  
  return C = { m, r, S, Θ, F }

时间复杂度为O(n)线性增长

CutPointSearch和RegimeSplit需要O(ndk^2)时间来计算编码开销和估计模型参数. 因此复杂度为O(#iterate * ndk^2), 因为#iterate, d, k很小, 因此可以忽略不计, 复杂度为O(n).