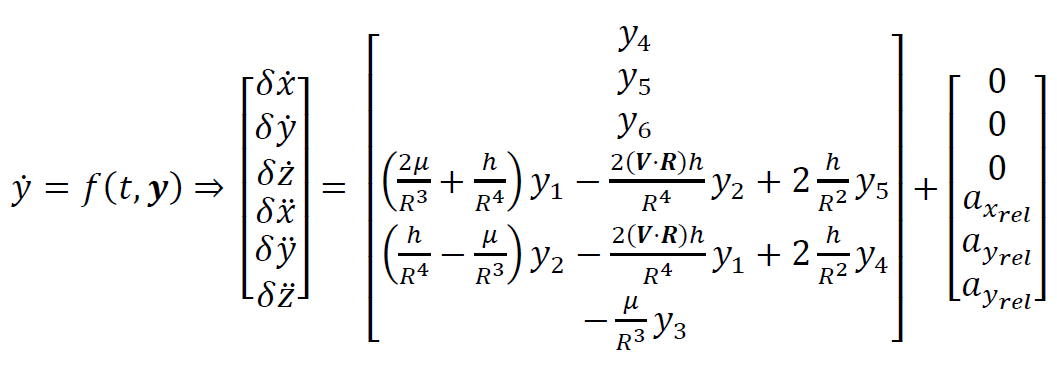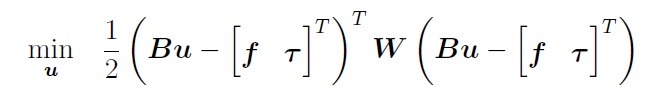This repository contains code for simulation and control of a SPHERES satellite in formation with another satellite, using a vectorized Dynamic Programming approach. Made available publicly, mainly to reproduce the work of a article that is currently in progress. Only works with MATLAB version 2016b and above. If you can't find the codes listed below you should switch to the .
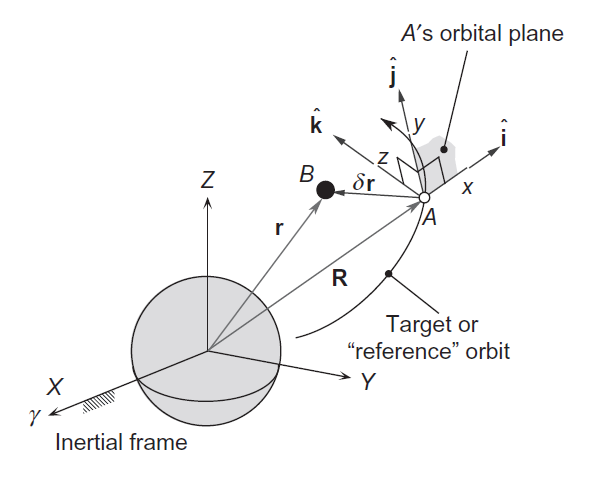
Starting from the initial conditions at t = 0, the simulator runs every 5 milliseconds and computes new state and control vectors. In each instance, the Clohessy-Wiltshire equations of relative motion are used to update the position of a target satellite A and to determine the relative position of the SPHERES satellite B that is following satellite A (in RSW frame of reference - see figure above from Curtis). The Euler's rotation equations are used as well, to update quaternions and angular velocities of the SPHERES satellite (in Body frame). The equations of position and attitude are inevitably coupled because some state variables are shared in both. The CW equations of relative motion are not simplified for circular orbits, so the complete equations are as follows:
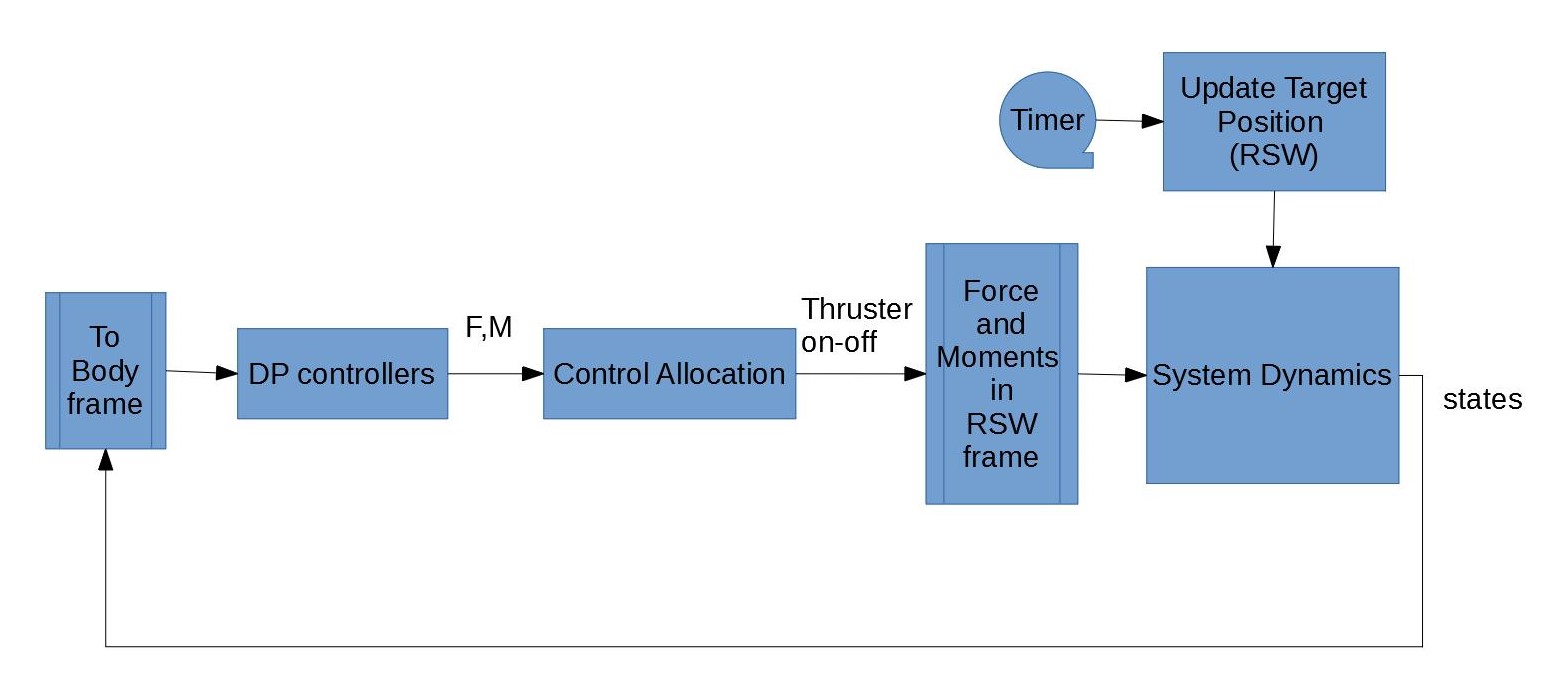
Dynamic Programming is used to generate controllers (will be explained in detail in later sections), these controllers are preloaded into the satellite, and help determine the optimal forces and moments that the SPHERES satellite requires to reach the target satellite. These required forces and moments are then converted to thruster on-off commands, using a control allocation method (will be explained in detail) such as a Pulse-Width Pulse-Frequency (PWPF) Modulator, a Schmitt trigger or the Active Set Method. After the command for all 12 thrusters are determined, the simulator recalculates all forces and moments in their respective frames, and continues the simulation to calculate the next states from the previous states and actions. Differential equations are solved using the fourth-order Runge-Kutta method (since the time steps are in order of milliseconds, there is no difference in the results of RK4 and ODE45, however, RK4 is significantly faster). The overall process of the simulation is shown in the figure below:
You can simply run the scripts to see the results. In addition, you may change the controller configurations and/or initial conditions to see how the satellite controls itself under different conditions. The script below is set with initial conditions of -0.6 meters offset in x, y, and z directions and 10 degree offset in angles. Control allocation method is set to "Active Set", additional information can be read inside the script:
%%% for Dynamic Programming Control
closedist_normal_activeset_allocation
If you want to see control with Proportional-Differential controllers in the same condition, run the script below:
closedist_normal_PD_controller_activeset
- Note: PD means Proportional-Differential, not to be confused with DP (Dynamic Programming), see inside each script for initial conditions and configurations.
The control allocation methods determine on/offs for each thruster in order to reach the nearest torques and forces in 3DOF generated by Dynamic Programming or PD controller. In other words, the forces and torques that are required to control the satellite are converted to thruster firings by the control allocation systems. There are several allocation methods defined in the simulator, one of which is Quadratic Programming:
Quadratic Programming allocation is the problem of finding the set of thruster firings (on/offs) that minimize the following quadratic cost function (from here).
The Active Set Method is not used here. Additionally, the numerical algorithms explained in some references seem quite complex to find the multi-variable answer to this problem, especially when a continuous range of values and many variables are involved. However, since SPHERES is an all-thruster satellite and the thrusters can only produce a fixed amount of force, finding the solution in this particular case is super easy. First, using the all_feasible_thruster_u function, all the possible combinations of thruster on/offs are generated for each channel of 4 thrusters. Next, each combination is put directly as u in the above cost function, and the minimum set is easily found by using MATLAB's min function and extracting the id of the set.
In each channel, when all 4 thrusters are operational, 16 (=2^4) total combinations of thruster firings are present. However, not all combinations are efficient in terms of fuel consumption. In other words, some combinations produce the same amount of forces and torques, but one of them uses less fuel in the process. This happens particularly when two thrusters in the opposite directions fire and cancel out each other. For instance, consider the case where all four thrusters fire in one channel, they all cancel each other out and produce zero force and torque in their directions, which is the same as the more fuel efficient set of all thrusters being off. Crossing out these cases not only results in more fuel efficiency but also makes the computations very efficient, too.
Additionally, this allocation method supports the scenario of faulty thruster(s). If the IDs of the faulty thrusters are determined, the combinations are automatically reduced to those in which the faulty thrusters are always "off".
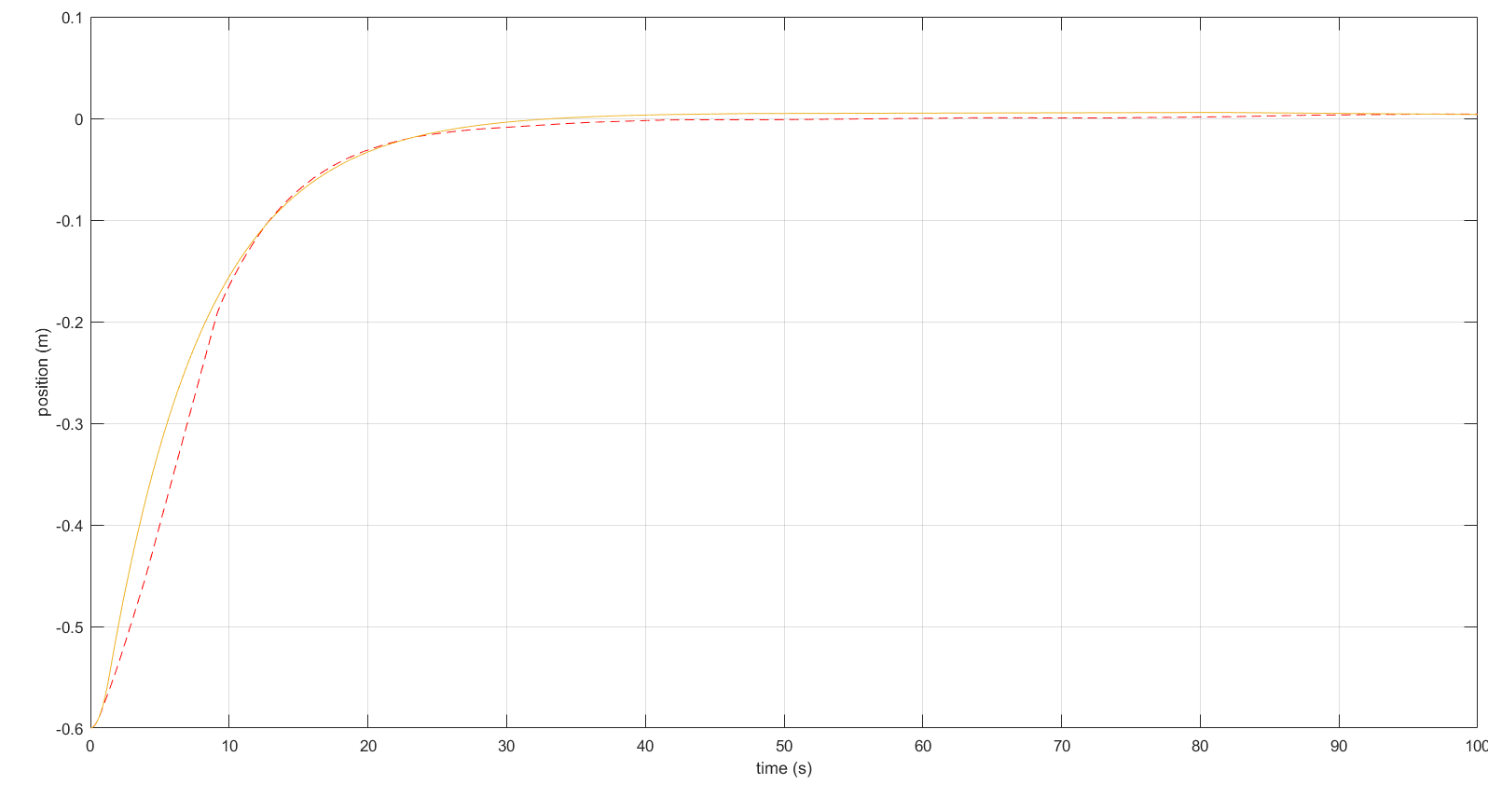
After you run the scripts, you can see how states have changed and actions taken during the entire simulation. For the example above, fuel consumption using Dynamic Programming is 23% less than PD control in only 0.6 meters of displacement. The Kp and Kd parameters for the PD controller are chosen so that both trajectories have similar settling times. The position plots in z-direction are as follows:
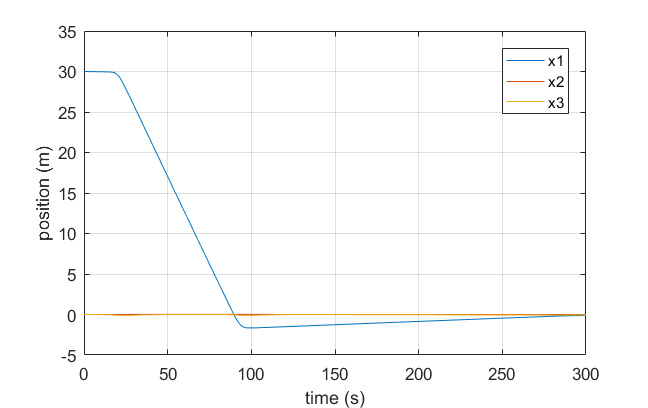
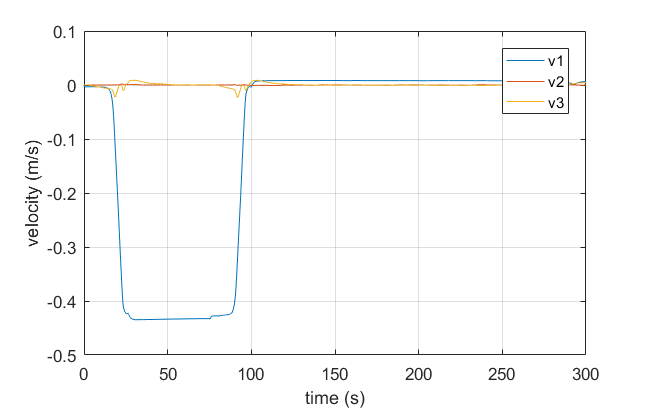
An example of how the satellite is controlled under thruster failures is shown here. The faulty thrusters are both in x-direction and back to back (thrusters #0 and #6), such that the satellite cannot relocate in x-direction without getting rotational speeds. The control allocation scheme is PWPF, and the initial offset is 30 in x-direction only. What happens in here is that the satellite performs two maneuvers, first to gain some velocity and then to lower it's kinetic energy when it has reached it's destination.
| Position | Velocity |
|---|---|
 |
 |
| Quaternions | Angular Velocities |
|---|---|
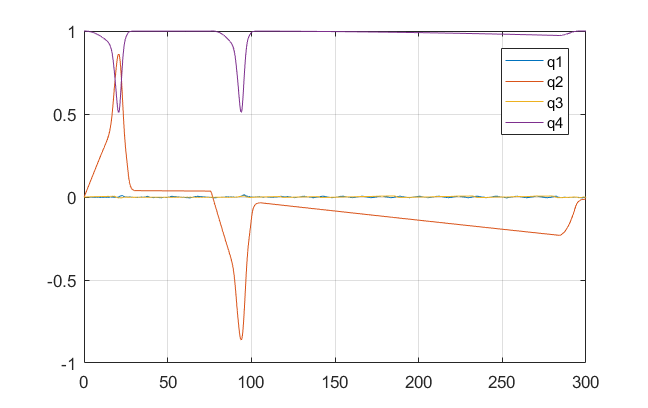 |
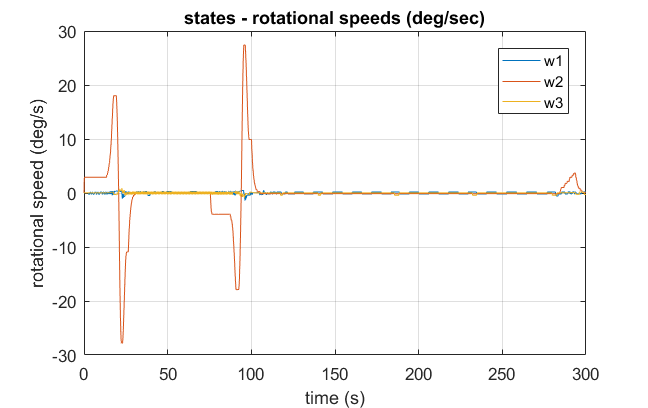 |
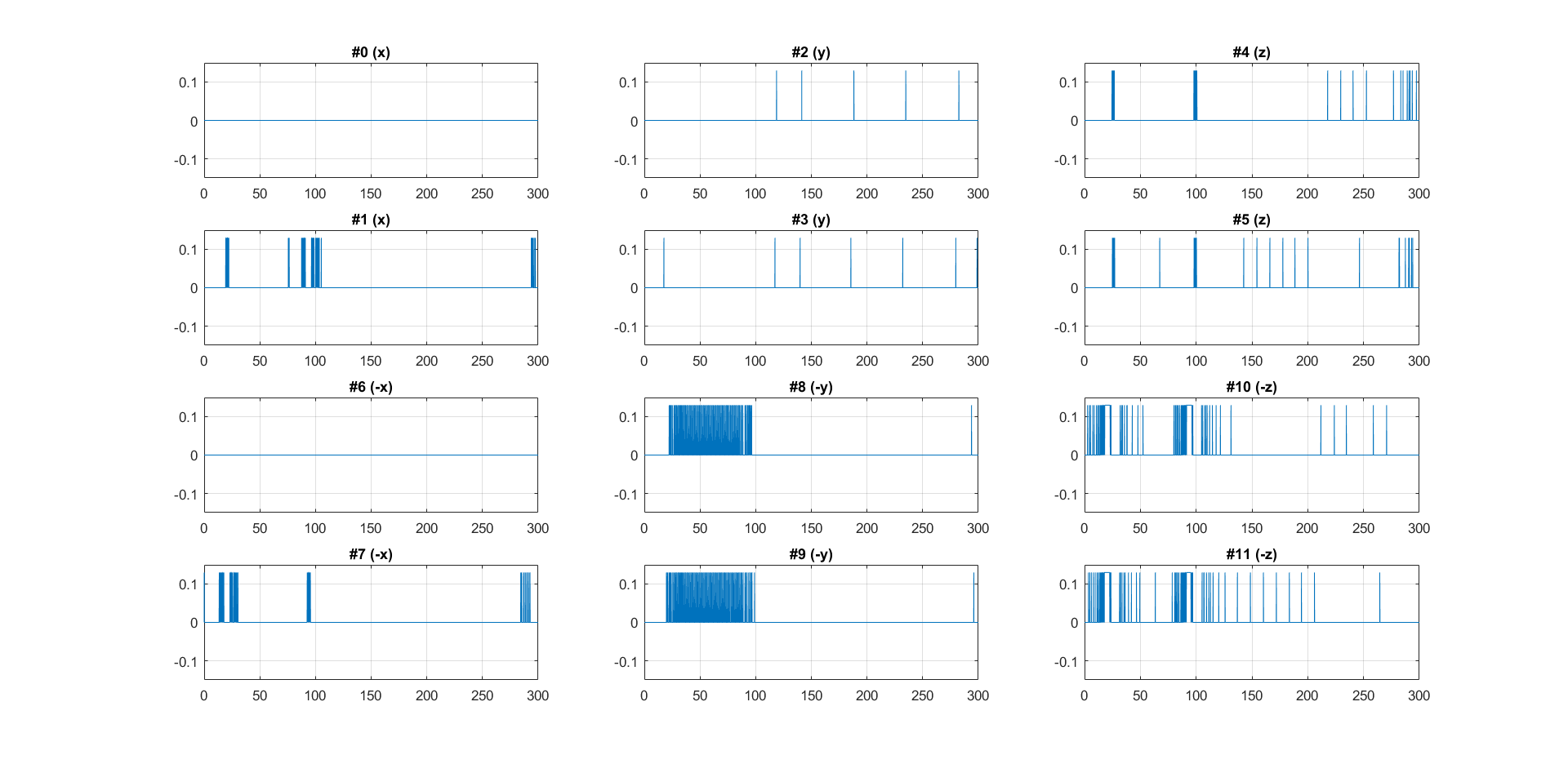
How the thrusters reacted in the above scenario is shown in figure below (thrusters #0 and #6 are faulty and therefore always off):
These figures show something amazing: the satellite can't go straight in the x-direction without gaining torque, so it rotates itself and uses the thrusters in the other directions (now with a component in the x-direction) to gain speed. Once it gains some velocity, it continues its way to reach the approximate destination and then performs the same maneuver in reverse to stop! These maneuvers were not in any way hard-coded into the simulator, so the emergence of such solution is astonishing.
This code wouldn't have been possible without exceptional support and guidance provided by Dr. Nima Assadian of the Aerospace Engineering Department at Sharif University of Technology, who was the supervisor of the project.
This project is licensed under the MIT License - Authors: Abdolreza Taheri & Dr. Nima Assadian