Tech Talks

Part 1: Public Key Cryptography

Part 1: Public Key Cryptography

• One-way functions
• Elliptic curves
• Discrete Logarithm Problem
• Schnorr digital signature algorithm
• Integrated Encryption Scheme (IES)

---

Applications of Public Key Cryptography

---

Applications of Public Key Cryptography

---

Symmetric encryption/decryption

• Block ciphers based on substitution-permutation networks
• Secure and much more efficient that asymmetric methods
• No clever maths required
• Used extensively (e.g. AES) in hybrid cryptosystems
• Requires secure key sharing

Image from https://sectigo.com/resource-library/why-automotive-key-fob-encryption-hacks-are-making-headlines

---

One-way functions

Image from An Introduction to Mathematical Cryptography by Hoffstein, Pipher, Silverman (2008)

Examples:

• Cryptographic hash functions (no trapdoor)
• Prime factorisation: $f(p, q) = p \times q , (\mbox{mod} , N)$
• Elliptic curves: $f(k) = k , G$

---

Cryptographic hash functions

> echo -n 'Bitcoin rules!' | shasum -a 256
8109fafb32577c80ab59fa77dbea41d7bcb9bc4dc4bcf22c8b635b5ad7119c3e
> echo -n 'Bitcoin rulez!' | shasum -a 256
df4b574acf74ead4a783f7b8282a087d7b14b68c92e2e1541b6fa3c0d130b7dc

• Repetitive bitwise mixing and rotation operations

• Resulting in a deterministic one-way function

• No security proofs: reliance on "diffusion and confusion properties"

• Random Oracle model: uniform draws from ${0, 1, ..., 2^{256} - 1}$

---

Aside: Modular arithmetic

$$ 5 + 9 \equiv 2 , (\mbox{mod} , 12) $$

$$ 5 - 7 \equiv 10 , (\mbox{mod} , 12) $$

$$ 9 \times 6 \equiv 6 , (\mbox{mod} , 12) $$

$$ 3 , / , 7 \equiv 9 , (\mbox{mod} , 12) $$

Or rather $3 \times 7^{-1} \equiv 3 \times 7 , (\mbox{mod} , 12) \equiv 9 , (\mbox{mod} , 12)$

Note that $6^{-1}$ does not exist (as 6 is not coprime to 12).

---

The story so far...

• We want to be able to encrypt/decrypt and create signatures
• Symmetric encryption is easy, but how to share the key?
• We need one-way functions with some structure

---

Elliptic Curves

$y^2 = x^3 + ax + b$

Over the field of real numbers

Images from https://blog.cloudflare.com/a-relatively-easy-to-understand-primer-on-elliptic-curve-cryptography/

---

Elliptic Curves

$y^2 = x^3 + ax + b$

Point "addition": $A \cdot B = C$

Images from https://blog.cloudflare.com/a-relatively-easy-to-understand-primer-on-elliptic-curve-cryptography/

---

Elliptic Curves

$y^2 = x^3 + ax + b$

Over the finite field $\mathbb{F}_p = {0, 1, ..., p-1 }$, where arithmetic is modulo $p$

Images from https://blog.cloudflare.com/a-relatively-easy-to-understand-primer-on-elliptic-curve-cryptography/

---

Elliptic Curves

$y^2 = x^3 + ax + b$

Point "addition" still works: $A \cdot B = C$

Images from https://blog.cloudflare.com/a-relatively-easy-to-understand-primer-on-elliptic-curve-cryptography/

---

Cyclic Group Construction

Point addition is associative: $(A \cdot B) \cdot C = A \cdot (B \cdot C)$

Add a "point at infinity" $I$ intersecting any vertical line

Pick a curve point $G$

Define scalar "multiplication" $k , G = G \cdot G \cdots G$ ($k$ times), for $k \in \mathbb{F}_p$.

Consider the set of points $\mathcal{G} = {n , G$ | $n \in \mathbb{F}_p }$

This is a cyclic group generated by $G$ with identity element $I$

---

Example: curve secp256k1

Defined in http://www.secg.org/sec2-v2.pdf

$a = 0, ; b = 7$

$y^2 = x^3 + 7$

$p = 2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1$

Finite field $\mathbb{F}_p = { 0, 1, ..., p - 1 }$

G = 02 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798

Generates cyclic group $\mathcal{G} = { n , G , | , n \in \mathbb{F}_p }$

In this case the curve has a prime number of points

By Lagrange's Theorem, the subgroup $\mathcal{G}$ has the same order:

|G| = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141

---

Discrete Logarithm Problem

What was the point again?

For cryptography, we need a one-way function

Scalar multiplication on the cyclic group $\mathcal{G}$ is ideal:

Given the point $k , G$, there is no known algorithm to find $k$ (except brute force)

We could regard $G \cdot G \cdots G$ as $G^k$ (rather than $k , G$), hence discrete logarithm.

---

Digital Signatures

H/t https://popeller.io/schnorr-basics

Ingredients:

private key	$k$
public key	$K = k , G$
message	$m$
random nonce	$r$
nonce commitment	$R = r , G$

• Lowercase $\Rightarrow$ scalar (in the finite field)
• Uppercase $\Rightarrow$ curve point

---

Schnorr Signature algorithm

H/t https://popeller.io/schnorr-basics

Signer:

• Computes the challenge hash: $h = H(m || R)$
• Computes $s = r + h , k$
• The signature is the pair $(s, R)$

Verifier:

• Knows the public key, message & signature
• Computes the challenge hash $h$
• Checks that $s , G = R + h , K$

Conclusion: either the signer knows $k$ and $r$, or they solved the DLP!

---

Schnorr Signature algorithm

H/t https://popeller.io/schnorr-basics

• Why do we need the (secret) random number $r$?

Otherwise the signature equation $s = r + h , k$ could be solved for the secret $k$

• Why must $r$ only be used once (with any given $k$)?

Otherwise we'd have two equations & two unknowns: $s = r + h , k$ $s^\prime = r + h^\prime k$

• Why is $R$ in the challenge hash?

If instead $h = H(m)$, we could pick any $s$ and compute $R = s , G - h , K$ to get a valid signature $(s, R)$

---

Integrated Encryption Scheme (IES)

Hybrid encryption scheme:

• convenience of public key cryptography
• efficiency of symmetric key encryption

Secret key sharing is easy:

• Alice has private key $a$ and public key $A = a , G$
• Bob has private key $b$ and public key $B = b , G$
• They have the private (session) key: $$a , B = a , (b , G) = b , (a , G) = b , A$$

---

Part 2: Web Public Key Infrastructure

Recap: encryption/decryption

Allows messages to be passed between Alice and Bob privately without E(a)ve(sdropping)

---

Recap: digital signatures

Allows messages to be passed between Alice and Bob without tampering by Eve

---

Recap: hash functions

Allows messages of any length to be cryptographically compressed into digests that have tiny probabilities of being manufactured with other data

---

Problem setting

• Given we have digital signatures and encryption, how can entities who have not met trustfully communicate over channels using these tools?

---

Web Public Key Infrastructure

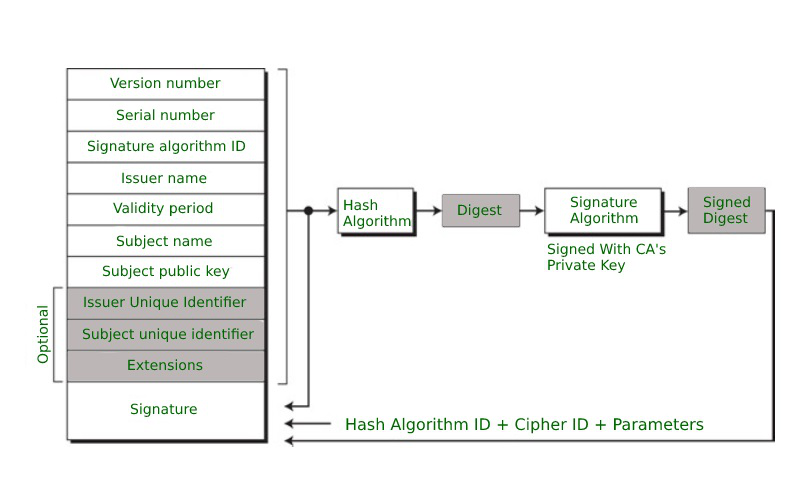
• Web Public Key Infrastructure is one way to bind of identity to cryptographic keys

• It uses a combination of hashing and digital signatures of public keys to produce digitial certificates with the third party vouching for the key

---

Who makes the certificates

• Certificate Authorities (CAs) are responsible for signing keys to certify identity, there are many hundreds of them

• Some major ones: DigiCert, Globalsign, Let’s Encrypt, Amazon, Google, ...

• Their certificates are ready installed in your browser (there are well over 100 in Mozilla Firefox/Chrome/etc). Therefore your browser maker (e.g. Mozilla, Google, Apple, Microsoft, etc) assumes this trust for you

---

How do certificate authorities check identity

• Three different degrees of checking:

  • Domain validation: checking the key owner controls the domain they claim

  • Organization validation: they check with third-party records and sources the organization is legitimate

  • Extended validation: they spend even longer doing the organization check

• There's no field on a certificate saying which of these were performed

---

What do certificates look like: Certificate standard X.509

Image from: https://www.geeksforgeeks.org/x-509-authentication-service/

---

Certificate chains

Image from: https://knowledge.digicert.com/solution/SO16297.html

---

The certificate chain securing this talk!

• Click on the 🔒 in your browser address bar and View Certificate

---

(Recent) secure network protocols

Image from: https://en.wikipedia.org/wiki/Transport_Layer_Security

• TLS is the most widely used secure network protocol using this model

• Ancestors date back to the 1980s through various incarnations

• Updates to protocols over time have been in response to weaknesses, but general process remains similar

• E.g. POODLE ("Padding Oracle On Downgraded Legacy Encryption") vulnerability affecting SSL 3.0

---

Concrete example: TLS with a customer, bank and certificate authority

• A customer of a bank wants to go to it's website access their account securely.

• How does it exactly work?

Image from: https://www.f5.com/content/dam/f5-labs-v2/article/articles/edu/20210715_what_is_mtls/digital_certificate_trust_for_tls_https.png

---

TLS: validating

---

TLS: exchanging data (symmetric key)

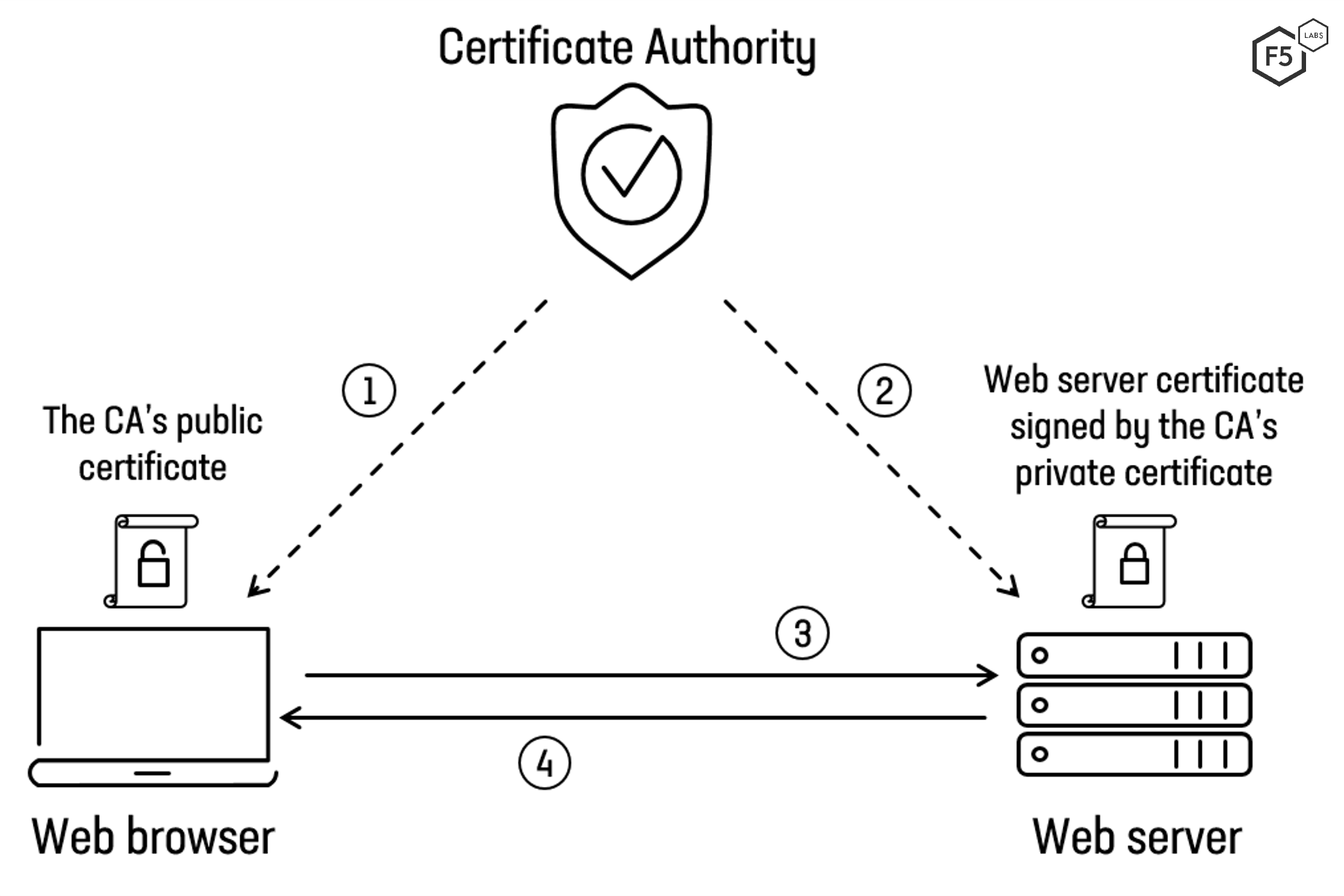
• An example of emphemeral Diffie-Hellman

---

Problems with Web PKI

• Some specific problems were highlighted by "the Internet Architecture Board" in 2016:

  • Weak Cryptographic/Short Public Keys

  • Certificate Status Checking

  • Lack of automation for Server Administrators

  • Surprising Certificates (relates to "man-in-the-middle" attacks)

---

Weak Cryptographic Keys, Status Checking and Automation

• Many short keys exist in CAs (e.g. 1024-bit RSA and SHA-1, back in 2016)

• Continuous problem as cryptographic keys get weaker over time with improved analysis methods

• No guarantees of updates being made when they are needed and were often found to be not

---

Certificate Status Checking

• Boils down to checking whether a certificate is currently valid

• No guarantees of when/if your browser will do this

---

Lack of automation for Server Administrators

• Arduous process of engagement with certificate authority means system admin do not always have the resource to do this

• Attempts at interoperable automation have not been successful in the past

---

Surprising Certificates (relates to "man-in-the-middle" attacks)

• An issued certificate exists for a subject (e.g. a bank) that was not requested by the bank

• The issue for the user - how can they distinguish the two certificates from CAs they trust with different keys?

• Verifiable timestamping can help with recent optional extensions with Signature Certificate Timestamp (SCT) fields

• However, if only one is available and it is a spurious one, the client will proceed to trust it

---

Example "man-in-the-middle" attack (see surprise certificates)

• Key point: Trust is placed in certificate authorities to correctly associate keys with entities real identity and there is no enforced hierarchy of trust among multiple certificates

---

Summary: Certificate authorities as a Centralized Trust Infrastructure

• Certificate authorities are a centralized trust infrastructure

• Trust is placed by in them to correctly vouch for identity

• The model is flawed due to its centralization; a point of failure lies within a third party

• It relies on CAs being infallible (but they are...)

---

Interlude: Trustchain solves!

• Trustchain aims to solve some of these problems with its key infrastructure (though not be replacing the Web PKI!):

  • No third party CAs as decentralized

  • Streamlined processes of revocation and rotation

  • Accessible and verfiable timestamped data (IPFS and Bitcoin)

  • Open software

  • Automation in reference client

But more on this next time!

---

Web Public Key Infrastructure: when it goes wrong!

Example: KLAYswap

On Thursday, February 3, 2022, attackers stole ~$1.9 Mio. from users of the Korean cryptocurrency exchange KLAYswap. The attack did not target KLAYswap itself, but exploited the trust that the WebPKI places in the internet routing infrastructure.

---

What happened?

Attackers didn't target KLAYswap directly, but the instant messaging platform **KakaoTalk**.

Image from: https://freedom-to-tinker.com/2022/03/09/attackers-exploit-fundamental-flaw-in-the-webs-security-to-steal-2-million-in-cryptocurrency/

---

What happened?

The attackers used a Border Gateway Protocol (BGP) hijack.

Image from: https://freedom-to-tinker.com/2022/03/09/attackers-exploit-fundamental-flaw-in-the-webs-security-to-steal-2-million-in-cryptocurrency/

---

Border Gateway Protocol

The internet is a network of network, with tens of thousands autonomous systems (AS), each of which controls a block of IP addresses.

The BGP is responsible for directing data packets on the fastest route to their destination.

---

BGP hijack

---

BGP hijack to obtain certificate

Image from: https://freedom-to-tinker.com/2022/03/09/attackers-exploit-fundamental-flaw-in-the-webs-security-to-steal-2-million-in-cryptocurrency/

---

Questions

---

Part 3: Trustchain