最近尝试了一个数据比赛，截止2021年2月，成绩是 rank 7 / 4313

@[toc]

1. 特征工程

1.1 特征工程总览

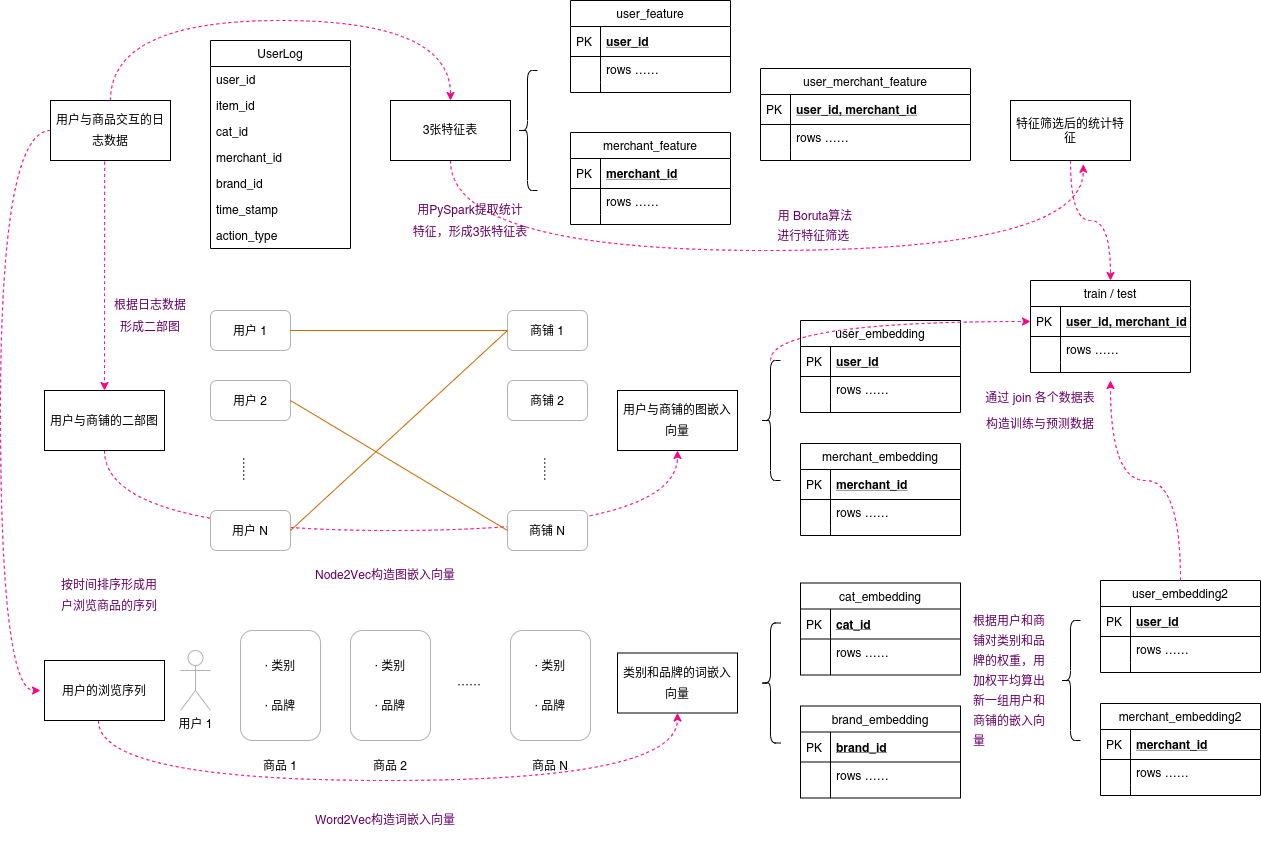
图1. 本项目特征工程总览

上图为本项目用到的特征工程，主要分为统计特征，图嵌入特征，词嵌入特征，最后通过join操作将各个特征join到主键为user_id, merchant_id的训练数据上。

如果您觉得图片过于模糊，可前往 Github 下载PDF。

1.2 通过PySpark构造统计特征

• 特征构造器：build_feat_pyspark.py
• 调用特征构造器：fesys_pyspark.py

1.2.1 特征构造器的特点

本项目的一大创新点就是开发了一个 特征构造器 FeatureBuilder 。该构造器专门用于构造日志数据中的统计特征，其特点有：

1. 以主键为核心构建特征表
2. 支持通过where语句来丰富特征库
3. 支持dummy计数、用户自定义聚集函数等操作获取统计特征
4. 采用PySpark计算，可在集群中并行

该构造器的设计哲学是以主键为核心构建与主键相关的特征列。如本赛题中，训练数据的主键为user_id, merchant_id，那么我们就可以构造出user_id, merchant_id, user_id, merchant_id 这三个特征表。

例如，在user_id特征表中构造用户最喜欢的商品、店铺等统计特征，在merchant_id特征表中构造商铺历史中各个年龄阶段的占比等统计特征，在user_id, merchant_id特征表中构造用户，商铺的交互次数等统计特征。

同时，我们还可以通过加上where语句让特征成倍地增加。例如，除了计算全局的（即不加where的）统计特征外，还可以计算双十一期间的统计特征，有购买行为限定的统计特征等等。

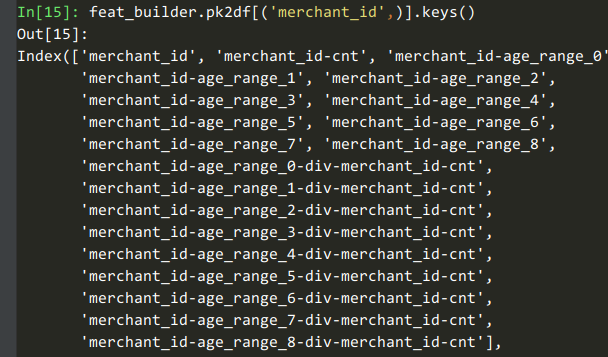
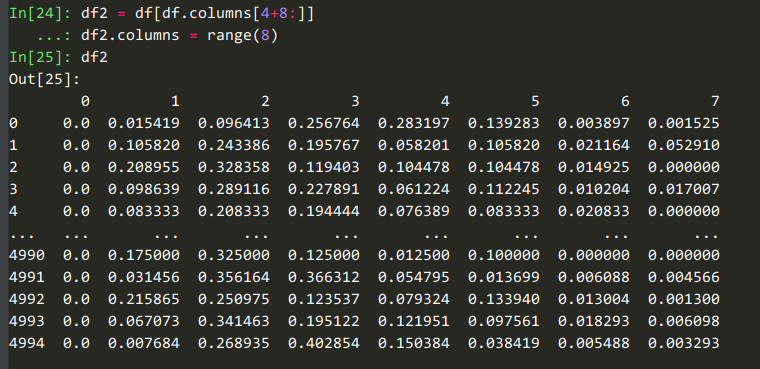
我们用一个例子讲讲dummy计数、用户自定义聚集函数这些特性。例如我们获取【商铺在各个年龄段的计数和占比】这些特征时，可以用这个代码：

feat_builder.buildCountFeatures('merchant_id', ['age_range'], dummy=True, ratio=True)
# agg_funcs=['mean', 'max', 'min', 'median', 'std', 'var', unique_udf]

可以看到这8列是对【商铺在8个年龄段的计数】的统计。

这8列是对【商铺在8个年龄段的占比】的统计。

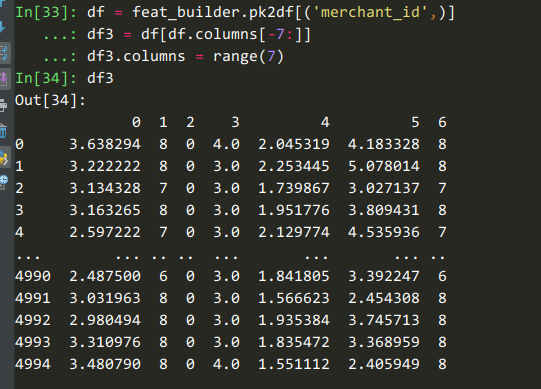
如果我们要获取【商铺购买记录中年龄段的最小值、最大值、平均值等统计量】这些特征时，可以用这个代码：

feat_builder.buildCountFeatures('merchant_id', ['age_range'], dummy=False, ratio=False,
agg_funcs=['mean', 'max', 'min', 'median', 'std', 'var', unique_udf] )

最后，特征构造器 支持持久化序列化等操作，在构建训练数据与测试数据时只需要依次将各个特征表join到主表即可，使各个特征解耦和。

1.2.2 可以构造哪些统计特征

• 计算用户和商铺的复购次数（复购率用rebuy_udf算）
• 【商家】与用户的【年龄，性别】两个特征的交互
• 【商家，商品，品牌，类别】与多少【用户】交互过
• 【用户】与多少【商家，商品，品牌，类别】交互过（去重）
• ※ 【商家】,【用户，商品】与多少【商品，品牌，类别】交互过（去重）
• ※【用户，商家，商品，品牌，类别】的【action_type】统计 （行为比例）
• 【用户，商家，【用户，商家】】每个【月，星期】的互动次数, 持续时间跨度，用户与商铺开始、终止时间统计
• “最喜欢”特征，如用户最喜欢的商家、商品，主宾都可以互换
• ※ 用户在商铺的出现比例, 以及相反
• ※ 用户和商铺的复购率
• 对各种频率分布进行统计。如：商铺的用户序列是 [user1, user1, user2], 那么频率分布就是[2,1]，计算这个分布的统计特征，如方差。

然后，取action_type=purchase的where条件，再把上述特征计算一遍。

最后，取交互日期为双十一的where条件，把上述星号※的特征计算一遍。

1.3 通过Node2Vec构造图嵌入特征

• 生成二部图数据： create_graph_embedding_data.py
• 训练Node2Vec： train_node2vec.py

1.3.1 为什么用graph-embedding获取隐向量

为什么要用对二部图做graph-embedding的方法获取用户和商铺的向量呢？

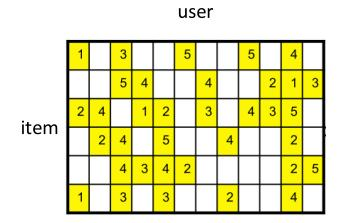
我们知道，在推荐系统中有一个user-item共现矩阵，如下图：

图2. user-item共现矩阵

如果我们要通过user-item共现矩阵得到user-embedding和item-embedding，一般有两种做法：

1. 对这个矩阵进行矩阵分解，如SVD或神经网络的方法，得到隐向量。
2. 将矩阵视为词袋，用TF-IDF再加上LSA、LDA等方法得到主题向量。
3. 按照时间顺序整理用户看过的物品序列，用Word2Vec学习这个序列中上下文的相关性，得到物品隐向量。反之得到用户隐向量。
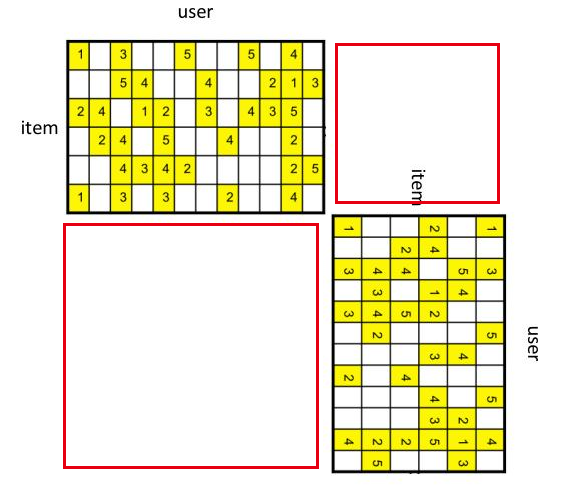
4. 将user-item共现矩阵转换为二部图的邻接矩阵（图3）后，可以在这个图上使用deep-walk，node2vec等graph-embedding的方法得到图嵌入向量。

· 图3. user-item二部图邻接矩阵

本项目经过综合考虑，选择了方案4，即图嵌入的方案，理由如下：

1. graph-embedding得到的用户向量与店铺向量之间的内积可以表示用户对商铺的喜欢程度，与矩阵分解的性质相似。方案2和方案3没有这个性质。
2. graph-embedding可以考虑到一些隐含信息，如用户1和用户2都喜欢店铺A，而用户1还喜欢店铺B，这样用户2也有可能喜欢店铺B。这样的隐含信息是矩阵分解学不到的。

1.3.2 什么是Node2Vec

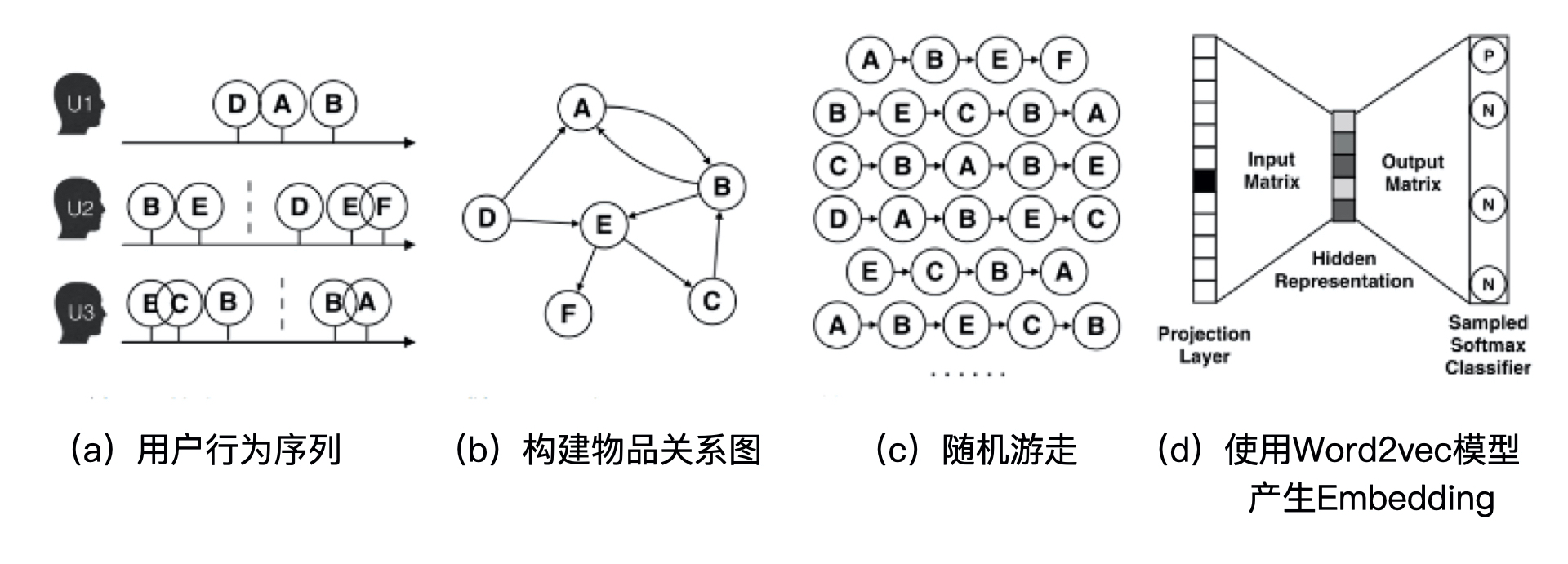
图嵌入算法中最常见的是Deep Walk，它的主要思想是在由物品组成的图结构上进行随机游走，产生大量物品序列，然后将这些物品序列作为训练样本输入 Word2vec 进行训练，最终得到物品的 Embedding。因此，DeepWalk 可以被看作连接序列 Embedding 和 Graph Embedding 的一种过渡方法。图 4 展示了 DeepWalk 方法的执行过程。

图4 DeepWalk方法的过程

Node2Vec在DeepWalk的基础上，通过调整游走权重的方法试Graph Embedding的结果更倾向与体现网络的同质性（homophily）或结构性（structural equivalence）。其中“同质性”指的是距离相近节点的 Embedding 应该尽量近似，“结构性”指的是结构上相似的节点的 Embedding 应该尽量接近。

图5 网络的BFS和 DFS示意图

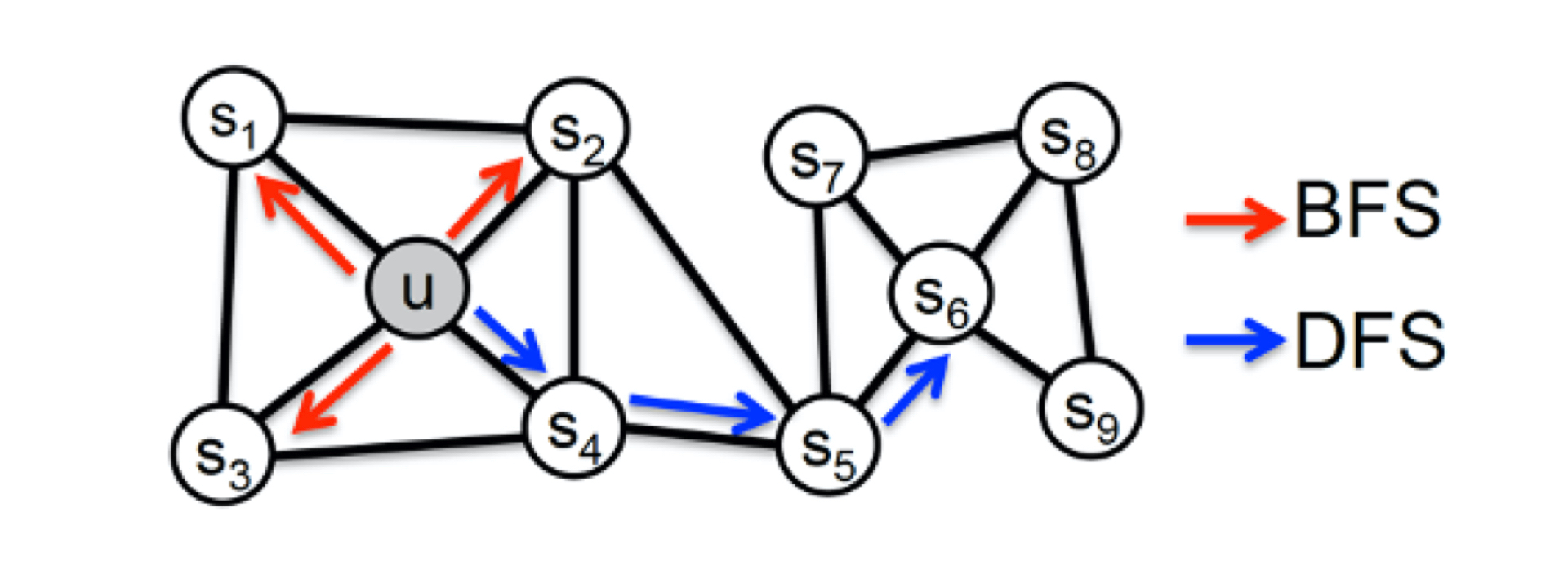
为了使 Graph Embedding 的结果能够表达网络的“结构性”，在随机游走的过程中，我们需要让游走的过程更倾向于 BFS（Breadth First Search，宽度优先搜索），因为 BFS 会更多地在当前节点的邻域中进行游走遍历，相当于对当前节点周边的网络结构进行一次“微观扫描”。当前节点是“局部中心节点”，还是“边缘节点”，亦或是“连接性节点”，其生成的序列包含的节点数量和顺序必然是不同的，从而让最终的 Embedding 抓取到更多结构性信息。

而为了表达“同质性”，随机游走要更倾向于 **DFS（Depth First Search，深度优先搜索）**才行，因为 DFS 更有可能通过多次跳转，游走到远方的节点上。但无论怎样，DFS 的游走更大概率会在一个大的集团内部进行，这就使得一个集团或者社区内部节点的 Embedding 更为相似，从而更多地表达网络的“同质性”。

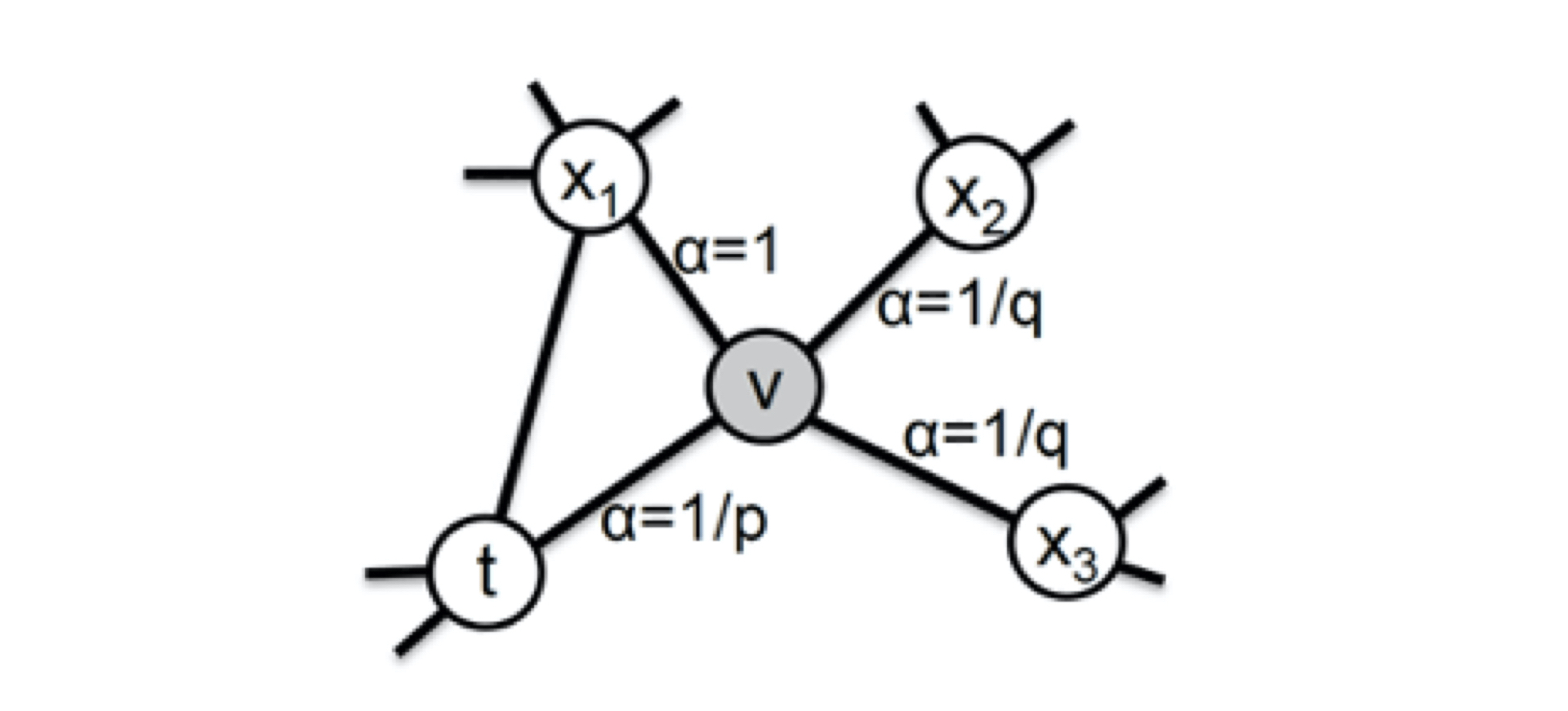
Node2Vec主要是通过节点间的跳转概率来控制跳转的倾向性。图 6 所示为 Node2vec 算法从节点 $t$ 跳转到节点 $v$ 后，再从节点 $v$ 跳转到周围各点的跳转概率。这里，你要注意这几个节点的特点。比如，节点 $t$ 是随机游走上一步访问的节点，节点 $v$ 是当前访问的节点，节点 $x_1$、$x_2$、$x_3$是与 $v$ 相连的非 $t$ 节点，但节点 $x_1$还与节点 $t$ 相连，这些不同的特点决定了随机游走时下一次跳转的概率。

图6 Node2vec的跳转概率

这些概率我们还可以用具体的公式来表示，从当前节点 $v$ 跳转到下一个节点 $x$ 的概率 $\pi vx​=\alpha _{pq}​(t,x)\cdot \omega _{vx}​$ ，其中 $\omega _{vx}​$ 是边 $vx$ 的原始权重，$\alpha _{pq}​(t,x)$ 是 Node2vec 定义的一个跳转权重。到底是倾向于 DFS 还是 BFS，主要就与这个跳转权重$\alpha _{pq}​(t,x)$的定义有关了：

$\alpha_{p q(t, x)=}\left{\begin{array}{cc}\frac{1}{p} & \text { 如果 } d_{t x}=0 \ 1 & \text { 如果 } d_{t x}=1 \ \frac{1}{q} & \text { 如果 } d_{t x}=2\end{array}\right.$

$\alpha _{pq}​(t,x)$ 中的参数 $p$ 和 $q$ 共同控制着随机游走的倾向性。参数 $p$ 被称为返回参数（Return Parameter），$p$ 越小，随机游走回节点 $t$ 的可能性越大，Node2vec 就更注重表达网络的结构性。参数 $q$ 被称为进出参数（In-out Parameter），$q$ 越小，随机游走到远方节点的可能性越大，Node2vec 更注重表达网络的同质性。反之，当前节点更可能在附近节点游走。

1.4 通过Word2Vec构造词嵌入向量

用户在浏览商品时，存在浏览相似商品的行为，我们可以利用这一特性对不同商品间的相似性进行建模。而Word2Vec可以对序列数据进行无监督学习，可以满足我们的需求。

在当前场景下，商品有brand_id和cat_id两个特征，即品牌ID和类别ID。我们可以用Word2Vec将这两个类别变量转化为低维连续变量，并根据用户历史记录中用户或商铺对brand_id和cat_id的权重对其进行加权平均，得到新的用户隐向量和商铺隐向量，丰富了特征信息。

举例，用户按时间顺序访问了以下5个商品：

item_id	cat_id	brand_id
1	A	a
2	B	b
3	B	c
4	A	a
5	A	a

对于这些商品的cat_id，我们可以得到一个序列：

[A, B, B, A, A]

假设我们用Word2Vec对cat_id序列了3维的隐向量（词嵌入向量），如下：

cat_id	dim-1	dim-2	dim-3
A	0	1	0.5
B	1	0	0.5

假如用户U1曾访问过75次cat_id = A的商品，访问过25次cat_id = B的商品，那么可以用加权平均算得U1的隐向量如下：

user_id	dim-1	dim-2	dim-3
U1	0.25	0.75	0.5

同理可以计算商铺的隐向量。

通过以上方式，我们从新的角度对用户和商铺进行了编码，引入了新的特征。

1.5 boruta特征筛选

2. 模型训练与模型融合

参考资料

【Graph Embedding】node2vec：算法原理，实现和应用

Alias Method:时间复杂度O(1)的离散采样方法

【数学】时间复杂度O(1)的离散采样算法—— Alias method/别名采样方法

07 | Embedding进阶：如何利用图结构数据生成Graph Embedding？