Visualizing concepts is a great way to learn them. It is also a great way to teach them. Vizcal is a tool to help you visualize Calculus concepts. Find visualization tools for Limits, Derivatives, Riemman Sums, and Arc Length. Made using Electron, Vite, and React - see evite.
This functionality is useful when the user wants to open a file that they have previously saved on their device. By clicking on the "load an existing experiment from a file" text, the user can navigate through their device and select the file they want to open.
This functionality allows the user to adjust various parameters in each experiment.Each parameter is specific to its experiment.
This functionality allows the user to switch between two different visual themes in the application. This includes light and dark modes.
This functionality allows the user to customize the colors used in the application. For example, they are able to change the color of the graph's function.
This functionality allows the user to adjust the font used throughout the application.
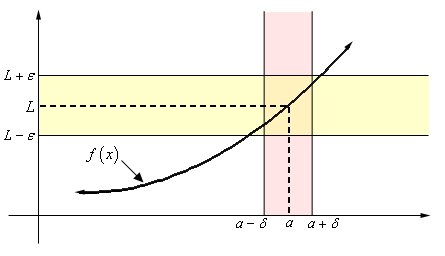
A limit is a fundamental concept in calculus and mathematical analysis that describes the behavior of a function as its input approaches a particular value. In other words, it is the value that a function approaches as the input gets arbitrarily close to a specific point. Limits are used to define the concepts of continuity, derivatives, and integrals in calculus.
The derivative of a function at a given point is the instaneous slope of said function at said point. The values for the run and rise dictate the range of points at which the derivative is calculated and then yields the average slope of the function between these points.
In mathematics, a Riemann sum is a certain kind of approximation of an integral by a finite sum. Riemann sums help us approximate definite integrals, but they also help us formally define definite integrals. Through Rieman sums, we give the answer to a problem with an approximation, refine it to make it more precice, and use limits to obtain an exact answer. This application focuses on the two first parts of the process.
The arc length is an application of integration that lets us find the length of a function within a certain range. The method by which this is achieved is very similar to the approximation of the area under a curve where Riemann sums where exhaustively used. In short, subdivisions in x of a function are joined by straight lines and they are all joined to approximate the curve of the function. The approximation is simply given by the sum of the length of each small line section.
.
├──src # Electron
│ ├──main
│ │ └──index.js
│ ├──preload
│ │ └──index.js
│ └──renderer # React
│ ├──src
│ │ ├──assets
│ │ ├──components
│ │ └──hooks
│ ├──index.html
│ └──...
├──electron.vite.config.js
├──package.json
└──...$ npm install$ npm run dev$ npm run test# For windows
$ npm run build:win
# For macOS
$ npm run build:mac
# For Linux
$ npm run build:linux